A Fuzzy Adaptive Algorithm Based on“Current”Statistical Model for Maneuvering Target Tracking
2010-07-25WANGXianghua王向华QINZheng覃征YANGHuijie杨慧杰YANGXinyu杨新宇
WANG Xiang-hua(王向华),QIN Zheng(覃征),YANG Hui-jie(杨慧杰),YANG Xin-yu(杨新宇)
(1.Department of Computer Science and Technology,Tsinghua University,Beijing 100084,China;2.Department of Computer Science and Technology,Xi'an Jiaotong University,Xi'an 710049 Shaanxi,China)
Introduction
The building of movement model is a hot and difficult problem in the field of maneuvering target track,and some researchers have done much work deeply and widely.The“current”statistical model and adaptive tracking algorithm[1]presented by Chinese researcher ZHOU Hong-ren is an effective method for tracking a maneuvering target.However,since the“current”statistical model has a design limitation,the adaptive tracking algorithm can achieve good track result for strongly maneuvering target,but can't give an ideal track result for weakly maneuvering target.In order to solve this problem,many researchers have conducted many attempts,the introduction of fuzzy control theory is a feasible approach[2-3].But,a catastrophe exists in the triangular membership function,which can bring the expense of tracking precision.In the paper,the basic characters of“current”statistical model and adaptive Kalman filter algorithm(CSAF)was analyzed,a nonlinear exponent form fuzzy control membership function without catastrophe was designed to correct the problem in the model,and a novel“current”statistical model-based fuzzy adaptive algorithm was presented to improve the tracking precision for weakly maneuvering target.The computer simulation proved the validity of new algorithm.
1 “Current” Statistical Model and Adaptive Tracking Algorithm
The basic idea of CSAF is to describe the statistic characteristics of target acceleration via amended Rayleigh distribution.When the“current”acceleration of target is positive,its probability density function is
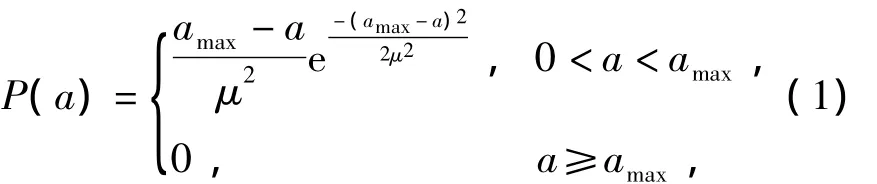
whereamaxis the upper limit of target acceleration,amax>0,ais the target random acceleration,μis a constant(μ>0).The mean and variance ofaare given by

When the“current”acceleration of target is negative,its probability density function is

whereamax(amax<0)is the lower limit of target acceleration.The mean and variance of random acceleration are given by

In particular,while the“current”acceleration of target is 0,its probability density function is

whereδ(·)is Dirac function.
The discrete time state equation for“current”statistical model of maneuvering target is given by

whereX(k+1)is system state vector,including position,velocity and acceleration components,Φ(k+1,k)is state transition matrix,U(k)is input matrix,a(k)is the average value of“current”acceleration,W(k)is discrete time white noise,and
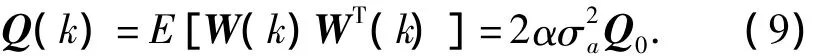
The calculation method aboutΦ(k+1,k),U(k)andQ0is given in detail in Ref.[1].The unnecessary details will not be given here.
The measurement equation is
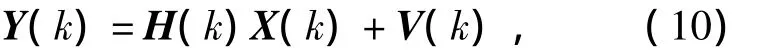
whereH(k)is observation matrix[1,0,0],V(k)is Gauss white noise with mean 0 and varianceR(k).
The adaptive Kalman filter equations based on state Eq.(8)and measurement Eq.(10)are

The adaptability of the algorithm is to adjustwith the change of“current”acceleration.Therefore,the state noise covariance matrixQcan be adjusted adaptively.
When the“current”acceleration is positive,

When the“current”acceleration is negative,
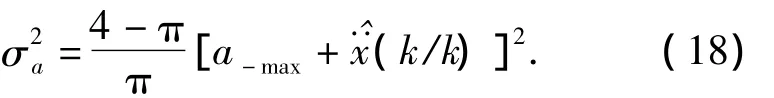
However,the“current”statistical model and the adaptive Kalman filter algorithm have the design limitations.In other words,the algorithm can track strong maneuvering target effectively,but the results are bad while tracking weak maneuvering target,because the“current”statistical model can't describe this type of target[4].
When the “current” acceleration is positive,based on Eq.(1)and random process theory,we can obtain
When Eq.(5)is substituted into Eq.(19),the range ofμis obtained

In a similar way,when the“current”acceleration is negative,according to Eq.(4),(5)and(6),we can get

Then,Eq.(20)and(21)are substituted into Eq.(2)and(5),respectively,we have


2 Description of FACS Algorithm
Although some researchers presented some adaptive algorithm[5-6]based on fuzzy membership function,the triangular membership function is commonly used,as shown in Fig.1.This function makes system noise estimation break when the membership grade changes,resulting in a big error.

Fig.1 Triangular membership function
In this paper,an exponential nonlinear fuzzy membership function was designed,which don't bring adjusting break,and can be used to track weak maneuvering target effectively.On the assumption that the range of target acceleration is[a-up,aup],two thresholds,athanda-th,are given in our algorithm,andath>aup,a-th<a-up,the expression of fuzzy membership functionMis
wherek1andk2are constants,of which values are restricted by the following conditions:
for∀a(0≤a≤aup),

for∀a(a-up≤a<0),

Figure 2 shows the fuzzy membership function and the values ofath,a-th,aupanda-up.
By combining Eq(24),(25)and(26),we have


Fig.2 Nonlinear exponential membership function
In the“current”statistical model,acceleration upper and lower limits change adaptively withM,namely,


In fact,our FACS algorithm is adaptively to control and adjust the parametersamaxanda-maxin the“current”statistical model through target maneuvering state, namely real-time acceleration, enabling the“current”statistical model to adapt to any movement state of target.And then,the tracking precision can be improved by running a relevant adaptive Kalman filter algorithm.
3 Simulation and Analysis
In simulation experiment,FACS parameters were assigned as follows:ath=100 m/s2,a-th= -100 m/s2,aup=90 m/s2,a-up= -90 m/s2,k1=k2=0.97.The basic“current”statistical model and the adaptive Kalman filter algorithm(CSAF)were used in the comparing experiments,andamax=90 m/s2anda-max= -90 m/s2.
The quality of state estimation[7]is used to evaluate the experimental results.The quality of state estimation is described by root-mean-square error(RMSE).The expression ofRMSEis
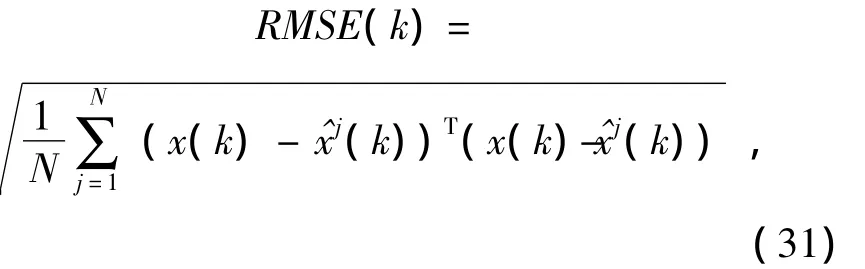
whereNis the times of Monte Carlo simulation,jrepresents thejth simulation,x(k)and^xj(k)represent the real value and filter estimated value of the target state at timek,respectively.
3.1 Tracking Experiment of Velocity Maneuvering Target
In this group of experiments,we proved the validity of FACS algorithm for velocity maneuvering target by tracking a target of variable-velocity linear motion.The simulation lasted 200 s,the sampling periodTwas 1 s.Let it be supposed that the initial position of target was at 10 km,and its initial velocity was 100 m/s.The acceleration was 30 m/s2in 1-50 sampling periods;it was changed to 20 m/s2in 51-100 sampling periods;it continued to be reduced to 10 m/s2in 101-150 sampling periods;and it was reduced to 5 m/s2in 151-200 sampling periods.
The Monte Carlo simulation results from 100 experiments are given in Fig.3,4 and 5,which show RMSE of position,velocity and acceleration,respectively.

Fig.3 Comparison of position RMSE

Fig.4 Comparison of velocity RMSE
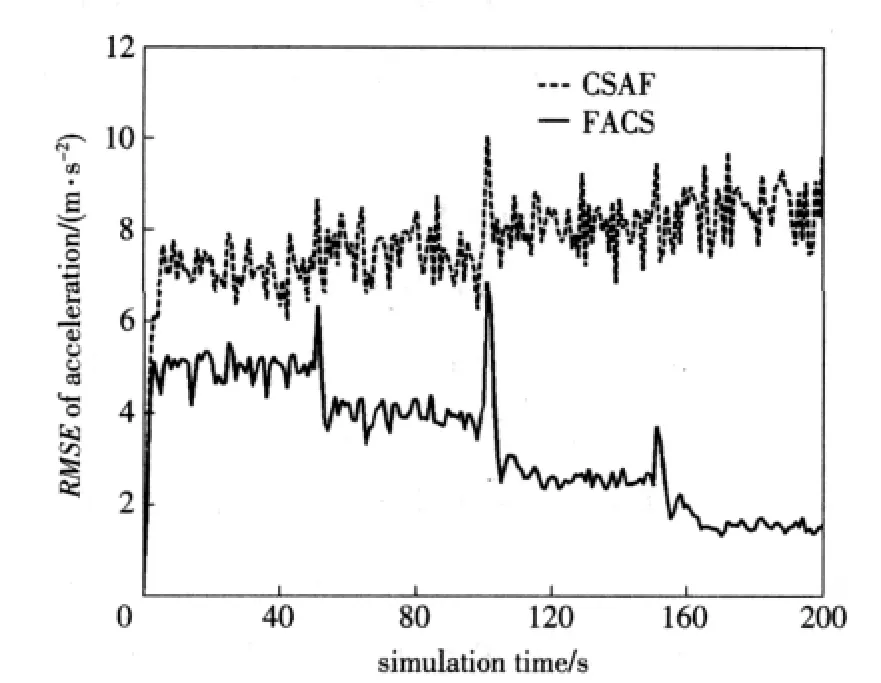
Fig.5 Comparison of acceleration RMSE
It can be seen from the simulation results that our FACS achieved better precision than the basic“current”statistical model and adaptive Kalman filter algorithm in RMSE of position,velocity and acceleration by adjustingamaxanda-maxadaptively according to target real-time acceleration.In particular,FACS algorithm has an obvious advantage over the CSAF algorithm for the weak maneuvering target.When the maneuvering acceleration of target is small,the basic“current”statistical model can't describe this maneuvering state because the acceleration upper limit is too large and the lower limit is too small.However,our FACS algorithm can adjust the acceleration upper and lower limits in real-time according the maneuvering state of target,and describe the state of weak maneuvering target effectively.Therefore,its tracking error is much smaller than that of CSAF algorithm.
FACS algorithm improves tracking performance at the expense of a little increased amount of computation,but can't lead to any significant impact on its real-time application.The simulation programsof CSAF and FACS were run on the same computer,the average values of running time are shown in Table 1.The average time is increased by 7%.

Table 1 Runtime comparison of two algorithms
3.2 Experiment of Target Track Maneuvering
In this group of experiments,FACS algorithm was used to track a track maneuvering target.The simulation time lasted 150 s,the sampling periodTwas 1 s.Supposed that the initial position was(10 km,0),the initial velocity was(150 m/s,0).In the period of 1 -30 s,the target moved at constant velocity;in the period of 31-150 s,it moved at uniform circular motion with radius 10 km,as shown in Fig.6.

Fig.6 Moving track of target
The experimental results were obtained after 100 Monte Carlo simulations.Fig.7 shows the RMSE of position for tracking target.It is obvious that the performance of FACS is better than that of basic“current”statistical model and adaptive tracking algorithm.
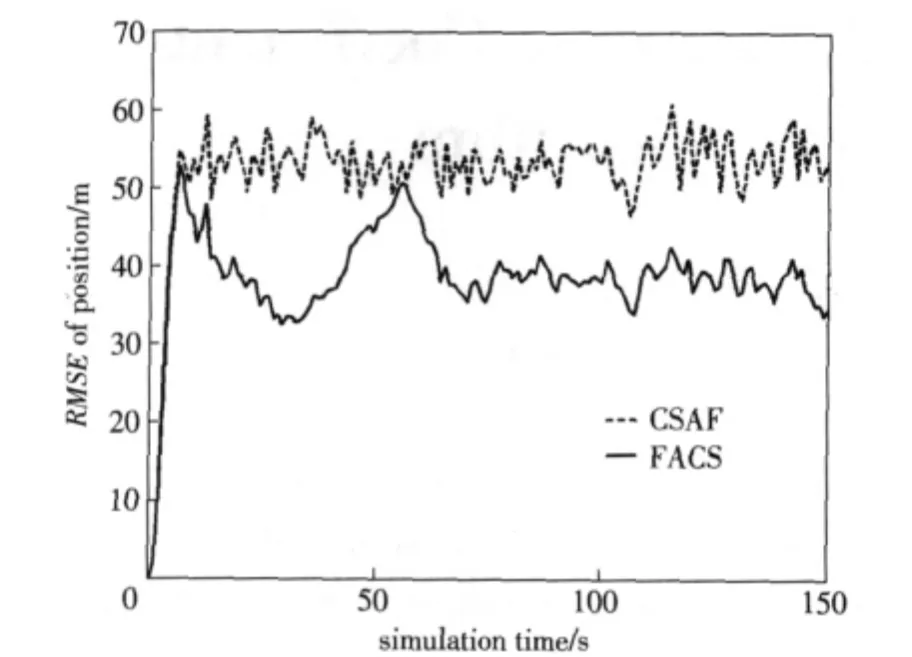
Fig.7 Comparison of position RMSE
4 Conclusions
The basic theory and process of the“current”statistical model and adaptive Kalman filter algorithm for maneuvering target tracking were given,and the problems in this model and algorithm were analyzed theoretically.Then,by combining with fuzzy control theory,a smooth nonlinear exponential fuzzy membership function was used to adjust the acceleration upper and lower limits adaptively so that the tracking precision was improved.At last,the validity of FACS was proven through computer simulation experiments.
[1]ZHOU Hong-ren,JING Zhong-liang,WANG Pei-de.Maneuvering target tracking[M].Beijing:National Defence Industry Press,1991:134-144.(in Chinese)
[2]HU Cong-wei,CHEN Wu.Adaptive Kalman filtering for vehicle navigation[J].Journal of Global Positioning System,2003,2(1):227-233.
[3]Al-Dhaher A G H,Mackesy D.Multi-sensor data fusion architecture[C]∥ The 3rd IEEE International Workshop on Haptic,Audio and Visual Environments and Their Applications,USA:IEEE,2004:159 -163.
[4]DIAO Lian-wang,YANG Jing-yu.An improved description of“current”statistical model for maneuvering target[J].Journal of China Ordnance,2005,26(6):825 -828.(in Chinese)
[5]Abdolreza D T,Nasser S.Novel adaptive Kalman filtering and fuzzy track fusion approach for real time application[C]∥The 3rd IEEE Conference on Industrial Electronics and Applications,USA:IEEE,2008:120 -125.
[6]BA Hong-xin,ZHAO Zong-gui,YANG Fei,et al.Fuzzy adaptive tracking algorithm for maneuvering target[J].Journal of System Simulation,2002,16(6):1181 -1183.(in Chinese)
[7]RONG Li X,ZHI Xiao-rong,ZHANG You-min.Mutiplemodel estimation with variable structure partⅢ:modelgroup switching algorithm[J].IEEE Transactions on Aerospace and Electronic Systems,2003,35(1):225 -241.
杂志排行
Defence Technology的其它文章
- Analysis on Velocity Characteristics of Cavitation Flow Around Hydrofoil
- Influence of Accelerated Aging on Detonation Performance of Explosives
- Research on Additional Loss of Guidance Optical Fiber
- An HLA/RTI Architecture Based on Multi-thread Processing
- Beam Pattern Synthesis Based on Hybrid Optimization Algorithm
- Robust Stability Criterion for Uncertain Neural Networks with Time Delays
