基于双置乱与奇异值分解的彩色图像水印算法
2010-03-06石红芹吕方亮
石红芹,吕方亮
(华东交通大学 软件学院,江西 南昌 330013)
数字水印是信息安全的重要组成部分,作为数字产品认证和版权保护的重要手段,已得到越来越多的关注和发展。数字水印应具有以下几个基本特性:(1)不易察觉性:数字产品引入数字水印后,应不易被接收者察觉,同时又不能影响原作品的质量。(2)鲁棒性:能在多种无意或有意的信号处理过程后产生一定的失真,但仍保持水印完整性和鉴别的准确性。(3)水印容量:嵌入宿主图像水印的多少,将直接影响图像的不可见性。数字水印的不易察觉性与鲁棒性是相互矛盾的,解决这矛盾的有效途径是充分利用人类视觉系统的掩蔽特性。目前在灰度图像中嵌入数字水印受到了广泛深入的研究,并且形成了产品[1]。但在实际应用中,彩色图像和视频占主导地位。因此,近年来人们的研究兴趣逐渐转向在彩色图像和视频中嵌入数字水印。文献[2]提出了一种基于SVD的水印算法,虽然其对抗常规的信号处理攻击鲁棒性较高,但是利用伪造攻击[3]对该算法进行攻击能使算法失去意义。本文利用水印和载体图像双双置乱,进一步消除了像素之间的相关性且提高了水印信息的安全性。水印嵌入到奇异值中能对原始图像的剪切、旋转、行列镜像等几何攻击具有比较好的稳健性。
根据HVS水印策略,人眼对YUV彩色空间中亮度分量Y的敏感性低于RGB彩色空间中各个颜色分量的敏感性,这样将水印信息嵌入到Y分量中具有较高的鲁棒性。因为一般的彩色图像都是用RGB彩色空间来表示,所以首先要将彩色图像由RGB模式转换到YUV模式以得到亮度Y分量。YUV彩色空间与RGB空间的转换关系式(1)

Y表示亮度,U,V用来表示色差,R,G,B分别表示红色、绿色、蓝色分量值。
1 图像置乱
图像置乱作为一种图像加密技术,成为数字图像加密的重要手段之一。所谓图像置乱技术是指将一幅图像的像素的空间位置重新进行排列,将原始图像变换成杂乱无章的新图像。如果不知道所使用的置乱方法和密钥,就很难恢复出原始图像。置乱变换有两个重要特点:(1)置乱变换一般都有周期性,先是越来越乱,而后当迭代到一定次数之后就会恢复到原图。(2)置乱变换只是令像素的空间位置发生了变换,而像素的值不变。
1.1 Fibonacci变换
Fibonacci数列是数学中很重要的数列,由于它具有许多重要的应用,所以一直受到人们的青睐。Fibonacci数列的定义如下
令:F1=1,F2=1,一般地公式(2)为Fibonacci数列

Fibonacci变换的公式见(3)

Fn、Fn+1是Fibonacci数列中的两个相邻数,其中 k=0,1,2,3,…Fn+1-1;r=0,1,2,3,…Fn+1-1。这里r可作算法中密钥的一部分。由定义可以看出,该变换可将数列{Q}=(0,1,2…,Fn+1-1)变换成另一个新数列{S}=(S0,S1,S2,…SFn+1-1)且可以证明{S}是{Q}的一个伪随机置换[4]。考虑到Fibonacci变换置乱度计算量小,置乱的周期短,速度快。故而对彩色载体图像用Fibonacci变换。图1为载体图像,图2为经过Fibonacci置乱变换的载体图像。
1.2 Arnold变换
Arnold变换是将图像看作平面区域上的二元函数Z=F(x,y),(x,y)∈R,通常区域R是一个矩形。对R中的任意点相对应的函数值代表图像的信息(如灰度值等)。
图像的离散Arnold变换即为式(4)

式中:(x,y)表示该图像矩阵的某个元素未变换时的位置,(x′,y′)表示变换后新的位置。通过变换水印图像由清晰到模糊,提取水印后,可以利用Arnold变换的周期性,重新得到原图像.表1为部分不同尺寸的图像经Arnold变换的周期表:
因Arnold变换具有算法简单,运算快和具有周期性等特点故对水印的加密采用二维Arnold变换。图3为水印图像,图4为经过Arnold置乱变换的水印图像。

表1 Arnold变换的周期

图1 载体图像

图2 置乱后的载体图像

图3 水印图像图

图4 置乱后的水印图像
2 图像的奇异值分解
奇异值分解是线性代数中一种重要的矩阵分解,在信号处理、统计学等领域有重要应用。数字图像可以被视为有许多非负标量组成的矩阵,奇异值分解(singular value decomposition,SVD)是一种将矩阵进行对角化的数值技术,已被广泛应用与图像编码和其他信号处理技术中。从图像处理的角度来看,奇异值分解有如下的特性:一幅图像的奇异值具有相当好的稳定性,也就是说,当图像受到轻微的扰动时,它的奇异值不会发生剧烈的改变,从线性代数的角度来看,一幅数字图像可以看成是由一个许多非负标量项组成的矩阵。用X∈RN×N表示一个图像矩阵,其中R表示实数域,则X的奇异值分解定义如式(5)

式中:U∈RN×N和V∈RN×N均为正交阵,S∈RN×N为对角阵。其对角线上的元素满足式(6)

式中:r为X的秩,λi(1≤i≤N)由分解惟一确定,它称之为X的奇异值。图像SVD分解,其奇异值所表现的是图像内在的代数特性而非视觉特性,它可以作为图像特征之一。奇异值的稳定性非常好,当图像被施加小的扰动时,图像的奇异值不会有大的变化。文献[5]给出了SVD分解运用于水印嵌入算法的理论分析。
3 水印的嵌入与水印的提取
3.1 水印的嵌入
本文选取的载体图像为M×M的彩色图像Baboon,水印为N×N的二值图像Cameraman。因为当载体图像较大的时候进行奇异值分解的时间较长,故可先将其分块后再分别对每块进行SVD分解。具体的水印嵌入过程描述如下:
步骤1:将原始水印图像进行二维Arnold置乱得待嵌入的水印图像,迭代的次数k就是一个密钥。应用公式(7),对置乱水印图像进行奇异值分解。

其中T为共轭转置。
步骤2:将彩色载体图像由RGB模式转换为YUV模式后对Y分量进行Fibonacci置乱变换,置乱参数r可以作为密钥。
步骤3:对置乱后的载体图像进行8×8分块,对每一块进行奇异值分解,得到公式(8)

其中:j代表各个分块,λji(i=1,2,…,N)为Sj的奇异值元素。
步骤4:利用公式(9)修改各个分块的奇异值,嵌入水印图像的奇异值到各个分块中。

3.2 水印的提取
水印提取是水印嵌入的逆过程,在水印图像的加密域进行。具体提取过程如下:
步骤1:对含水印图像进行彩色空间模式变换,由RGB转换为YUV模式后进行Fibonacci置乱变换后,提取Y分量进行8×8分块。
步骤2:由公式(8)对各分块进行奇异值分解,再利用公式(11)从各分块中提取水印图像的奇异值。

其中 i=1,2,…,N,j=1,2,…,64,αj为嵌入因子。
步骤5:利用修改后的各分块的奇异值集,由公式(10)进行重构,逆Fibonacci变换,再由YUV模式转换为RGB模式,得到嵌入水印后的载体图像。

其中:i=1,2,…,n,j=1,2,…,64。
步骤3:利用公式(7),提取出置乱水印图像,再经利用Arnold反置乱技术和提供的密钥(置乱次数k和加密者的密钥)解密提取出来的信息,即得到可能已经失真的图像水印。
4 实验结果与仿真
本实验采用512×512的彩色图像Baboon,水印为128×128的二值图像Cameraman,为了客观地验证本算法的性能,这里引入两个指标:归一化相关系数NC:原始水印和提取出的水印之间的相似度可以通过相关性检验来衡量;峰值信噪比PSNR:用来客观反映图像视觉特性的指标,嵌入水印的图像可以用PSNR验证水印的不可见性。图5为水印图像受到攻击时的部分测试结果图。
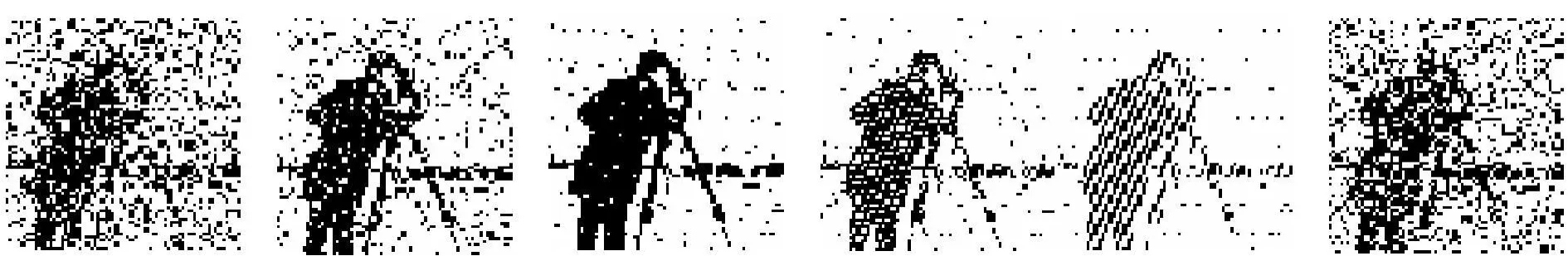
图5 水印图像部分攻击测试结果
本文算法与常用的鲁棒性较好的小波域置乱水印算法[6]和基于改进型的SVD算法[7]作比较,用水印图像常常遇到的攻击手段对无置乱、水印置乱、原图置乱和本文采用的双置乱算法进行攻击,观察它们的NC值。实验结果的比较如表2。
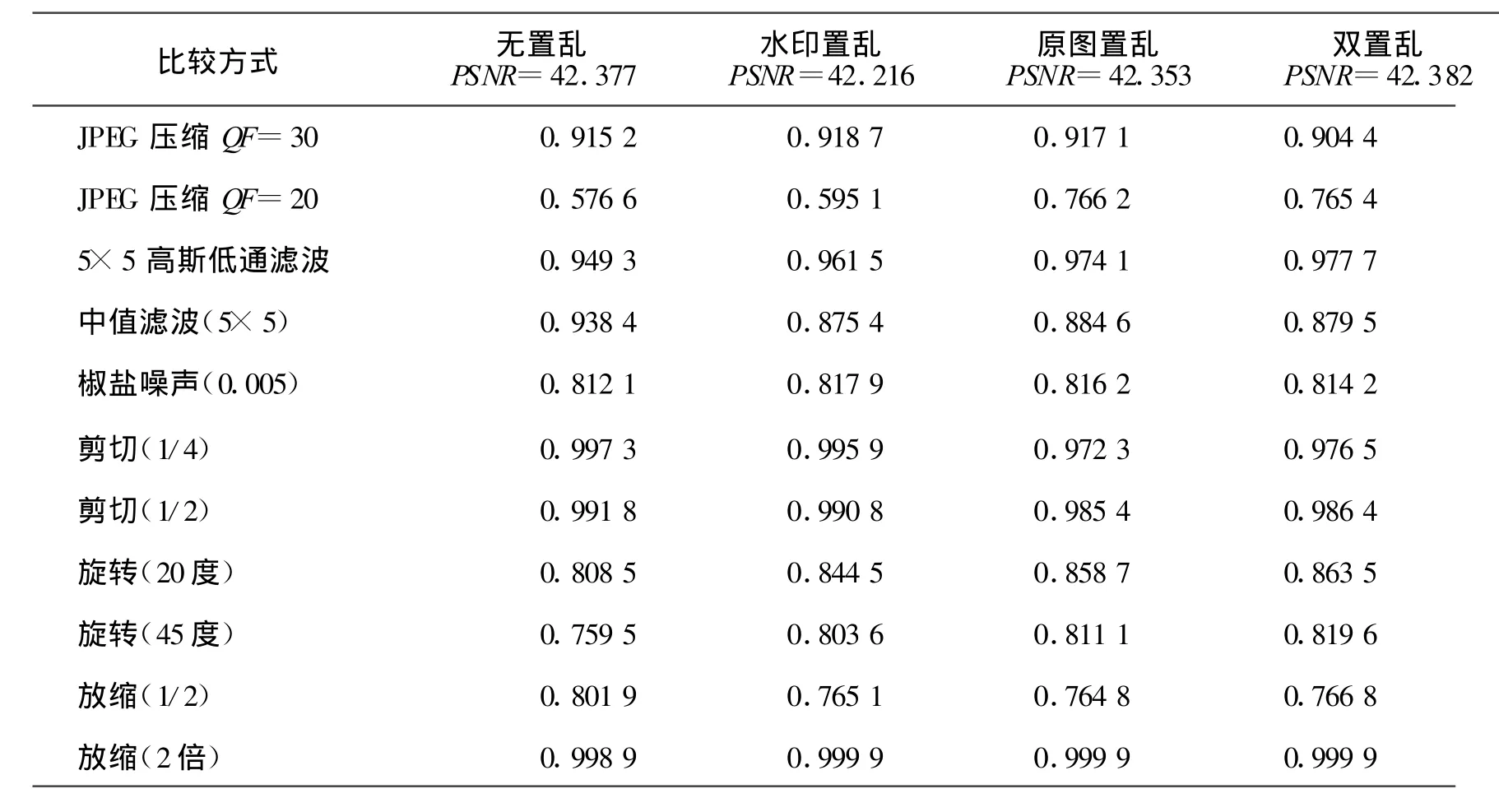
表2 不同置乱方式下的抗攻击实验NC值比较
5 结论
由以上各个实验可以看出,本文采用的水印嵌入策略,很好地满足了数字水印的不可见性,在人类视觉系统中图像明显改变的攻击下,也表现了不错的鲁棒性,本算法的创新之处就在于采用了水印和彩色载体图像的双置乱,不但较好地保证了算法的安全性,而且在抗几何变换攻击上也具有良好的性能。
[1]李斌,王新伟.关于SVD图像水印算法的分析和改进[J].华东师范大学学报,2007,13(1):100-106.
[2]王淑琴,张金海,王卫民.一种基于奇异值分解的自适应水印算法[J].计算机仿真,2008,25(8):109-112.
[3]徐超汉,柯宗贵.计算机网络安全实用技术[M].北京:电子工业出版社,2005.
[4]堪志鹏,邹建成.一种基于Fibonacci变换的视频置乱技术[J].北方工业大学学报,2007,19(3):6-10.
[5]李学斌,俞登峰,程亮.基于奇异值分解的零水印算法[J].计算机工程,2009,35(11):163-165.
[6]杨卫民,谭骏珊,金正.基于奇异值分解的彩色图像水印算法[J].计算机工程与设计,2008,29(23):6 151-6 153.
[7]张遂生,袁正道.基于奇异值分解的数字水印改进方案[J].南京师范大学学报,2008,8(4):141-144.
