概率分布中的递推问题与Panjer递推公式

2010-02-28王丙参徐长伟宋立新

河北北方学院学报（自然科学版） 2010年2期

王丙参,徐长伟,宋立新

(1.天水师范学院数学与统计学院,甘肃天水741001;2.中原工学院理学院,河南郑州450007;3.吉林师范大学数学学院,吉林四平136000)

1981年,Panjer给出了一种计算概率 f(x)的递归方法,它的前提条件是理赔额的概率分布列满足递归式,而精算领域中理赔额经常取值非负整数,即离散型随机变量.Panjer的成果发表后,类似的公式在排队论中已被推导,现在精算领域已经出现了大量的研究类似递归式的论文[1,2].因此本文利用归纳递推的思想给出了常用的离散型随机变量概率分布列的递推公式并探讨与Panjer递推公式的关系,从而更好的理解离散型随机变量及其应用.

1 离散型随机变量的递推公式

如果记 X为n重伯努利试验中事件A成功的次数,则 X的可能取值为0,1,…,n,记 p为事件A发生的概率,则 X服从参数为(n,p)的二项分布,记为 X～B(n,p).显然当n=1时为两点分布[3,4].

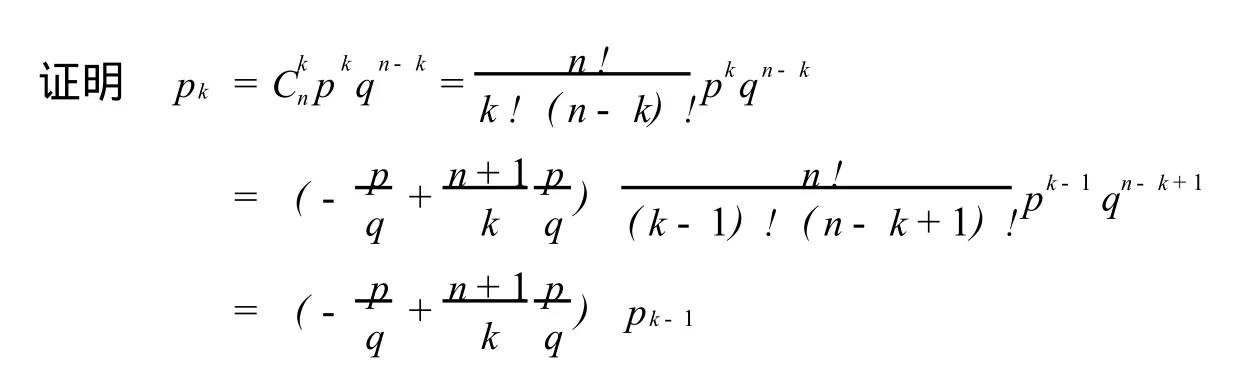
在伯努利试验序列中,记每次试验中事件A发生的概率为p,如果 X为事件A首次出现时的试验次数,则 X的可能取值为1,2,…,称 X服从参数为p的几何分布,记为 X～Ge(p).

定理1.3 随机变量 X～Ge(p),其分布列为 Pk～P(X=k)=p(1-p)k,k=1,2,….若令 a=1-p,b=0,则有 pk=(a+) pk-1,k=2,3,…,其中 p0=p.

证明 pk=p(1-p)k=(1-p)p(1-p)k-1=(1-p)pk-1,k=2,3,…

伯努利试验序列中,每次试验中事件A发生的概率为p,如果 X为事件A第r次出现时的失败试验次数,则 X的可能取值为0,1,2,…,称 X服从参数为 (r,p)的负二项分布,记为 X～NB(r,p).

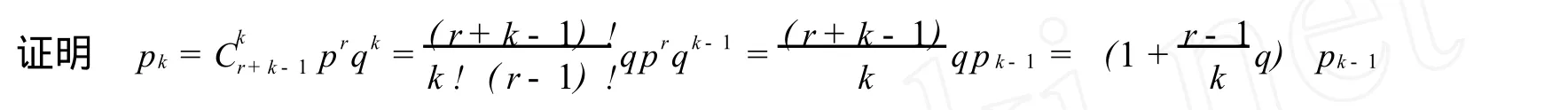
泊松分布是1837年法国数学家泊松首次提出的,它是一种重要的离散分布,常与单位时间上的计数过程相联系,譬如,在单位时间内,电话总机接到用户呼唤的次数,因此泊松分布的应用面是十分广泛的[7].

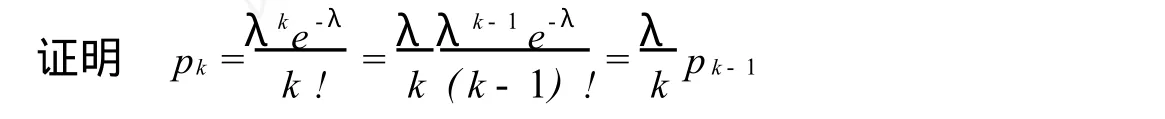
设有 N个产品,其中有M个不合格品.若从中不放回地随机抽取n个,则其中含有的不合格品的个数 X服从参数为N,M,n≤M的超几何分布,记为 X～h(n,N,M).

证明由于

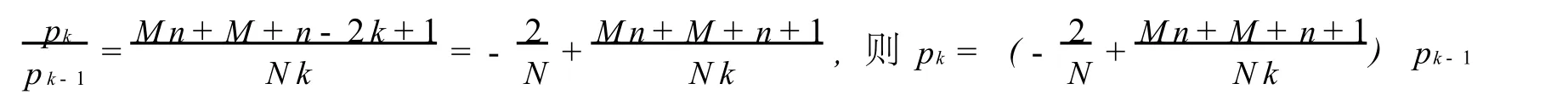
定理1.7[8]随机变量 X服从参数为p的对数分布,其分布列为2,…,其中q=1-p.若令a=1-p,b=-(1-p),则有

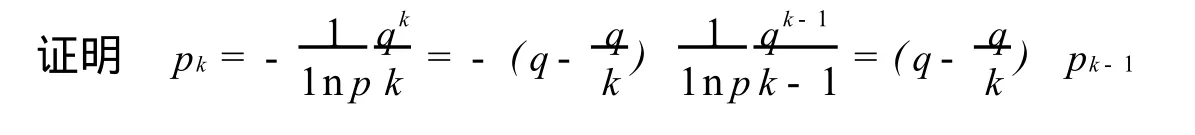
通过上面的讨论,常用的离散型随机变量的分布列pk具有规律性,即只是不同的分布中的参数a,b取值不同.

2 Panjer递推公式

设S=X1+X2+…+XN,其中 N表示理赔次数,Xi表示第i个理赔.假定理赔额 Xi是独立同分布的,N和所有Xi独立.N是一个仅取非负正整数值的随机变量,分布列为 pn=P[N=n],n=0,1,…,记mN(t) =E(etN),特别,当 N服从泊松分布时,S具有复合泊松分布.当 N服从负二项分布时,S具有复合负二项分布.聚合模型的理赔总额就是一个复合分布,因此研究复合分布具有重要的现实意义.

定理2.1 考虑这样的一个复合分布,其中理赔额取非负整数值,具有概率分布函数为 p(x),x=0,1,2,…,而且事件“有 n个理赔发生”的概率qn满足递归式…,其中a,b∈R,于是事件“理赔总额等于s”的概率满足如下关系式: