两介质接触面剪切力学行为试验与数值分析

刘晋艳,刘天亮

(1.山西大学工程学院,山西太原 030013;2.山西省交通规划勘察设计院,山西太原 030012)

对重力坝坝基稳定、岩石锚固、桥梁锚碇等问题,混凝土—岩石构成的接触面的力学行为直接影响着地质体和工程体的相互作用[1]。近年来,研究人员希望探究界面粘结力与界面起伏形貌共同作用对界面两侧应力应变场分布乃至峰值剪应力的影响。

光弹性贴片试验是揭示界面应力、应变场的方法。文献[2,3]曾用透射式光弹法刻画了具有不同粗糙度的分形节理模型接触面区域的应变场分布,文献[4～6]采用光弹性贴片的方法进行混凝土的裂纹扩展等方面的研究。有限元数值模拟也能揭示界面应力应变场分布[7～9],文献[9]通过压剪光贴片试验证实了应力集中程度随起伏角个数 m值的增加,低强度介质与高强度介质的强度之比k值[10]的增加而加强,并证明数值模拟能较好地吻合光贴片试验结果。但由于试件数量有限,对于起伏数 m增大到一定程度以至于起伏变为高频的粗糙细节成分时,其增加对应力集中程度和峰值剪应力τp的影响未作深入探讨。

因此,本文采用数值模拟方法进一步分析了m值和k值对应力集中程度和峰值剪应力τp的影响,并通过加载初期光贴片试验和数值模拟的相互吻合,揭示了采用光贴片试验和数值模拟结合的手段来分析接触面的应力集中现象具有优势。

1 试验和数值模拟方案

1.1 光贴片试验原理

用光贴片法测定结构表面应力,是通过紧贴在结构件表面上的光敏贴片,在偏振光照射下产生的双折射效应进行分析来实现的。在载荷作用下,结构件表面的应变全部传递给贴片,于是贴片所产生的效应,便完全反映了结构物表面的应变状态。用反射式光弹仪,可以在偏振镜后观察到因应变引起的双折射干涉条纹,这种条纹即是应变分布场,从而可通过应力光学定律对所测区域进行应力应变分析。

1.2 试验方案

试件制成100 mm×100 mm×100 mm的立方体,以高度中线为界,下部为混凝土,上部为砂浆,界面为宽度方向一致的规则起伏(圆弧、角),起伏数分别为4、5、6共3种。图1仅列出起伏数为4的试件,其余从略。

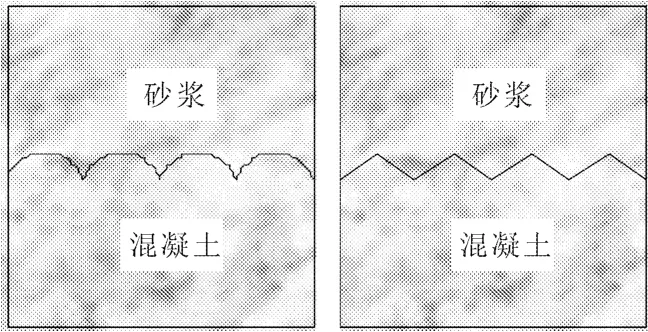
图1 试件界面形貌

试件加工好后,在侧面镀一层较薄的反光层,再将加工好的聚碳酸脂光弹贴片采用专用胶粘剂粘于反光层之上,一体的贴片与试件等大小,两体的贴片分上下两块,且形状分别与上下体重合。粘好后保证光弹性贴片与试件表面能共同变形,因而试件表面的应变可以通过贴片再现出来。

试件在模拟剪切仪[11](图2a)下平稳加载,记录接触界面处的切向位移和法向位移,同时用反射式光弹仪(图2b)测量不同荷载时特定点以及主应变差最大点处的等差线条纹级次。

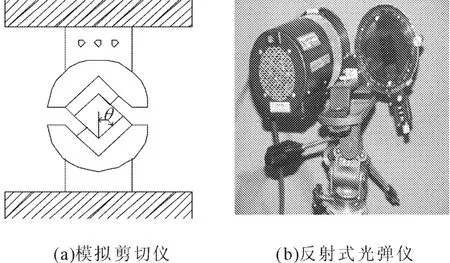
图2 模拟剪切仪和反射式光弹仪

1.3 模拟方案

数值模拟采用ANSYS软件。建模时,对100 mm×100 mm×100 mm的立方体模型,选用Concrete材料模型,根据试验条件确定的边界约束及加载方式。采用三维接触面单元Targe170和Conta174形成接触对,并引入Solid65三维实体单元。考虑到接触面处应力集中现象比较严重,应力和变形梯度较大,因而在此区域内网格划分较密[7,8]。为了探讨m值和k值对应力集中程度和峰值剪应力τp的影响,模拟时对100 mm×100 mm×100 mm的立方体模型,m值分别取4、5、6、7、8、9、10,k 值分别取 0.17、0.33、0.5、0.67、0.83、1。

2 试验和数值模拟对比

2.1 m值、k值对应力集中程度的影响

光贴片试验得到的主应变差最大点的等差线条纹级次见表1。

根据光贴片试验应力—光学定律[12]:

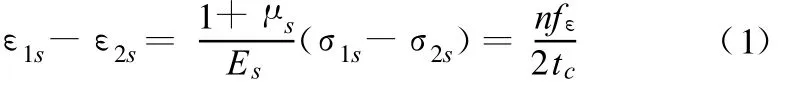
式中,n为测点处的条纹级次;fε为贴片材料的应变条纹值,单位是cm/条;tc为贴片厚度。由于试验中参数fε和tc均为常数,因此数值模拟中主应变差ε1-ε3和试验中的条纹级数n均可作为判断应力集中的依据。

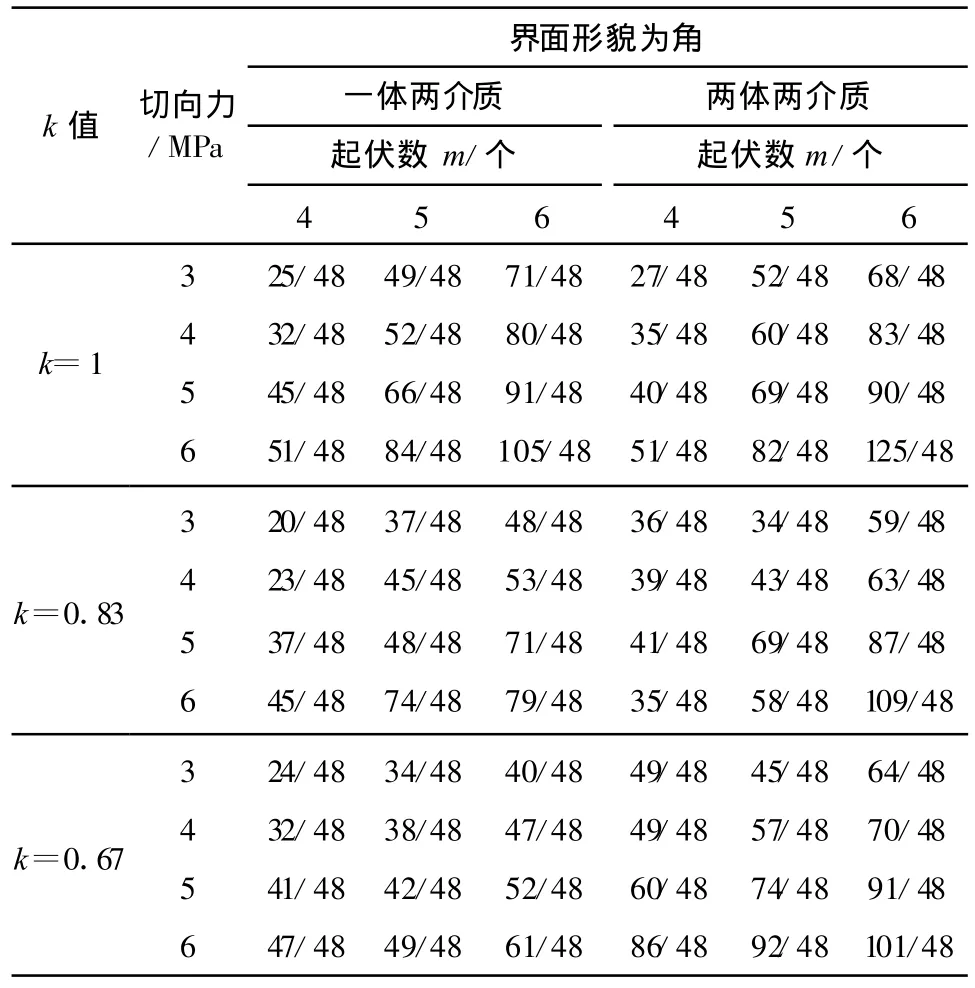
表1 等差线级次表 (单位:条)

图3是数值模拟得到的起伏数m值对主应变差ε1-ε3的影响规律。图3(a)是由加载全过程主应变差ε1-ε3的变化规律图3(b)中截取前三个点而得。可见,加载初期,主应变差ε1-ε3随着起伏数m的增大而增大,这与试验结果表1描述的趋势一致。但在加载后期材料进入非线性阶段时,起伏数m为4到8的模型与加载初期呈现相反的规律,即主应变差ε1-ε3随着起伏数m的减小而增大。

由于主应变差与应力集中直接相关,而应力集中程度越高的模型越易出现破坏,因此试验和模拟结果对比说明,虽然在加载初期起伏数 m值较大的试件应力集中程度更高,但是在起伏数m在4到8的范围内,较多的起伏仍能提供较强的抗剪切性能。在加载后期,起伏数m为9和10的模型应力集中反常地高于起伏数为6、7、8的模型,即前两者更易发生破坏,这表明,起伏数m的增长对抗剪切性能的贡献是有限的,当起伏数过多以至成为表面的粗糙细节时,其增长对试件抗剪性能的贡献逐渐减弱。

值得说明的是,光贴片试验到加载后期,应变变化剧烈,以至很难读取等差线条纹级次,因此,试验只得到弹性范围内的等差线条纹值,并且数值模拟(图3)和试验结果(表1)吻合较好。

图4是数值模拟得到的强度比k值对主应变差ε1-ε3的影响规律。由图4(a)可见,加载初期,应力集中程度随k值的增加而增大,这与试验结果(表1)吻合较好。k值越大意味着两种介质的材料强度越接近,因此在剪切荷载作用下,两者更易发生相对爬坡而不是一侧介质被剪断,这种相对的爬坡造成明显的应变和位移,从而导致应力集中加大。加载后期,随着剪切荷载的加大同时又有法向荷载的作用,两介质的相对爬坡不能无限进行,这时弱介质一侧材料必然发生破坏,破坏之前也必然伴随明显的应力集中,这时k值较小的模型反而有较高应力集中(图4b),从而也可以看出k值较大的模型可以提供更好的抗剪切性能。

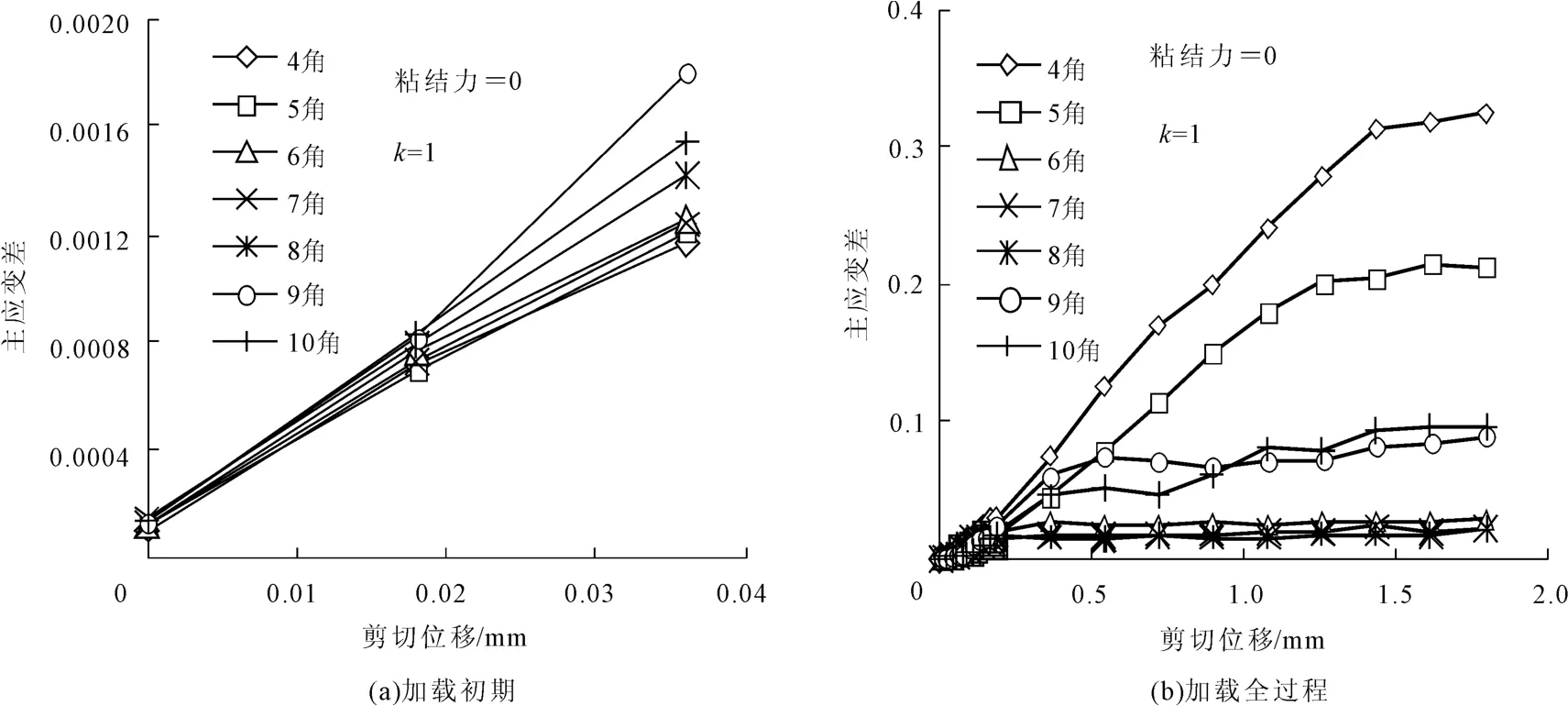
图3 剪切位移与主应变差的关系(m值的影响)

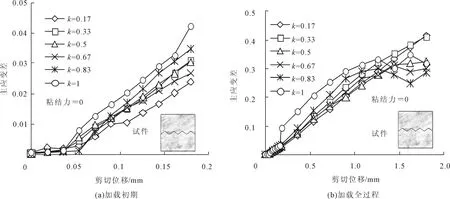
图4 剪切位移与主应变差的关系(m值的影响)

对照分析,光贴片试验和数值模拟结果在加载初期吻合较好,到了加载后期,应变剧烈,条纹级次难以捕捉,因此,光贴片试验在描述接触面应力应变场分布时仅适用于弹性阶段,当材料进入非线性阶段后,数值模拟手段较为实用。

2.2 m值、k值对峰值剪应力τp的影响

图5是试验得到的剪切位移曲线,可见,m值从4到6变化时,曲线的峰值剪应力τp随着起伏数 m值的增加而增大。

数值模拟同样可以得到试件的剪切位移曲线,提取不同m值的峰值剪应力τp得到图6。可见,m值从4到8变化时,试验和模拟结果一致。但是当 m≥9时,试件的峰值剪应力τp随着起伏数m值的增加反而呈现减小的趋势,这和图3(b)描述的应力集中现象吻合。将界面起伏数m值增大到 11、12、14、16、20、30、40、50、60、70、80、90、100 分别进行数值模拟,进一步证实了文献[9]的推测,即峰值剪应力τp不会随起伏数m的增加而无限增大。当起伏数m过多以至成为表面的粗糙细节时,其增加不能有效提高界面峰值剪应力,因此不能靠无限增加起伏角个数来提高界面抗剪性能。

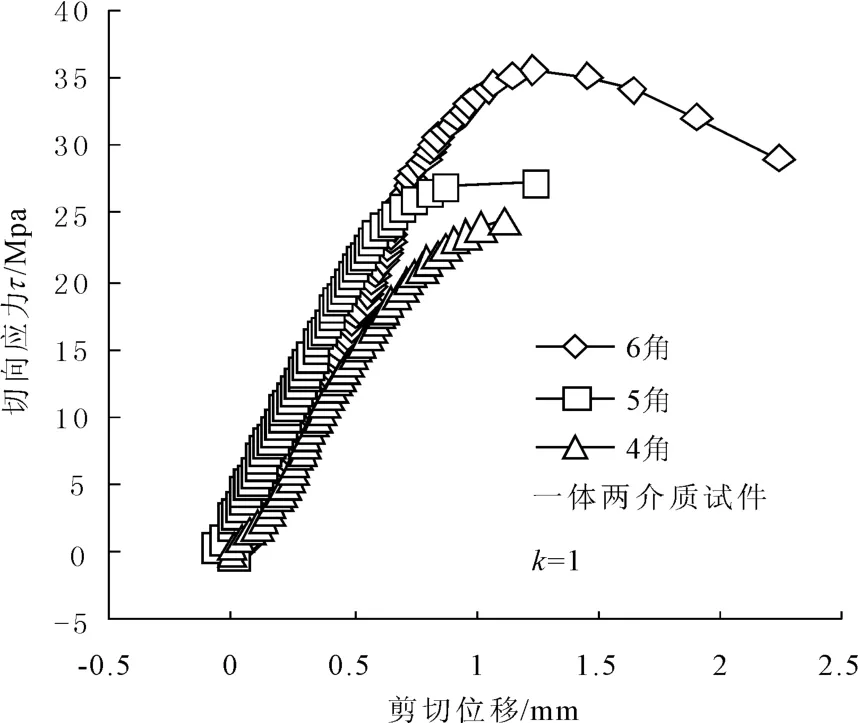
图5 起伏数m对剪切位移曲线的影响

试验证实峰值剪应力τp随着k值的增加呈近似的线性增长趋势[9],见图7。数值模拟结果(图8)对其进行了很好的吻合。这说明提高k值是增强两介质试件剪切性能的有效手段,这也和图4(b)中加载后期的应力集中随k值的变化吻合。

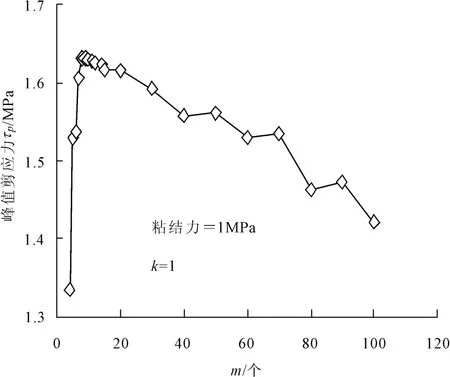
图6 起伏数m与峰值剪应力的关系

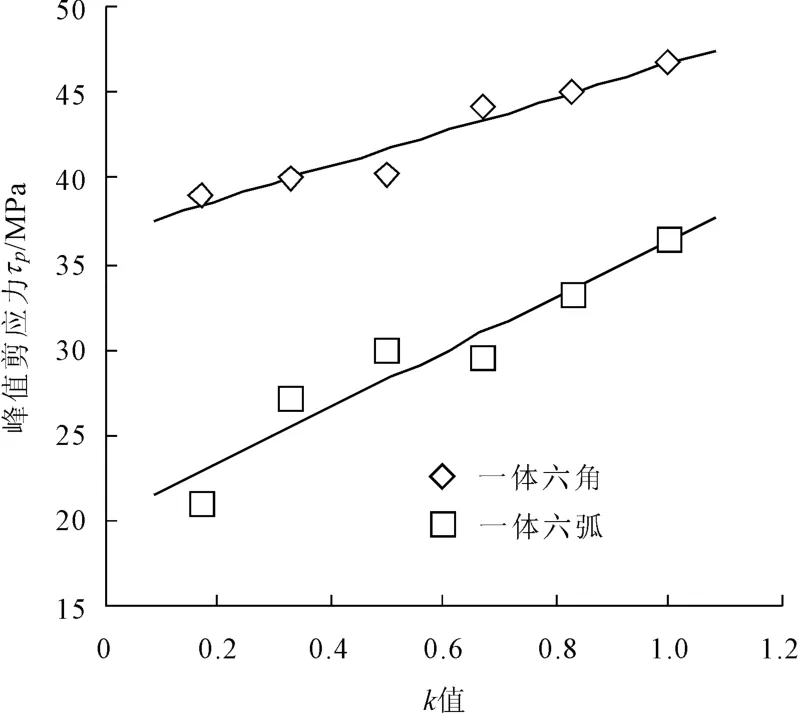
图7 k值与峰值剪应力τp的关系曲线(试验)

图8 k值与峰值剪应力τp的关系曲线(模拟)

另外,考虑到加载时法向力σ对峰值剪应力τp有重要影响,本文对粘结力为2 MPa的m=4试件进行数值模拟,并拟合得到峰值剪应力τp随两介质强度比k值和法向力σ的变化关系:

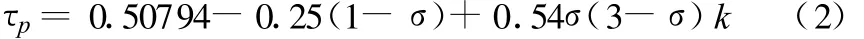
分别将 σ=0.4 MPa、0.6 MPa、0.8 MPa、1 MPa代入式(2),均可以得到,峰值剪应力τ随强度比k值呈线性增长的趋势。将代入后得到的直线绘于图8中,可见公式(2)的拟合效果较好。

3 结 论

(1)试验和数值模拟结果表明,应力集中程度与“界面起伏数 m”、“上下体材料强度比 k值”有关,在加载初期,应力集中随m值和k值的增大而增强,这与光贴片试验得到的等差线分布趋势一致,但是到加载后期,应力集中随这两个参数的变化呈现相反的规律。由于光贴片试验到了加载后期,应变变化剧烈,无法测得等差线条纹级次,因此,光贴片试验对加载后期应变场分布的描述存在缺陷。由此,本文认为采用光贴片试验和数值模拟结合的手段来分析接触面的应力集中现象具有优势。

(2)对于100 mm×100 mm×100 mm的界面形貌为角的试件,在 m≤8时,峰值剪应力τp随着起伏数m的增加而增大,当m＞8时,可以认为起伏数m已经过大称为高频粗糙细节,此时,起伏数的增加不能有效提高界面抗剪能力。

(3)峰值剪应力τp随着“上下体材料强度比 k值”的增加呈近似的线性增长趋势。拟合得到粘结力为2 MPa时,m=4的试件峰值剪应力τp随强度比k值和法向力σ的变化关系:

[1] 谢和平,陈忠辉,周宏伟,等.基于工程体与地质体相互作用的两体力学模型初探[J].岩石力学与与工程学报,2005,24(9):1457-1464.

[2] 巫静波,谢和平,高 峰.岩石节理剪切力学特性的光弹实验研究[J].中国矿业大学学报,2000,29(6):640-642.

[3] 谢卫红,卢爱红,李顺才,等.岩石分形节理光弹实验与数值模拟研究[J].辽宁工程技术大学学报,2004,23(1):35-37.

[4] 吴智敏,赵国藩,宋玉普,等.光弹贴片法研究砼在疲劳荷载作用下裂缝扩展过程[J].实验力学,2000,15(3):286-292.

[5] 吴智敏,徐世火良,刘佳毅,等.光弹贴片法研究混凝土裂纹扩展过程及双K断裂参数的尺寸效应[J].水利学报,2001,32(4):34-39.

[6] CHANG C W,LIEN H S.Expansion stress analysis of ferroconcrete corrosion by digital reflection photoelasticity[J].NDT and E International,2007,40(1):309-314.

[7] 易成,王长军,刘晋艳,等.两体接触面剪切力学行为的三维数值模拟[J].岩土力学,2008,29(8):2149-2156.

[8] 王长军,杨远志,李勇会,等.接触面力学性能研究及数值分析[J].水利与建筑工程学报,2008,6(4):74-76.

[9] 易成,刘晋艳,王长军,等.两介质接触处光弹性贴片实验及数值模拟研究[J].中国矿业大学学报,2008,37(4):450-455.

[10] 易 成,张亮,陈忠辉,等.轴向受压两体力学模型相互作用的试验研究[J].岩土力学,2006,27(4):571-576.

[11] 王金安,谢和平.剪切过程中岩石节理粗糙度分形演化及力学特征[J].岩土工程学报,1997,19(4):2-9.

[12] 严承蔼.光弹性贴片技术及工程应用[M].北京:国防工业出版社,2003:76-78.