大型滚齿机工作台静压导轨的*压力油流场数值模拟

刘志丹,王时龙,李 川,罗恕燕

(重庆大学机械传动国家重点实验室,重庆 400044)

随着精密齿轮传动的发展,对加工精度可达到 10-7m甚至更高的亚微米、纳米滚齿机的需求与日俱增,而大型数控滚齿机设计制造的关键技术之一的就是工作台支承静压导轨,其性能直接影响到整个机床运行的可靠性,寿命和经济指标。相应地,随着对流体动力润滑导轨的研究日益向广度和深度方向发展,学者们发现静压导轨油膜流场对导轨性能有很大影响[1],但对于油膜压力场、流场分布等问题尚缺乏系统分析,制约了静压导轨的合理设计与应用[2]。

本研究运用流体动力学和摩擦学的相关知识对静压导轨的压力油膜有限元模型进行计算,对某大型数控滚齿机工作台静压导轨油膜的压力场及流场进行了研究,分析了油腔各处的压力、液流流动状况及其对某大型数控滚齿机承载能力的影响,揭示了静压导轨内部的流动规律。

1 静压导轨数值模拟的数学模型

1.1 工作原理

工作台液体静压导轨依靠外部供油系统供给具有一定流量的压力油,建立压力油膜以承受外加载荷,并在预定载荷和任意转速下使工作台与静压导轨处于完全液体摩擦状态,其工作原理如图 1所示。利用专门的供油装置将具有一定压力的润滑油送到导轨的静压油腔内,形成具有压力的润滑油层,利用静压腔之间的压力差形成静压导轨的承载力而将工作台浮升并承受外载荷[3]。润滑油由油泵沿进油孔进入油腔,并沿径向浅腔和外环封油边流出。

图1 定量供油静压导轨工作原理示意图

1.2 基本假设及计算条件

1)静压导轨内部流场中,流体看成不可压缩流体且流态为三位定常流动;

2)润滑油与固体之间无相对滑动;

3)润滑油的惯性力忽略不计且油膜边界压力为零;

4)旋转过程中,不考虑工作台及底座的热变形。

1.3 数学模型

由于静压导轨内部流体随着工作台做旋转运动,因此采用相对参考坐标系来求解。将静止的直角坐标系转换成以角速度 ω旋转的相对参考坐标系,在参考系下,旋转的液体及其边界处于相对静止状态,转速为零。针对稳态流动,采用相对速度,在转动参考坐标系中列出质量守恒方程[4]、动量守恒方程。

质量守恒方程为

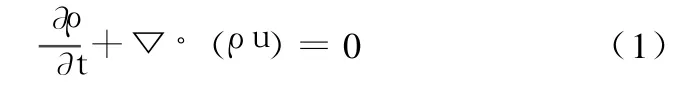
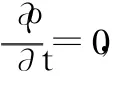
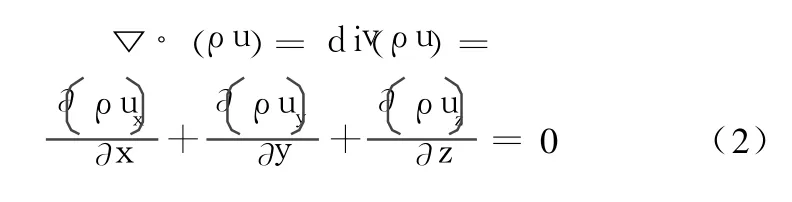
式中:ux,uy,uz分别为速度矢量 u在 x,y,z方向的分量值。动量守恒方程为[5]

式(3)均可展开为 x,y,z三个方向的等式,式(3)中 F表示体力,而静压导轨在旋转过程中只考虑 z方向上的垂直力 Fz,因此 Fx=Fy=0,设置流体物理属性时密度取 900 kg/m3。选择计算流体力学分析软件为求解器,建立求解模型时,选择非耦合求解法的隐式算法,其他默认即可。以上设置完成后,设置边界条件,最后利用初始化流场进行迭代求解。

2 网格划分及边界条件

2.1 网格划分

因静压导轨几何形状复杂,所以采用适用性强,且对具有复杂边界模型特别有效的非结构化混合网格。静压导轨三维几何实体模型是在专业三维CAD软件下生成的,再调计算流体力学分析软件前处理器进行网格划分。静压导轨底座和流体图形见图2和图 3。

图 2 静压导轨底座

图 3 流体图形

在计算求解区域内的流态分布时,流体所在区域的网格数量直接影响计算结果。文中经多次试算,找到了计算结果基本不随网格数变化的情形,流体网格总数为246 562,工台网格总数为331 525,底座网格总数为302 673。

2.2 边界条件设置

2.2.1 边界条件计算

某大型滚齿机工作台静压导轨的油腔结构如图 4所示,令工作台直径为D,工作台自重 G,工件最大质量 W,采用恒流开式静压导轨结构,计算六垫静压圆导轨副的性能。结构尺寸如图 4(a)所示。

对于圆导轨,由于其直径相对于油腔的径向宽度是很大的,油腔数目又比较多,所以计算油垫的有效承载面积时可把扇形油垫简化为矩形油垫,如图 4(b)所示。

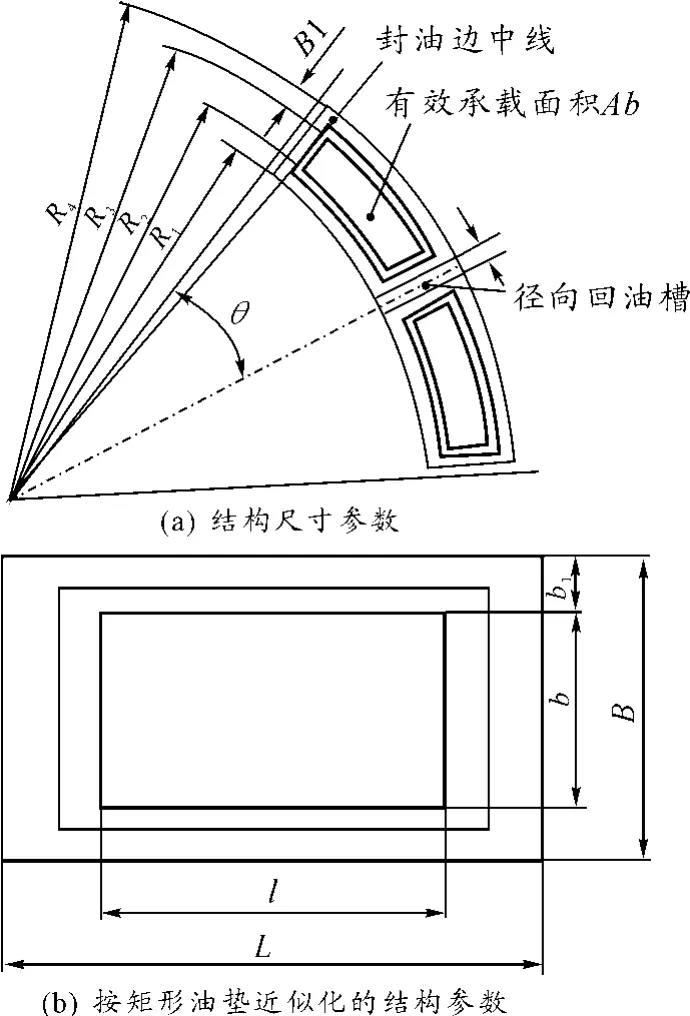
图 4 静压导轨油腔结构

根据导轨结构可初步确定导轨外径R4、内径 R1。径向封油边的宽度b1可按 b1=(R4-R1)/4选择合适值。根据径向封油边宽度计算导轨油腔内径R2,R3为

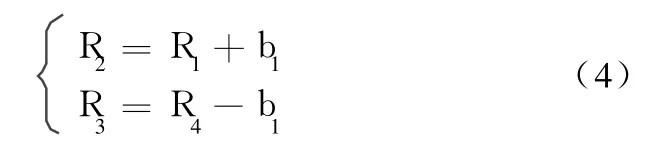
因为静压导轨为多油腔,每个油腔除外环回油外,还设置径向回油槽,径向回油槽作用有两个:既可作内回油道,还可作油腔之间断压槽用,以免压力互相干扰[6]。

一般取径向封油边与周向封油边相等,根据初选的导轨参数,由图 4计算导轨油垫尺寸:

式中 l1为径向回油槽宽。

每个油垫的油腔压力

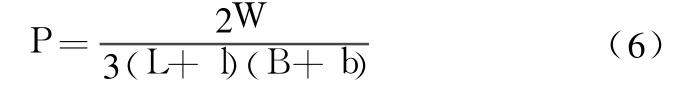
式中 W为最大载荷(工作台自重 G+工件重量 W)。

计算每个油垫的流量为

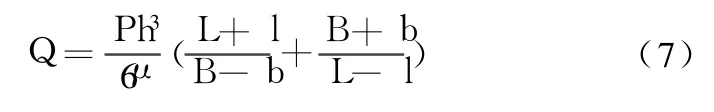
式中:μ为机械润滑油的动力黏度;h为在载荷为W时的油膜厚度。

某大型数控滚齿机实际工作参数为:工作台直径为1 460mm,最大工件直径 d=1 600mm,工作台自重G=2.92 t,工件最大重量 W=7 t,工作台采用图 1所示原理的恒流开式静压导轨结构,其中导轨内径R1=635mm,外径R4=705mm,径向回油槽宽 l1=10mm,机械润滑油的动力黏度 μ为0.028 8 Pa◦s,最小油膜厚度 h为0.06mm。把实际工作参数代入理论公式(4)-(7)中,得到每个油腔的进油压力为 0.467MPa,流量为 2.375×10-5m3/s。经计算得Re小于2 300,导轨内部为层流状态,因此采用Lam inar模型对静压导轨内部流场进行求解。

2.2.2 设置边界条件

对底座及工作台的两侧面做周期性边界条件设置,这样可保证只研究静压导轨的1/6个油腔即可反映所有油腔的流态。由流量和进油管道形状计算出进口处速度 v=0.473m/s,压力在进口截面上设为均匀分布。进口高度L=100mm,直径 D=8mm,出口处选取压力出口边界条件,而回油槽处压力为大气压。固壁上速度满足无滑移条件,建立与轴线重合的直角坐标系(x,y,z),将直角坐标系(x,y,z)固定在中心轴上。

3 数值计算结果及分析

在旋转流动过程中,方程采用有限体积法求解,方程求解控制参数相对误差为 1×10-6,其他均为 1×10-3,压力、速度的欠松弛因子均为 0.3,其他为 1。在上述条件下,方程组采用分离、隐式求解获得收敛。

经过以上步骤的分析及计算,首先得到迭代计算后的残差曲线和油膜的压力场和流场分布图。其中图5为油腔的残差曲线,图 6为油膜绝对压力,图 7为流线速度矢量。

图 5 油腔迭代残差曲线

图 6 油膜绝对压力

图 7 流线速度矢量

图 6反应了工作中静压导轨的压力分布情况,从图中可以大致看出高压区和低压区位置,从图中可以看出进油口处压力最大,静压导轨的承载面的压力符合理论计算结果,压力分布比较均匀,而因为油液从回游槽处流出,因此压力最小。由图 7可以看出,速度在半径方向由里向导轨外周逐渐增大,直到外边缘达到最大,验证了实际上流体的线速度与导轨半径成正比分布的结论,而静压导轨的油腔分界部位结构有突变,因此出现速度最大的状况,为了避免出现速度过大的情况,建议改进油腔分界部分的机械结构,如对此部位采用增加倒角等改进方法。由于静压导轨本体质量和回转半径大等特点,要求工作中回转速度不能太高,在转速不高的情况下油腔深处(如静压导轨回游槽处)流体速度较低,有可能出现回流现象且回油槽边缘处出现低速区,容易发生气蚀现象,这一结果与实际基本吻合。以上云图中数值与左侧颜色带对应,具体数值可在流体仿真软件信息窗口获得。

4 结束语

本文中利用CFD技术对液体静压导轨进行三维数值模拟,建立了大型数控滚齿机静压导轨的压力油膜模型,并对静态下的油膜压力场与流场进行迭代数值计算,得到包括压力分布及流场分布情况,计算结果能够有效反映导轨内的流动状态,解决了实际工程中由于油膜很薄导致大型数控滚齿机的静压导轨内部压力场分布无法通过直接测量获得的问题,揭示了导轨内部流动的特殊规律和流动机理,弥补了试验方法没有理论依据的不足。采用这种方法可提前预测大尺寸静压导轨润滑的特性,这对提高静压导轨的工作效率以及降低经济损失有一定的促进作用。在静压导轨的三维设计及整个流场分析过程中,完成了不相关软件之间的相互连接,取长补短,实现静压导轨油膜态的数值模拟。

综上所述,将流体仿真技术应用于液体静压导轨的优化设计当中,对提高静压导轨的各项性能将起到一定的参考价值。

[1] 卢华阳,孙首群.液体静压导轨支承油膜的有限元分析[J].机床与液压,2007,35(10):46-49.

[2] 王勇勤,王荆,江桂云,等.高精度动静压油膜轴承设计方法研究[J].重庆工学院学报,2006,20(5):5-8.

[3] 陈燕生.静压支承原理和设计[M].北京:国防工业出版社,1980.

[4] 马希直.滑动轴承瞬态热弹性流体动力润滑性能分析及实验研究[D].西安:西安交通大学,2002.

[5] 王福军.计算流体力学分析-CFD软件原理与应用[M].北京:清华大学出版社,2004.

[6] 杨沛然.流体润滑数值分析[M].北京:国防工业出版社,1998.

(责任编辑周江川)