不同故障状态的 MTBF计算及应用

付永涛,章文晋

(北京航空航天大学可靠性与系统工程学院,北京 100191)

MTBF是评价系统可靠性性能的一个重要指标。在GJB451A—2005中,MTBF[1]是指可修复产品的一种基本可靠性参数,其度量方法为在规定的条件和规定的期间内,产品寿命单位总数与故障产品总数之比。这里的产品故障通常是泛指系统的所有故障。而系统发生的故障往往是不一样的,经常会处于不同的故障状态,不同故障状态对系统的影响通常是不一样的。例如对机载计算机来说,故障可能是由于大容量存储设备导致航电系统不能读取地图等数据,或是由于通用处理器导致航电系统无法进行数据处理,这 2种故障状态对系统造成的影响是不一样的,通用处理器的故障对航电系统的影响更为恶劣。在工程上,知道某一类对系统产生严重影响的故障状态的 MTBF,可以针对性地提高系统的可靠性和开展维修保障工作。因此计算不同故障状态的 MTBF对于提高系统不同部件的可靠性和安全性有着重要的参考意义。目前,国外学者对于不同故障状态的 MTBF计算方法已经作了一些研究,并得出了不少成果[2-4],但其中一些计算方法过于繁琐,为此本文提出了一种相对易于计算的方法。

1 不同故障状态的 MTBF计算方法

1.1 传统计算不同故障状态MTBF方法的缺陷

传统计算 MTBF的计算方法是利用MTBF的定义,即产品故障时间这一随机变量的期望值来计算的。这样从数学上可以对产品故障密度函数求期望值来计算。对于不同故障状态的 MTBF计算,传统的计算方法可以通过以下例子来说明。

假定某一系统的故障状态主要分为2种:分别为F1和F2;其故障率分别为 λ1,λ2;系统服从指数分布,系统发生故障之后进行的修复是完全修复。下面分别计算发生这 2种故障状态的 MTBF及系统的 MTBF。

在计算之前,先介绍一下马尔可夫过程。系统不同状态的转移都只仅与前一时刻的状态有关,而与过去的状态无关,或者说状态转移过程是无后效性的,则这样的状态转移过程就称为马尔可夫过程。在区域开发活动中,许多事件发展过程中的状态转移都是具有无后效性的,对于这些事件的发展过程,都可以用马尔可夫过程来描述。

该系统的马尔可夫状态转移图如图1所示。其中状态W为初始系统工作状态,F1,F2分别为系统的 2种故障状态,状态 W向 2种故障状态转移的转移率为 λ1和 λ2。

图 1 系统马尔可夫模型

由马尔可夫理论可知,该系统的转移密度矩阵为

从计算结果中可以看出F1,F2故障的MTBF值小于系统的 MTBF值,而这与工程常识相悖,F1,F2的 MTBF应大于系统的 MTBF。上面的计算方法是严格按照 MTBF的定义计算的,之所以会出现这种问题是因为计算 MTBFF2时,计算的期望值可以分为 2部分:

1.2 不同故障状态的MTBF计算方法

传统的计算方法无法求出系统某一故障状态的 MTBF,本文提出一种新的思路来计算。

故障状态F2的MTBF是指系统从正常工作开始到系统发生 F2故障时间的平均值,在此期间内无论发生几次F1故障,都对 F2的 MTBF值无影响。因此,在计算 F2故障的 MTBF中应不考虑 F1的故障次数,即在发生故障 F2之前不应考虑系统处于状态F1的时间。

这样在计算 F2的MTBF时,可以将 F1作为吸收状态,每次发生 F1故障之后,系统进行完全修复。系统由状态F1向系统工作状态 W转移。即故障 F1发生之后,有修复率 μ向状态 W转移。计算 F2的MTBF时,由于不考虑系统处于状态 F1的时间,可以将 F1的平均修复时间(MTTR)设为 0,即假定修复率 μ趋于无穷。

此时系统的马尔可夫状态转移图可以转换为如图 2所示。

图 2 系统更改后的马尔可夫模型

系统的状态转移概率矩阵变为

此时系统的 MTBF即为 F2的 MTBF。利用 MTBF的矩阵计算方法[5]可以求得系统的 MTBF。先将矩阵P去掉吸收状态的行和列,得一截阵

用单位矩阵 I减去Q,并对 I-Q求逆矩阵得

该逆矩阵的第 1行之和,即为系统的 MTBF,也即 F2的 MTBF。此时 MTBFF2为

处于状态 F1的时间对 F2的 MTBF值应无影响,因此可假定修复率 μ趋于无穷,所以 F2的 MTBF应为

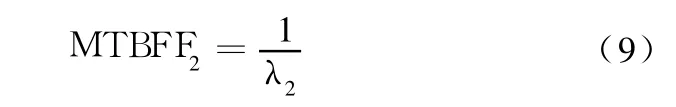
以上方法是针对 2种故障状态的系统,对于多种故障状态的MTBF计算方法类似。只需将不必计算的故障状态的MTBF其马尔可夫状态改为吸收状态,并将其修复率假定为无穷。更改后的马尔可夫模型的系统的MTBF即为所要计算的故障状态的 MTBF。

在安全性领域,系统在发生故障以后,按系统所处的状态可以将故障分为安全性故障和危险性故障。安全性故障是系统在发生该类故障以后,不会造成人员伤亡、职业病、设备损坏、财产损失或环境损害的故障;危险性故障是指系统在发生故障以后,会造成人员伤亡、职业病、设备损坏、财产损失或环境损害其中一方面的故障。系统的状态逻辑如图 3所示。因此系统的MTBF可以分为 2种:平均危险故障间隔时间(MTBFD)和平均安全故障间隔时间(MTBFS)[6]。与此对应的是两种故障状态的故障率 λd和λs。MTBFD和 MTBFS可以为系统安全性定量评价提供参考意义。

图 3 系统状态逻辑

2 常见容错系统的 MTBFD计算

目前,工业上安全关键控制系统多采用冗余的方法来提高系统的可靠性、增强系统的容错能力。常用的冗余方法包括硬件冗余、软件冗余、信息冗余、时间冗余等。虽然冗余方法提高了系统的成本,但也大大提高了系统的可靠性。下面以常见的容错控制系统为例来计算相应的MTBFD。

2.1 2oo2D结构的MTBFD计算

2oo2D结构是控制系统常用的容错结构。其结构组成是由 2个执行相同功能单元并联组成,其输出共同组成系统的输出,当检测模块检测到单元故障时,会自动隔离故障模块;系统输出由正常工作的模块决定。其结构模型如图 4所示。

图 4 2oo2D结构

现以 2个相同单元并联的 2oo2D结构为例,假定功能单元发生危险故障的故障率为λ,每个单元自检测模块的故障诊断覆盖率为 Cd,故障诊断覆盖率是指被检测到的故障总数占系统中所有可能的故障总数的比例。当系统发生故障且自检测模块都检测到故障的发生时,系统处于故障-安全状态。当 2个模块都发生故障时且模块至少有 1个未检测到故障的发生时,系统处于故障 -危险状态。系统的马尔可夫状态转移图如图5所示。

图 5 2oo2D结构的马尔可夫模型

从安全性的角度考虑,工程上更关心的是 MTBFD的数值,因此在此只计算 MTBFD的值。为计算系统的 MTBFD,需要将 FS状态由吸收状态变为瞬时状态,由于修复率μ趋于无穷,进而可以将状态FS取消。其中马尔可夫模型转换如图 6所示。

图 6 转换后的 2oo2D结构的马尔可夫模型

转换后的 2oo2D结构的马尔可夫状态转移矩阵为

去掉吸收状态的行和列,并用单位矩阵减去该截阵得矩阵:

系统的 MTBF即为 I-Q的逆矩阵第 1行之和。经计算可知该 2oo2D结构的MTBFD为

从中可以看出为提高系统的 MTBFD值,除了要降低故障率之外,提高故障诊断覆盖率也是提高 MTBFD的一种重要措施。

2.2 三模冗余系统(TMR)MTBFD计算

TMR是控制系统中典型的容错结构。其结构组成是由 3个相同的模块并联工作,当系统有 2个或 2个以上单元工作时,系统能正常工作,系统决策是由一表决器进行的。其结构模型如图 7所示。

图 7 TMR结构模型

为进一步提高TMR结构的安全性,每个功能单元都配置故障检测单元。当故障检测单元能检测到故障的发生时,系统不会发生危险性故障。在计算该系统的 MTBFD之前,先定义系统的 2种状态——故障 -危险状态和故障-安全状态。当故障发生时检测模块没有检测到故障的发生且表决模块故障时,系统处于故障 -危险状态;而当 2个或 2个以上故障发生时能检测到故障的发生或表决器未发生故障时,系统处于故障-安全状态。

假定每个故障检测单元的故障诊断覆盖率为Cd,表决器可靠度为 R,功能单元发生危险故障的故障率为λ。系统的马尔可夫状态转移过程如图 8所示。

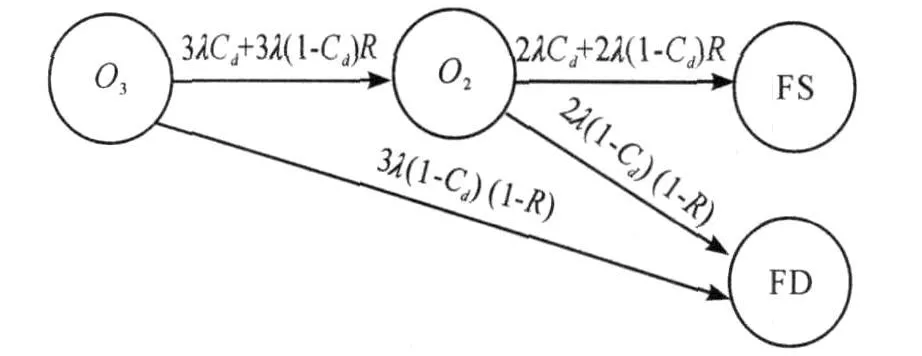
图 8 TMR的马尔可夫模型

在计算系统的 MTBFD时,应不考虑状态FS的影响,所以状态 FS可以向 O2和 O3状态转换,设分别有修复率μ1和 μ2。μ1和 μ2可以假定趋于无穷,进一步可以将状态FS取消,其马尔可夫转换过程如图 9所示。

图 9 转换之后的TMR的马尔可夫模型

计算该变换后系统的 MTBF就是原系统的 MTBFD。变换后的马尔科夫状态转移矩阵为

从中可以看出系统的 MTBFD不仅与故障率成反比,还与故障诊断覆盖率成正比。所以要提高系统的MTBFD,一方面要提高系统的可靠性,另一方面还要提高系统的故障诊断能力。

3 应用

西门子公司产品在过程工业,机械制造工业,医药工业、石化工业等多个领域的自动控制中得到广泛应用,并将这些领域的安全保护作为一个重要的方面。这里以西门子在机床安全保护系统中的某型分布式安全装置为例,介绍MTBFD的应用。

西门子的分布式安全装置控制系统采用 2oo2D控制结构。已知其中功能单元的危险故障率 λ=2.5×10-7h,故障诊断覆盖率为 Cd=0.95。根据前面的计算公式(12),将数值代入公式可得该系统的 MTBFD为

从计算结果中可以得出,该控制系统发生一次危险性故障的期望时间是 220万h。从数值上看,系统的安全性能可以接受。

4 结束语

MTBF作为评价系统可靠性的一个重要指标,通常是把所有故障状态都算进系统的MTBF值中。在工程上,知道某些对系统影响比较严重的故障状态的 MTBF值,往往更具有实际意义。而目前国内在理论上对于不同故障状态的MTBF计算方法不多。本文提出了一种计算不同故障状态的MTBF方法,对于计算系统的MTBFD和 MTBFS具有一定的参考意义,进而为系统的安全性能定量评价提供参考。

[1] GJB 451A—2005,可靠性维修性保障性术语[S].

[2] Toon Choi,Kishor S.Trivedi.Conditional MTTF and its Computation in Markov Reliablity Models[C]//PROCEEDINGS Annual RELIABILITY AND MAITAINABILITY Symposium.[S.l.]:[s.n.],1993,56-63.

[3] Todd A.Delong,D.Todd Smith.Dependability Metrics to Assess Safety-Critical Systems[J].IEEE TRANSACTIONSON RELIABILITY,2005,54(3):498-505.

[4] Julia V.Bukowski,William M.Gob le.Defining Mean Time-to-Failure in a Particular Failure-State for Multi-Failure-State Systems[J].IEE TRANSACTIONS ON RELIABILITY,2001,50(2):221-227.

[5] William M.Goble.控制系统的安全评估与可靠性[M].白焰,译.北京:中国电力出版社,2008.

[6] 刘建侯.功能安全技术基础[M].北京:机械工业出版社,2008.

(责任编辑陈 松)