基于EDA技术的电路容差分析在电路设计中的应用

李慧贞， 李春霞

(陕西科技大学电气与信息工程学院， 陕西 西安 710021)

0 引言

实际电路中元器件参数和其标称值之间是存在着随机误差的，例如，一个标称值为47 kΩ，容差是10%的电阻，其阻值可以是42.3 kΩ到51.7 kΩ范围内的任何值.在电路设计中，往往都是从标称值开始设计的，故这种标称值下设计的电路和实际电路产品之间存在着一定的性能差别，且随使用时间增长及环境温度的改变还会使这种差别增大，最差的情况下，这种偏差可能会影响产品的正常使用，造成产品功能失效；另外，元器件容差和其成本直接相关.容差范围小，精度高，价格高，故在设计电子产品时只有充分考虑容差因素，才能设计出可靠性好、性价比高的电子产品.

1 电路容差分析及其EDA实现

电路容差分析是在给定电路元器件参数容差范围的条件下，计算元器件参数变化对电路性能的影响.通过容差分析，我们可以发现元器件参数容差对电路性能影响的大小，从而优化我们的设计，将电路性能偏差控制在允许的范围内.对电路进行容差分析有两类方法，一类是以灵敏度分析为基础进行，单独的灵敏度分析只是解决单个元器件参数变化对电路性能的影响，而容差分析则利用多个灵敏度信息解决多个元器件参数偏离标称值时对电路性能的总影响，即最坏情况分析(Worst Case Analysis)；另一类是以概率统计方法为基础，通过已知元器件参数的随机分布规律计算电路特性的分布规律，蒙特卡罗分析(Monte Carlo Analysis)就是这种抽样统计的方法，该方法在器件参数容差范围内对参数进行随机抽样，对大量的抽样值做电路仿真，计算出电路性能的统计特性和偏差范围.

EDA(Electronic Design Automation)技术为大型、复杂电路分析提供了方便，同时也使计算机辅助电路分析成为可能.计算机辅助电路容差分析弥补了传统容差分析方法随机模拟困难、计算量大、参数调整缺乏灵活性的缺陷，使得对大规模电路进行容差分析与设计成为可能.该分析是建立在电路拓扑结构及元器件模型基础上实现的，故其结果更接近于真实的电路测试结果. OrCAD/Pspice 提供了蒙特卡罗和最坏情况分析来分析电路中元器件参数数值变化对电路性能的影响，本文以滤波器电路为例说明了在OrCAD/Pspice下进行电路容差分析的方法，并对其结果进行了讨论.

2 蒙特卡罗法的OrCAD/Pspice实现

蒙特卡罗分析是随机抽样、统计分析的方法，该方法采用随机数发生器按生产时所用元件值的实际概率分布来选择元件，从而可在元器件模型参数赋予的容差范围和分布规律内进行各种复杂的分析，包括直流分析、交流及瞬态特性分析，由分析结果可估算电路性能的统计分布规律及统计参数，据此对电路批量生产时的成品率及成本等做出预测，它模拟了电子电路的实际生产情况.下面通过一个Chebyshev 4阶有源滤波器电路说明该方法.图1滤波器是按中心频率为10 kHz，带宽为1.5 kHz设计，现应用OrCAD/Pspice中的蒙特卡罗分析预测大批量生产时由于RC元器件参数偏差引起中心频率发生偏差的情况，再结合一定的约束条件判断出实际生产时该采用多高精度的元件.假设投入生产时要组装100套滤波器，所有电阻采用精度为1%的电阻器，所有电容采用精度为5%的电容器，且设元器件参数分布服从正态分布(高斯分布)，在蒙特卡罗分析中设置分析次数为100次，环境温度为+27 ℃.

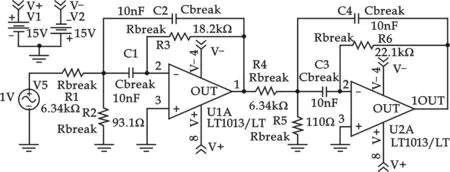
图1 Chebyshev 4阶有源滤波电路

图2所示的统计直方图是在交流分析后启动电路性能分析(Performance Analysis)得到的，据此分析电路特性随元器件参数容差变化的关系，目标函数选(CenterFreq(V(out),1)，其表示滤波器频响曲线从最大值下降1 dB时滤波器带宽的中心频率.

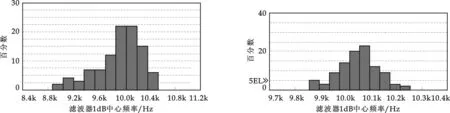
图2 电阻容差为1%、电容容差为5%时滤波器 图3 电容、电阻容差都为1%时滤波器 1 dB带宽中心频率直方图 1 dB带宽中心频率直方图

该直方图的水平坐标轴对应了目标函数的取值，即滤波器1 dB带宽中心频率的随机分布值，柱状图的高度表示落入相应频率范围内样品的个数占总样品数的百分比.该直方图的实际意义相当于用一批容差为1%、5%，分布类型为正态分布的RC元件试投产了100个产品，分别测出每个滤波器中心频率的实际值，然后将所测频率的最低值与最高值区间分为10个相等的间隔，对滤波器中心频率值落在每个间隔中的产品数量进行统计，由统计结果做出直方分布图.可以看出，该直方图是呈正态分布的.

直方图分析还同时给出了统计分析的结果，如直方图样本数nsamples=100，直方图X坐标数据范围划分区间(ndivision)=10，样本的平均值(mean)=9 916.98，标准偏差(sigma)=355.917，样本最小值(minimum)=8 871.53，样本最大值(maximum)=10 536.2，中位数(median)=10 014.1，10%分位数(10 th%ile)=9 448.57，90%分位数(90 th%ile)=10 326.8.其中“中位数”就是50%分位数，即将整个样本从小到大排列正好处于中间位置的那个样本.如果样本总数为奇数(即2n+1个)，则50%分位数就是第n+1个样本的大小；如果样本总数为偶数(即2n个)，则50%分位数就是第n个样本和第n+1个样本的平均值.同理，“10%分位数”对100个样本来说是第10号样本和第l1号样本的平均值，90%分位数是第90号样本和第91号样本的平均值.

表1 正态随机变量取值与中心值偏离kσ时的出现概率

从统计数据可见滤波器中心频率的中心值(Median)等于10 014.1 Hz，与设计要求非常接近，Sigma为355.917,为中心频率的标准偏差σ.由概率论知识可知，正态随机变量X位于中心值附近的密集程度可由标准差σ来度量.正态随机变量取值偏离中心值不超过一个σ的出现概率为68%，不超过Kσ的出现概率如表1所示，从表1中看到偏离均值为3σ以外的概率相当小，只有0.3%.

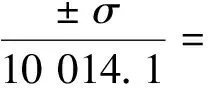
3 最坏情况分析的OrCAD/Pspice实现

由于灵敏度不同，当电路中不同元器件分别发生变化，即使元器件值的变化幅度相同，但引起电路特性变化的绝对值会不同，且其变化的方向也可能不同.当电路中多个元器件同时随机变化时，它们对电路特性的影响会相互起“抵消”的作用.进行最坏情况分析时，是按引起电路特性向同一方向变化的要求，分别确定每个元器件的(增、减)变化方向，然后再使这些元器件同时在相应方向按其可能的最大范围变化，对电路特性来说，这就是一种最坏情况.在这种情况下进行的电路分析就叫作最坏情况分析(Worst Case Analysis)，简称WC分析.图4为由集成运放构成的有源高通滤波器，其截至频率为54 kHz，现用最坏情况分析它的频率响应.

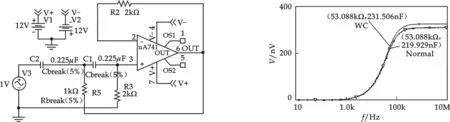
图4 由集成运放构成的高通滤波器 图5 最坏情况分析结果

整理函数选为YMAX，此时最坏情况被定义为使高通滤波器的频响在元器件容差范围内变化与标称值的频响幅度差为最大，并且使输出向增至最大的方向变化，即最坏情况以输出V(out)的幅频特性曲线上最大值“变大”为最坏方向.所以，图5中的最坏情况下频响曲线上的幅值总是大于标称值时的频响曲线上的幅值.打开*.out文件可以查阅到整理函数筛选出的总结数据：

SORTED DEVIATIONS OF V(out) TEMPERATURE =27.000 DEG C

WORST CASE SUMMARY

RUN MAX DEVIATION FROM NOMINAL

ALL DEVICES 16.3640E-09 higher at F =9.7746E+06

(105.26% of Nominal)

该数据表明在频率为9.7746E+06 Hz时，电路的频响值与标称值下的频响值偏差达到最大，即最坏情况，是标称值情况下的105.26%.图5中，WC曲线是最坏情况时高通滤波器的频响曲线，Normal曲线是元器件参数为标称值的情况下高通滤波器的频响曲线.由图5可看出，在最坏情况下滤波器的截止频率发生了偏移.值得注意的是只有电路特性在所有参数的容差范围之内相对于每个参数的变化都是单调时，最坏情况分析计算出的结果才是正确的，否则将导致错误的结果[1].最坏情况分析不同于蒙特卡罗分析，它得到的是所有容差元件引起的电路性能指标的最大偏差，最大限度地决定了元件所能容许的误差.虽然实际生产中，这种情况出现的概率很小，是一种很保守的情况分析，但它对衡量产品的质量是非常重要的，即通过了最坏情况分析的设计其可靠性也是最好的，虽然对大批量生产的电子产品不一定是最经济有效的设计方案，因其对元器件质量要求可能过高，但对于航天、反应堆等一些风险较大的设备中的电路，通常要求零失效率，其成本往往不是第一位的考虑因素，故往往考虑最坏情况指导下的电路设计方案.

4 结束语

应用EDA软件OrCAD/PSpice所提供的容差分析，即蒙特卡罗和最坏情况分析，在电子电路产品大批量投产前，按照元器件参数值的容差统计分布规律，模拟实际电路生产中元器件参数容差变化对电路性能的影响，可以为实际生产提供有意义的依据，如器件容差的确定、产品的成品率预测、性价比预测等，还可预见产品是否具有较好的可靠性，从而节省设计时间和降低设计费用，提高电子产品的设计效率，该方法最大的优点是用最低的元器件代价得到满足设计指标要求的电路特性.

[1] 杨华中. 电子电路的计算机辅助分析与设计方法[M].北京：清华大学出版社, 2008.

[2] 李慧贞. 基于PSpice的电路灵敏度分析及其在电路设计中的应用[J] .陕西科技大学学报, 2005,(3):70-72.

[3] 贾新章.电子电路CAD技术——基于OrCAD9.2[M].西安：西安电子科技大学出版社,2002.

[4] 胡怡红.林莘信号处理[M].北京：人民邮电出版社,1999.

[5] 李宏伟. 容差分析仿真方法在某航空产品电路设计中的应用[J]. 航空兵器，2005,(6):43-46.

[6] 刘春志, 杜 鑫, 曾晨晖.电路功能可靠性仿真分析技术[J]. 航天器环境工程， 2009,(6):272-276.