INFLUENCE OF ROTATION ON A CELL IN NEUTRON STAR OUTER CRUST
2010-02-25LIBaojiangLISinongCHENWei
LI Bao-jiang, LI Si-nong, CHEN Wei
(Department of Physics, Jinan University, Guangzhou 510632, China)
0 Introduction
A star which is composed of neutrons, that is the neutron star, was predicted by Landau after Chadwick found the neutron in 1932[1]. According to the present theory, a neutron star is one of the possible ends of a star. It is born in the aftermath of a successful supernova explosion as the stellar remnant with massive stars(4M⊙≤M≤8M⊙) used up the nuclear fuel. The discovery of the Crab and the rapidly rotating pulsar (PSR0531) in its remnant as well as SN1987A supports this theory. The later observations make the neutron star′s image in people′s mind fullness continuously: the first theoretical calculation of neutron stars was performed independently by Tolman[2], Oppenheimer and Volko[3]in 1939 and Wheeler around 1960; the first neutron star as a radio pulsar was discovered by Bell and Hewish in 1967[4], and was identified as a rotating neutron star by Pacini[5]; the Pulsar is a neutron star in the high speed were identified by Gold in 1968; the first binary pulsar was discovered by Hulse and Taylor in 1973.
Neutron stars have been absorbing many author′s attention due to their extreme condition such as high density, strong magnetic field etc. And they are usually regarded as the natural laboratory for the research of nuclear and particle physics. Up to now, the neutron stars have been studied extensively and deeply. First, the mechanism for the birth of neutron star and its evolution was discussed in detail[6]. Second, the mass of neutron star is found to be about 1.4 MJ and its radius to be 10 km[7]. In further, the rotating and gravitational property of these stars were also studied[8].
In these works, the equation of state (EOS) of neutron star matter is a key input. There are various factors which influence the EOS of neutron stars. The composition of neutron star matter is an important factor which decides its EOS. The composition of neutron star matter is different in different region of a neutron star. In the surface region of neutron stars, with typical densityρ< 106g/cm3, there exist iron atoms. In the outer crust, the density about 106g/cm3<ρ< 4.1011g/cm3is a solid region where a coulomb lattice of heavy nuclei coexist inβ-equilibrium with a relativistic degenerate electron gas. In the inner crust, the density about 4.1011g/cm3<ρ< 2.1014g/cm3consists of a lattice of neutron-rich nuclei together with a superfluid neutron gas and an electron gas. We usually study the EOS of neutron star matter in these two regions by the concept of cell which appears in solid physics[9]. The neutron liquid for 2.1014g/cm3<ρ< 1.1015g/cm3contains mainly superfluid neutron with a smaller concentration of superconducting protons and normal electrons[10]. At higher densities, there may be hyperons and quarks, and many phase transition such as pion or kaon condensation etc. may take place. The neutron star matters in these regions are usually regarded as uniform nuclear matter inβ-equilibrium and charge neutrality when we study its EOS.
The temperature, magnetic field etc. are also the factors that cannot be neglected. On the other hand, neutron stars rotate rapidly, and the speed in the surface access to the speed of light. The relativistic effect on the cells in the surface of neutron star should be significant since these cells move with the neutron star. The influences of translating and rotating on the EOS of nuclear matter had been studied by some authors, then these influences on the EOS of neutron star matter are an interesting subject. We study the energy density, neutron density and scalar density of the cell in different speed of rotation of neutron star, and the cell is considered to be composed of pure neutron star matter in this paper for simplicity.
1 Theoretical Model
In the first instance, we introduce a model of relativistic quantum field theory for the nuclear many-body system. The Lagrangian density for this model is given by
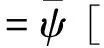
(1)
with
Fμv≡∂μVv-∂vVμ
(2)
ψ,φ,Vμare the field of neutron, scalar meson and vector meson, respectively.gs,gvare the coupling constants between neutron and scalar, vector meson, respectively.c,dare the self-coupling constant of scalar meson, they are decided by the saturation property of infinite symmetric nuclear matter, andM,ms,mvare the mass of neutron, scalar meson and vector meson, respectively.

Lagrange′s equations
(3)
Whereqiis one of the generalized coordinates, yield the field equations

(4)
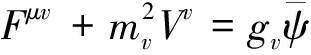
(5)
[γμ(i∂μ-gvVμ)-(M-gsφ)]ψ=0
(6)
Equation (4) is simply the Klein-Gordon equation with a scalar source. Equation (5) looks like massive QED with the conserved baryon current
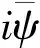
(7)
Finally, Equation (6) is the Dirac equation with the scalar and vector field introduced in a minimal fashion.
The energy-momentum stress tensor is defined by
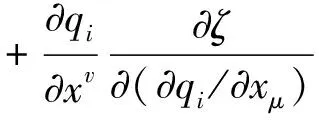
(8)
Where the repeated indexiis summed over all generalized coordinates. The substitution of our previous expression into Eq.(8) and subsequent use of the field Eq.(6) leads to
+∂vφ∂μφ+∂vVλFλμ
(9)
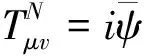
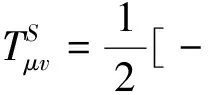
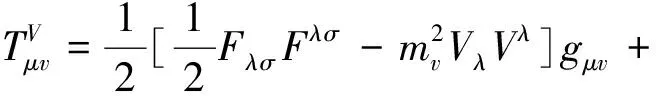
We work in the mean field approximation, namely,φ,andVμare treated as their mean value <φ> and
(10)
(11)
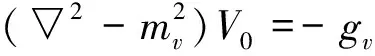
(12)

The angular momentum density is given by
L0μv=T0μxv-T0vxμ
(13)
Where repeated Latin indicates are summed over the space components only,it can be solved:
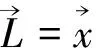
(14)
In the Thomas-Fermi (TF) approximation, we minimize the energy density and incorporate the constrains through Lagrange multipliersμandω:
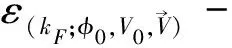
(15)
Here theρBandLare independent of these quantities. At the same time, the stability of nuclear matter needs:
(16)
The fields may be held constant during the variation of the surfaceδkF. The remaining calculation yields an equation for the Fermi surface:
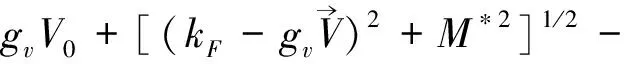
(17)
Where
β≡ω×X
(18)
The effective mass is defined to be
M*=M-gsψ
(19)
In order to make calculation convenient, we introduce the “kinetic momentum”:
(20)
The resulting equations are then given by

(21)
(22)
(23)
The equation for the Fermi surface Eq.(17) becomes
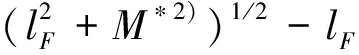
(24)
Where the effective chemical potential
(25)
Given the form of the Fermi surface in Eq.(17) it is possible to do the integrals over wave numbers with no further approximation. It is straightforward to show that:
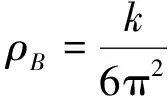
(26)
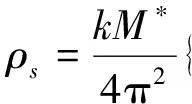
(27)
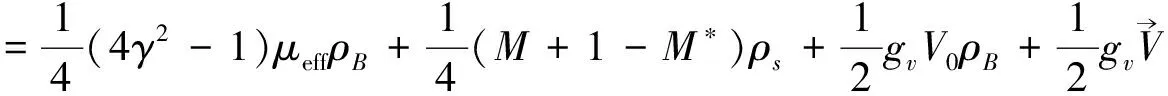
(28)
Where
γ=(1-β2)-1/2
(29)
2 The Numerical Results
The values of parameters we adopt here aregs=8.839,gv=9.78,c=3 415.58,d=-22.06, respectively. They are fitted to reproduce the saturation property of infinite uniform symmetric nuclear matter. Using these parameters we study the energy density, neutron density and scalar density of neutron matter in cylindrically symmetric cell and spherical symmetric cell which are in the surface of a neutron star with radiusR= 12 km. And this neutron star is assumed to rotate with a period of 1.337 s, 0.09 s and 0.5 ms (the period of CP1919[4], Vela and a pulsar in SN1897 remnant), respectively.
In order to simplify the Eq.(11) and Eq.(12), we assume that the field of vector meson keeps invariant everywhere in the cell. And now only Eq.(10) remains to be integrated.
2.1 The cylindrically symmetric cell
In the cylindrically symmetric cell, the Eq.(10) can be reduced to
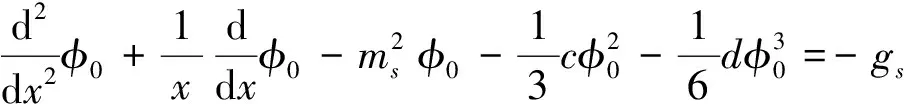
(30)
The boundary condition is:
ρB=0,x≥Rc
(31)

(32)
The energy density and neutron density of neutron matter at different position in the cylindrically symmetric cell are shown in Fig.1 and Fig.2, respectively. The solid, dotted and dashed curves represent the cell is in the surface of a neutron star rotating with the period of 1.337 s, 0.09 s and 0.5 ms, respectively, and the first two coincide with each other. We can see that the rotation may have a significant impact on the property of the cell if the neutron star rotates with the period of 0.05 ms. On the other hand, the energy density and neutron density become zero at r = 5.73 fm.This is almost the maximum radius of the cell we can obtained in our numerical calculation. And these results are consistent with Ref.[9]. Fig.3 represent the scalar density in the same condition with Fig.1 or Fig.2, it can be see that the rotation has no influence on the scalar density.
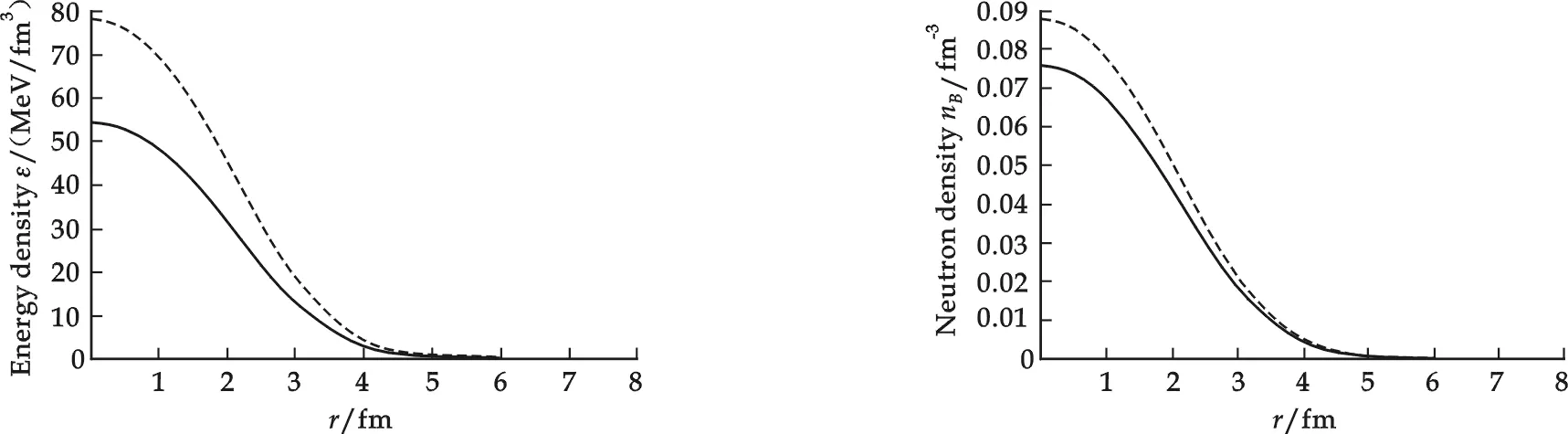
Fig.1The distribution of the energy density of neutron matter in the cylindrically symmetric cell
Fig.2The distribution of neutron density in the cylindrically symmetric cell that the average density is about0.03fm-3
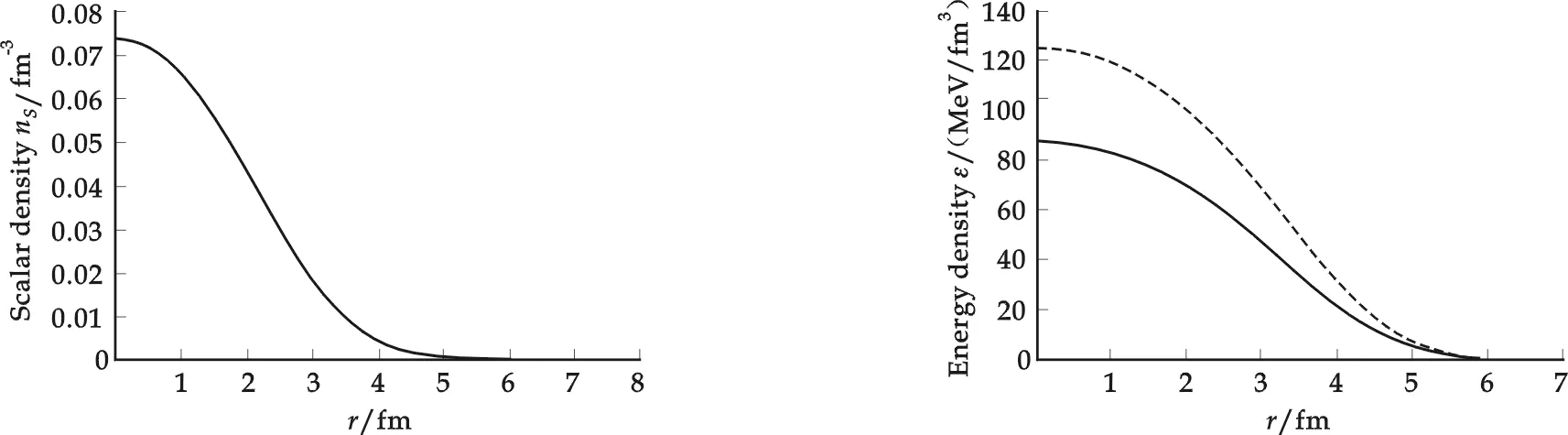
Fig.3The distribution of scalar density of neutron matter in the cylindrically symmetric cell
Fig.4The distribution of energy density of neutron matter in the spherically symmetric cell
.
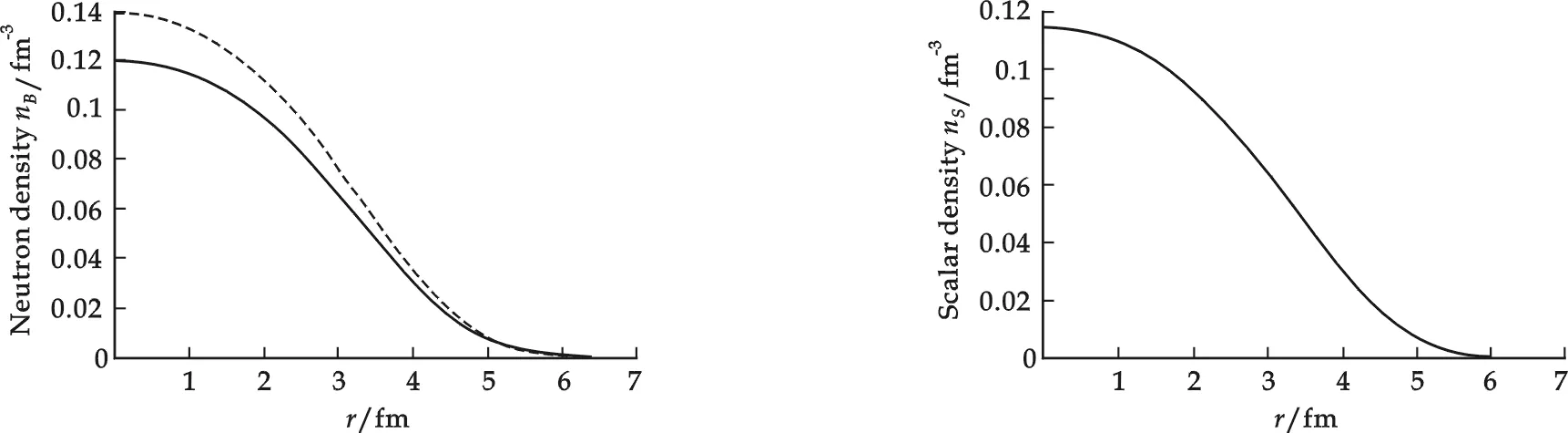
Fig.5The distribution of neutron density in the spherically symmetric cell that the average density is about0.03fm-3
Fig.6The distribution of scalar density of neutron matter in the spherically symmetric cell
2.2 The spherically symmetric cell
In the spherically symmetric cell, the Eq.(10) can be reduced to:
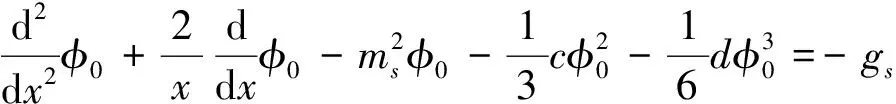
(33)
and the boundary condition is the same with Eq.(31, 32).
The energy density, neutron density and scalar density of neutron star matter in the spherically symmetric cell are shown in Fig.4~Fig.6. And the energy density and neutron density become zero atr= 6.73 fm. Comparing Fig.1 to Fig.4, Fig.2 to Fig.5 and Fig.3 to Fig.6 we can see that rotation impose similar influences on these three quantities of neutron star matter in two types of cells. However, the three quantities and maximum radius in spherically symmetrical cell are greater than the counterparts in cylindrically symmetrical cell in the same condition.
3 Summary
By the relativistic mean field model and Thomas-Fermi approximation we have studied the energy density etc. of neutron matter in the cylindrically symmetric cell and spherically symmetric cell, respectively. The cell is assumed to be in the surface of neutron star with radius of 12 km and rotating with a period of 1.337 s, 0.09 s and 0.5 ms. It is found that the rotation impose significant influence on the energy density, the neutron density but not on the scalar density when the period is 0.5 ms. On the other hand, all calculated quantities of spherically symmetric cell are greater than that of cylindrically symmetric cell. We assume that the cell is only composed of neutrons for simplicity, and we will consider the proton and electron in the cell in our next work.
[1] Henning. Heiselberg,Morten Hjorth-Jensen. Phases of dense matter in neutron stars[J].Phys. Rev.,2000,328:237-327.
[2]R. C. Tolman. Static solutions of Einstein′s field equations for spheres of fluid[J]. Physical Review,1939, 55(4): 364-373.
[3] J. R. Oppenheimer, G. M. Volkoff. On massive neutron cores[J]. Phys. Rev., 1939,55: 374-381.
[4]A. Hewish, S. J. Bell, J. D. H. Pilkington,etal. Obervation of a rapidly pulsating radio source[J]. Nature, 1968,217: 709-713.
[5] F. Pacini. Energy emission from a neutron star[J]. Nature, 1967, 216:567-568.
[6]M. Prakash, J. Lattimer, J. A. Pons,etal. Reddy, evolution of a neutron star from its birth to old age[J].Lect. Notes Phys.,2001,578:364-423.
[7]W. David. Arnett , Richard. L. Bowers. A microscopic interpretation of neutron star structure[J]. Astrophysical Journal Supplement, 1977, 33: 415-436.
[8]Benjamin J. Owen, Lee Lindblom, Curt Cutler,etal. Gravitational waves from hot young rapidly rotating neutron stars[J]. Phys. Rev., 1998, 58: 84-90.
[9]H. Shen, H. Toki, K. Oyamatsu,etal. Relativistic equation of state of nuclear matter for supernova and neutron star[J]. Nucl. Phys., 1998,A637: 435-450.
