Borel-Cantelli引理的一个推论
2010-02-23王福彪
陕西科技大学学报 2010年6期
王福彪
(南京财经大学数学学院, 江苏 南京 210046)




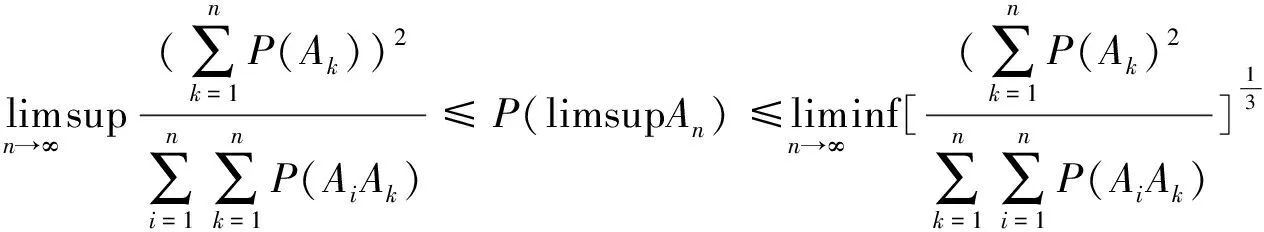
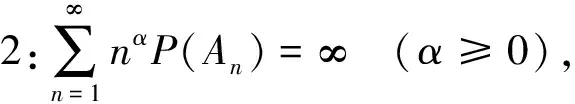
在证明定理2之前首先证明一个引理.


(1)



定理2的证明先证左边不等式,由Cauchy-Schwarz不等式得

由引理得以下不等式


参考文献
[1] Chungrong Feng, Liangpan Li, Jian Shen.On the Borel-Cabtelli lemma and its generalization[J]. C.R.Acad.Ser.,2009,347:1 313-1 316.
[2] XIE Yuquan.Abilateral inequality on the Borel-Cantelli lemma[J]. Statist.Probab.Lett., 2008,78:2 052-2 057.
[3] Hu Shuhe,Wang Xuejun,Li Xiaoqin,etal.. Comments on paper:a bilateral inequality on the Borel-Cantelli lemma[J].Statist.Probab.Lett., 2009,79:889-893.
[4] Petrov.V.V. A generalization of the Borel-Cantelli lemma[J]. Lett, 2004,(67):233-239.
[5] Kochen-Stone. A note on the Borel-Cantelli lemma[J]. Illinois Journal of Mathematics,1964,8:248-251.
