图形变换在标志设计中的应用
2010-02-23徐人平
翟 颉, 徐人平
(昆明理工大学机电工程学院, 云南 昆明 650093)
0 引言
标志,在视觉上就是一种表明事物特征的形象记号,是通过人所具有的知觉、思维、记忆、情感等作用而得以认知的.由于设计作品存在艺术性和多样性等特点,因此其设计过程没有固定的模式和方法,但变化之中仍有许多基本规律和共同原理可以遵循.标志设计的实质,就是进行图形变换,通过图形变换达到符合审美的设计标准.在标志设计中,这种共性的审美因子,除了人所共知的图形图像所表现的意义之外,主要是指人所共有的基本平衡感、节奏感、韵律感等.一方面,这些秩序美是审美的感受;另一方面,它们也是重要的造型手段.图形变换的合理利用有助于反映和表现标志设计的主题内容,增强标志设计的美感[1-3].
平衡,是形态秩序再造所要达到的最基本要求,是一种可视量和非可视量在质与量上的对比与和谐的关系,它不仅将节奏感、韵律感融合于对称美之中,还巧妙地将有规律的共性与富有创意的个性融汇于作品之中,因此在标志设计中得到了广泛使用.毕达哥拉斯学派指出“和谐是数的结构,它是最重要的数的规定性,它规定事物,使事物能够被认识;和谐是最美的.”任何一个物体都可以看作是一定数量的点按一定规律排列的集合,所以我们在研究物体与表示其图形之间的关系时,可以将其归结为研究物体上任意一点的坐标与该物体图形上对应点坐标之间的关系,而这种坐标之间的联系及其坐标的变换就是我们所说的图形变换.这些变换可以是图形的对称变化、旋转变化和平移变化,也可以是回转变化等,它们都可以用矩阵的方法进行表现,同时也正是标志设计中最常见的造型手段,给人以平衡的视觉感受.图形变换的矩阵方法是图形数字化处理的最佳方式,也是计算机绘图的数学基础和重要手段.掌握图形变换的矩阵知识对分析标志设计中的图形关系具有非常重要的作用[4,5].
矩阵理论是线性代数的重要组成部分,它的概念和运算法则是研究构成艺术必不可少的工具之一,应用得当可以对图形进行空间上的变换,并对标志设计起到积极的作用[6].
1 矩阵在标志设计中的作用
标志设计,在操作上就是根据载体的需要,将图形的内部结构通过外部形态表现出来.虽然审美的心理过程存在着较大的主观性差异,但审美也具有超越个性与地域文化特征的共性因子,体现在图形上就是指人所共有的基本平衡感,它既是审美表现的基本目的,又是造型活动的基本思路.通过数字运算,运用矩阵的理论,合理地将点、线、面排列、组合并巧妙地将其安排在标志设计当中则能更准确、更便捷的呈现出其审美特征,使得图形数字化,因此清楚地分析其图形关系,对计算机图形学也具有十分重要的意义.
在标志设计的造型活动中,每当画面中新增一个点、一条线、一个块面,或者是改变了原有形态的排列组合方式,就会在画面原有的视觉关系基础上又增加多层次、多角度的视觉变化关系.一般情况下,标志设计中所使用的视觉元素越多,画面视觉关系就越复杂,在矩阵运算上也就越复杂,它需要几种矩阵变换相叠加而最终得出所需要的图形.
众所周知,任何一个物体都可以看作是一定数量的点按一定规律排列的集合,它们都可以用某些图形来表示,所以我们在研究物体与表示其图形之间的关系时,可以将其归结为研究物体上任意一点的坐标与该物体图形上对应点坐标之间的关系,而这种坐标之间的联系及其坐标的变换就是我们所说的图形变换.根据需要,任何二维或是三维的图形,都可通过变化而形成新的图形,这些变换可以是图形的对称变化、旋转变化和平移变化,也可以是回转变化等.它们也正是标志设计中最常见的造型手段,给人以平衡的视觉感受,这些都可以用矩阵的方法进行表现.
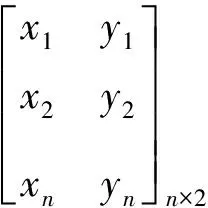
这样就建立了平面图形的数学模型.
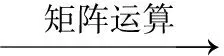
图形变换的实质就是研究图形之间所对应的构成关系,这种关系决定着设计作品是否美观且具有注目性.作者在文献[7]中已指出这种有秩序的图形关系对标志设计起到了十分积极的作用.要想使作品具有韵律感和节奏感,满足人们审美的基本平衡感,在设计过程中就应当把体现对称美作为造型设计的基本思路,这种造型方法在自然科学中就是我们所说的矩阵变换,为了使图形在计算机中达到反射对称、回转对称、旋转对称、移动对称等图形变换,使图形具有有力的节奏感,并产生高度统一的秩序感和较强的视觉冲击力,就要利用矩阵的方法使图形数字化,最终能够更好、更容易地进行标志设计,使其满足人们的审美需求.
2 标志设计中的矩阵变化
平衡,是客观世界本质规律在设计中的反映,也是人类在现实中赖以生存的基本生理感觉之一.在标志设计中,平衡是构成设计整体协调的基本保证,可以给人以舒服的视觉享受和安全感.我们所研究的以静感为主导的平衡是指:以对称性原理构成的形态平衡关系,也称之为均齐.依据对称关系的不同特点,又可将视觉形态对称的形式分为反射对称、回转对称、旋转对称、移动对称4种主要类型.就标志设计而言,其运用十分广泛,它在知觉上表现出以静为主,静中有动的特点,在形态特征上具有重复性和理性且装饰性强的特点,通常给人以典雅、高贵、和谐、可信任的感受,容易取得审美的和谐与满足.
2.1 反射对称
反射对称也称为轴对称.反射对称的特点是,当以一条中心轴划分形态时,中心轴两侧的形态可呈现出一种完全对称重合的“镜像反应”关系,这种对称形式在标志设计中应用十分广泛.由于它是一种在对称轴两侧以等量和等形的精确平衡为特征所构成的绝对对齐形式,所以在各种平衡的形式中是一种呼应关系最严谨、稳定感最突出的平衡形式,在标志中有利于表现庄重、稳定、严肃、成熟、安静等主题的设计.依据形体关系中对称轴的方向和数量,反射对称还可分为竖轴反射、横轴反射、斜轴反射和多轴反射,如表1所示,我们可以看出,在同一形态关系中,对称轴的数量越多,平衡感越强.用矩阵的方式表示如下.
2.1.1 竖轴反射
当竖轴为Y轴时,关于Y轴对称变换,点对Y轴对称,应有x′= -x,y′=y,则变换矩阵为:
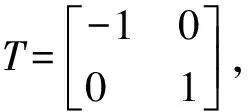
(1)
2.1.2 横轴反射
当横轴为X轴时,关于X轴对称变换,点对X轴对称,应有x′=x,y′= -y, 则变换矩阵为:
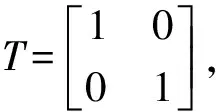
(2)
2.1.3 斜轴反射
横轴为X轴时,关于+45°线的对称变换,点对+45°线对称,应有x′=y,y′=x,
(3)
2.1.4 多轴反射
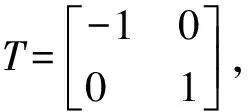
(4)
2.2 回转对称
回转对称是由反射对称演化而来的一种对称形式,虽然其对称轴两侧的形态是等量、等形、相对呼应的,但在对称轴两侧的形态动势是以头尾相反的方向安排的.在这种对称方式中,由于运动方向的强烈矛盾,导致整个标志的造型产生明显的跳跃感,它既能保持形态相互呼应的对称特征,又能在整体的对称关系中构成较强运动感的平衡形式.如表2所示,依据回转对称的方向特征也可分为竖轴回转、横轴回转、斜轴回转和曲轴回转4种组织方式,用矩阵的方式表示如下.
2.2.1 竖轴回转
(1)首先将图形的基点平移到原点上,然后绕基点(原点)旋转180°后,再将基点平移回原位,则变换矩阵为:
(5)
(2)接着将(x,y)扩展为(x,y, 1),并将图形在y向上平移一个单位图长m,得出变换矩阵为:
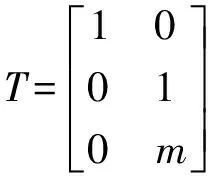
(6)
2.2.2 横轴回转
(1)首先将图形的基点平移到原点上,然后绕基点(原点)旋转180°后再将基点平移回原位,则变换矩阵为公式(5).
(2)接着将(x,y)扩展为(x,y, 1),并将图形在x向上平移一个单位图长l,得变换矩阵为:
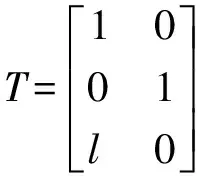
(7)
2.2.3 斜轴回转
(1)首先将图形的基点平移到原点上,然后绕基点(原点)旋转180°后再将基点平移回原位.
(2)将坐标轴旋转一个角度,并使这一斜轴与X轴或Y轴其中一轴相重合,并沿轴的方向平移一个图形长度l.
2.2.4 曲轴回转
(1)首先将图形的基点平移到原点上,然后绕基点(原点)旋转180°后再将基点平移回原位,.则得到相应的变换矩阵如公式(5)所示.
(2)沿轴方向平移一个长度l.
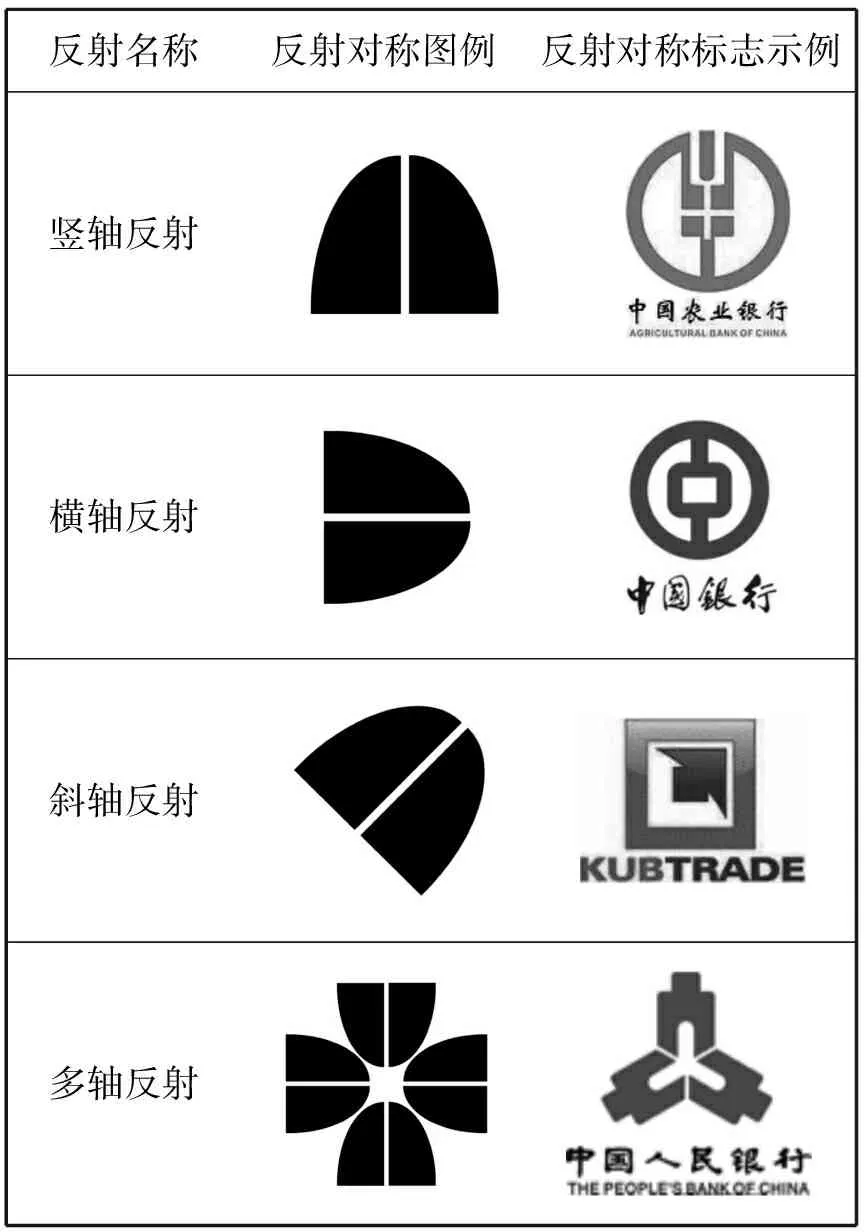
表1 反射对称图例

表2 回转对称图例
2.3 旋转对称
旋转对称是以一个点为中心,将对称轴按均等的角度呈放射状顺向重复排列,从而构成在视知觉中具有旋转运动趋势的对称秩序关系,这种视觉语法的造型关系运用于标志设计中一般采用2至6个对称轴,给人以规整、严谨之感而又不失内在的活力,可营造较强的注目性,如表3所示.用矩阵的方式表示如下:平面图形想要绕任意点,旋转任意角度,需要4个步骤,我们这里把任意点定义为0(x0,y0),旋转角度α分别为180°、90°、72°、60°.
(1)首先将旋转的中心点平移到原点,则变换矩阵为:
(8)
(2)接着将图形绕坐标系原点旋转一个角度α,变换矩阵为:

(9)
(3)再将旋转中心平移回到原来的位置,其变换矩阵为:
(10)
(4)最后得出绕任意点o的旋转变换矩阵为
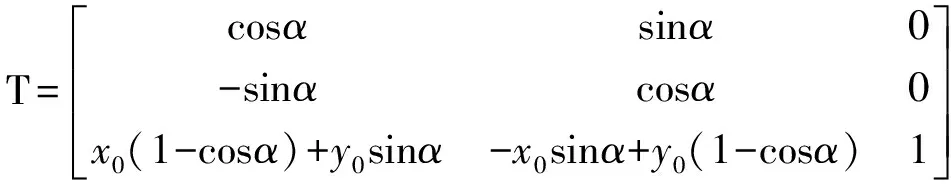
2.4 移动对称
移动对称是指通过等间距移动对称轴,使相同的单元形态有规则地重复排列,这种形态关系具有构成简便、节奏明晰且可无限重复的特点.如表4所示,移动对称可分为:横向移动、竖向移动、斜向移动和四向移动4种形式.用矩阵的方式表示如下:首先要对点向量进行扩充,将[xy]扩充为[xy1],即把点集矩阵扩充为n×3阶矩阵,这样点集矩阵与变换矩阵即可进行乘法运算,l,m分别为x,y方向上的平移量.
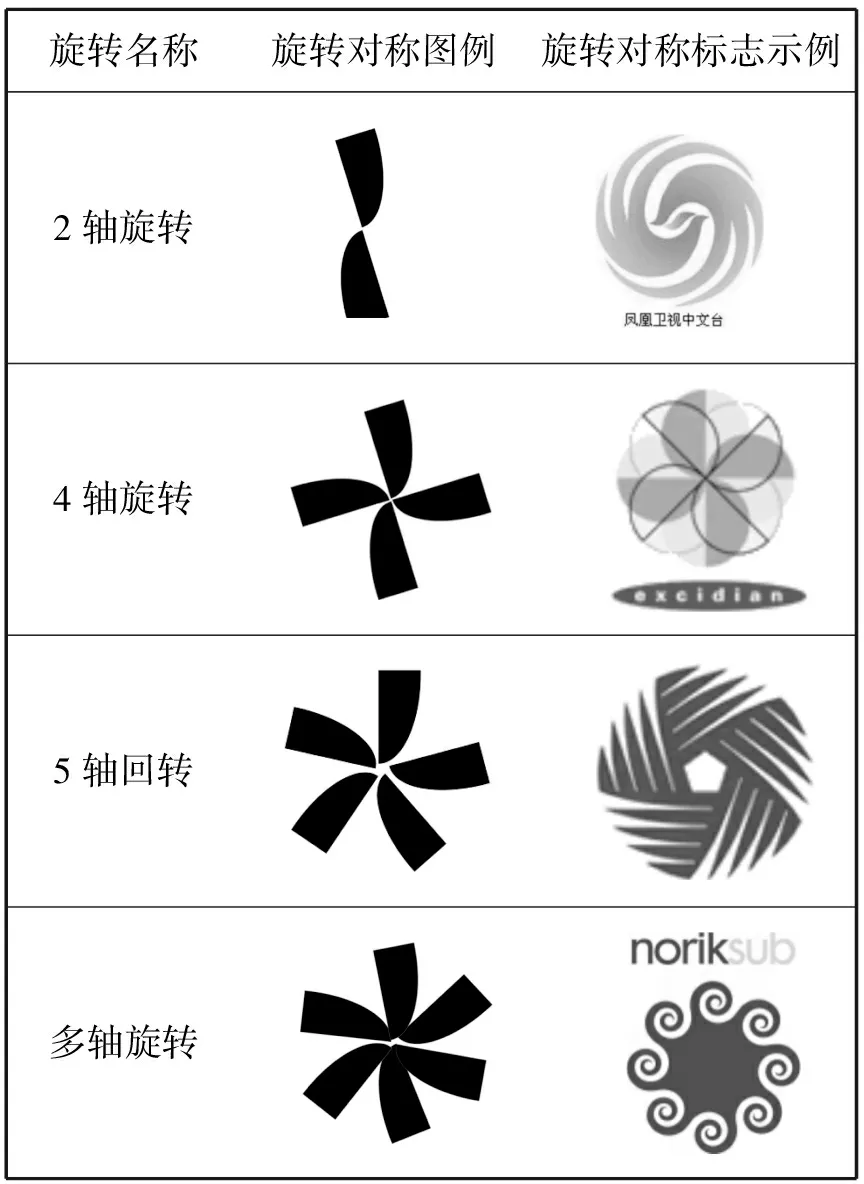
表3 旋转对称图例

表4 移动对称图例
2.4.1 横向移动
横轴为X轴时,图形在X方向上进行平移,则变换矩阵为公式(7).
2.4.2 竖向移动
竖轴为Y轴时,图形在Y方向上进行平移,则变换矩阵为公式(6).
2.4.3 斜向移动
图形首先在X方向上进行平移,得出变换矩阵为公式(7),再在Y向上进行平移,则变换矩阵为公式(6).
2.4.4 四项移动
图形首先在Y轴方向上进行平移,得出变换矩阵为公式(6),再在X向上进行平移,则变换矩阵为公式(7).
3 结束语
(1)研究物体上任意一点的坐标与该物体图形上对应点坐标之间的关系,就是我们所说的图形变换.矩阵理论应用得当可以对图形进行空间上的变换,并对标志设计起到积极的作用.
(2)标志设计的共性审美因子体现在图形上,就是指人所共有的基本平衡感,它将节奏感和韵律感很好地融合在一起,既是审美感受,也是造型活动的基本思路.
(3)平衡是形态秩序再造所要达到的最基本要求.依据对称关系的不同特点,又可将视觉形态对称的形式分为反射对称、回转对称、旋转对称、移动对称4种主要类型.对称美是符合审美规律的.
(4)任何一个物体都可以看作是一定数量的点按一定规律排列的集合,它们都可以用某些图形来表示.
(5)反射对称、回转对称、旋转对称、移动对称这些图形变换用矩阵的方式表现出来,应用于标志设计中可以使得标志设计手段更有章可循,设计作品更符合审美标准.
(6)图形变换的矩阵方法是图形数字化处理的最佳方式,也是计算机绘图的数学基础和重要手段.合理地将点、线、面排列、组合,巧妙的安排在标志设计当中,则能更准确、更便捷的呈现出其审美特征和图形关系,对计算机图形学也具有十分重要的作用.
[1]郭茂来.视觉艺术概论[M].北京:人民美术出版社,1999.
[2]王剑锋.标志构成新解[M].南宁:广西美术出版社,2004.
[3]张宪荣.设计符号学 [M].北京:化学工业出版社,2004.
[4]徐人平.设计数学[M]北京:化学工业出版社,2006.
[5]文 红.标志设计教程 [M].重庆:西南师范大学出版社,2004.
[6]苟双晓,徐人平.包装视觉语法 [J].包装工程,2006,27(5):10-12.
[7]翟 颉,徐人平.解读标志设计的秩序构成[J].东北农业大学学报,2009,7(6):63-66.
