岭估计图像重建算法中岭迹参数的多项式拟合研究

任变青， 潘晋孝， 孔慧华， 刘 宾

(1.中北大学数学系, 山西 太原 030051；2.中北大学信息工程系, 山西 太原 030051)

0 引 言

CT作为一种重要的测量手段，已经广泛地应用于医学、天文学、工业检测等领域.图像重建算法是CT研究中的一个主要领域，图像重建算法以滤波反投影算法(Filtered back projection, FBP)最具代表性，应用最广，但该重建算法最适宜于数据完全的场合.在许多实际情况下, 我们得到的投影数据常常是有噪声的，此时重建图像最常用方法是迭代法.在迭代算法中，代数重建算法(Algebraic reconstruction technique, ART)是提出最早并最为人们所熟悉的算法.迭代法也有缺点，就是计算量大和重建时间长，但随着计算机的发展，迭代算法重新受到了人们的青睐.

岭估计算法就是一种迭代算法，在实际中图像重建不完全投影数据对算法的依赖很大，得到的重建图像也有很大的区别，而岭估计算法对不完全投影数重建是一种好的算法.在本文中利用松弛参数的岭估计迭代算法对128×128 数字化的图像进行了仿真,又从45度观测角内得到的投影数据中重建图像并得到了较好的重建效果，同时在小范围内取不同的岭迹参数k值进行图像重建，比较了k值对图像重建的影响.由于实际求解参数的计算量是相当大的，分析参数和重建图像的均方差的关系得到它们之间的多项式拟合式，由它们之间的拟合式得到参数的好的取值范围.下面我们从算法的仿真数据来研究参数的拟合式.

1 迭代算法

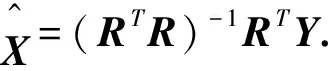
X(l+1)=X(l)+λ[RTY-(RTR+kI)X(l)]

(1)

这里岭迹参数k可由岭迹法等方法求得[2].X随着k取值的不同得到不同的估计.λ是松驰参数.为了叙述方便，引入记号：b=(bj)J×1=RTY,A=(aij)I×J=RTR+kI，则式(1)为

X(l+1)=X(I)+λ(b-AX(l))

(2)

其相应的松弛迭代公式的分量形式可取为

(3)

其中i=1,2,…,J；迭代次数l=1,2,….松弛参数λ可以取下面(4)所定义的，也可以适当选择松弛因子，使得迭代过程(3)收敛较快.

2 由数值仿真得到的参数与均方差的关系图

首先构造一个以像素为单位的128*128仿真图片[3]，做无噪声仿真研究如图1所示,松弛因子取为0.05，k取为不同的值.

图1 数值仿真(无噪声)

图1中, 迭代次数都为20次，(a)为无噪声原图；(b)为k=0.9, 128个探测单元的重建图像；(c)为k=0.8, 128个探测单元的重建图像；(d)为k=0.9, 128个探测单元的重建图像；(e)为k=1.2, 128个探测单元的重建图像；(f)为k=1.4, 128个探测单元的重建图像.

在仿真图片加入均值为0，方差为0.02的高斯噪声，用同样迭代方法作仿真研究，松弛因子λ仍取为0.05，k取为不同的值,得到图2.

图2 数值仿真(有噪声)

图2中，迭代次数都为20次，(a)为有噪声原图；(b)为k=1.0, 128个探测单元的重建图像；(c)为k=1.2, 128个探测单元的重建图像；(d)为k=1.4,128个探测单元的重建图像；(e)为k=1.6, 128个探测单元的重建图像；(f)为k=1.8, 128个探测单元的重建图像.

现比较重建图像的均方差，原图向量为X=(x1,x2,…,xJ)T，重建图像向量为Y=(y1,y2,…,yI)T，则均方差q=(xi-yi)2/n×n,其中i=1.2,…,n=128,比较k值对重建图像与原图的均方差影响.

图3描述了无噪声和有噪声图像重建的均方差和岭迹参数之间的关系, 无噪声重建k=0.9取得到最小的均方差, 有噪声重建取得到最小的均方差,由两者之间的关系可知在松驰参数一定的情况下,岭迹参数k存在最优值,使重建图像的均方差最小.

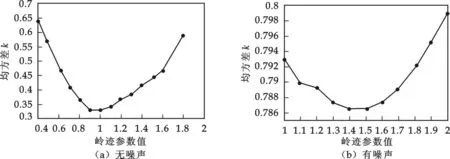
图3 均方差曲线图

由上面数值仿真结果可以看出，在只有45度的观测角内的投影数据时，无论是有噪声或无噪声仿真图片岭估计算法都能得到比较好的重建图像.在相同的迭代次数里，k值选取的不同会对图像的均方差有较大的影响,且岭迹参数k存在最优解,图3显示了岭迹参数选取的规律,也许用其它合适的数据可能会比本文中得到的重建图像好.需要指出，对于不同的重建图像和不同的松驰参数λ，k值选取也是不同的.

由图3可以看到岭迹参数与重建图像均方差之间存在一种可分析方程,类似于常见的二项式方程，下面对几种多项式拟合进行分析以确定用什么样的方程最合适.

表1 多项式拟合方程

下面对无噪声重建图像的岭迹参数与重建图像均方差做分析，由于两者关系的不确定性，我们对两者做多种分析，可能多项式拟合、指数拟合、对数拟合得到不同的结果，对3种拟合结果做比较得到合适的确定岭迹参数的恰当的方程.

相应的图如图4所示.

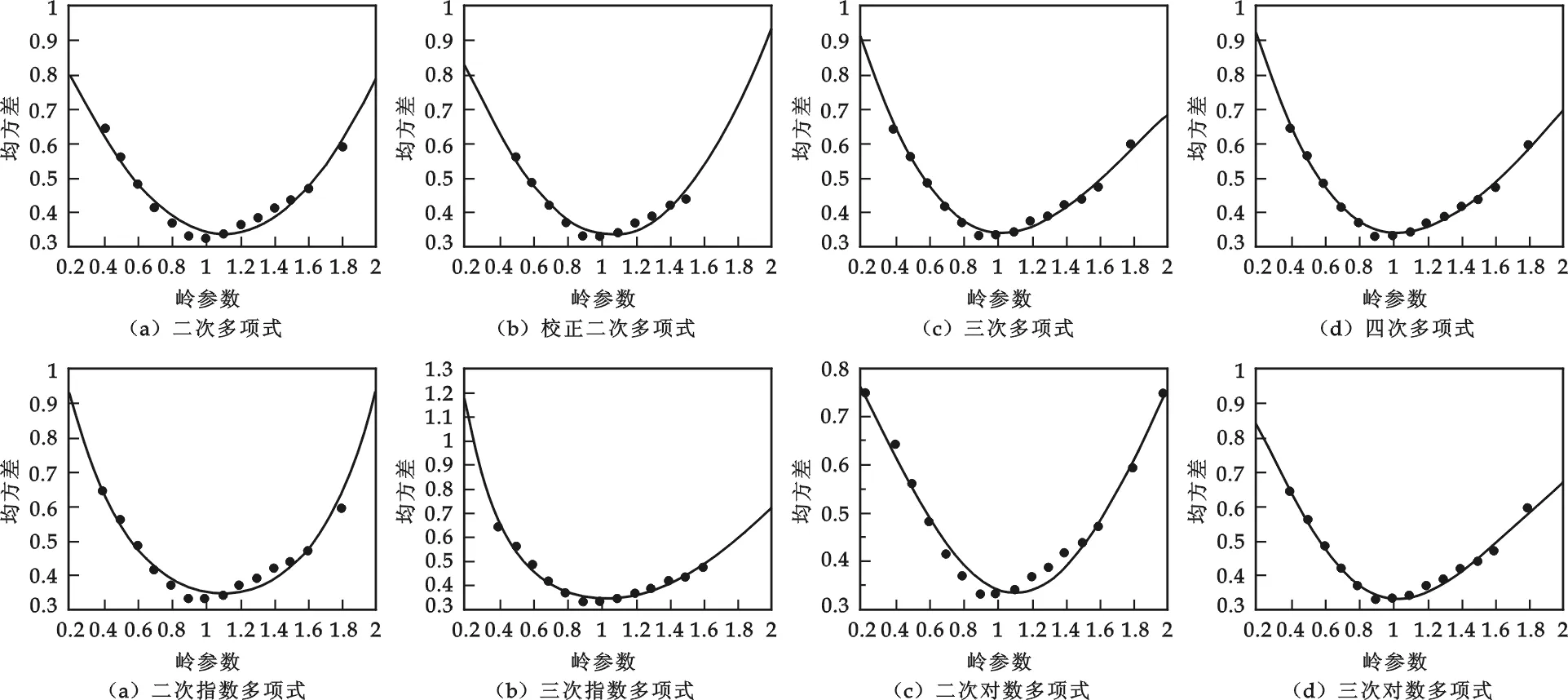
图4 多项式拟合曲线图

由图4可见,用多项式拟合能得到合适的拟合方程，其中三项式和四项式拟合得到了相同的标准差，就简单而言二项式拟合最为合适.就其实用性比较,二项式拟合已能很好的得到确定岭迹参数的拟合方程，可对无噪声和含噪声的重建图像做二项式拟合以确定恰当的岭迹参数.二项式拟合能很好的得到确定岭迹参数的拟合方程，从而确定合适的参数，加快了图像重建.

3 结束语

岭估计算法的计算量很大，图像迭代也比较慢,我们必须充分地利用先验知识,减少重建时间,在每一次的迭代中都采用一些技巧来加快收敛. 可以采用并行的CPU 进行运算, 使运算时间减少倍从而满足实时图像处理的需要.

由上述对投影数据重建的分析可知，在探测单元和迭代次数一定的情况下，k值的选取对图像质量有很大的影响.对于不同的重建图像和不同的松驰参数λ，k值选取是很重要的, 如果k值的选取不合适会使重建图像均方差相差很大.在本文中讨论了岭迹参数k在一定范围内存在最优解,由表1看出均方差和岭迹参数之间存在着一定的关系.对于理想状态的图像重建选取一定的k值即可,但对于含有噪声的实际情况的图像重建选取一定的k值就需要进行二项式拟合, 二项式拟合已能很好的得到确定岭迹参数的拟合方程，从而确定合适的参数，对图像重建起到了缩短重建时间的效果.

[1] 张 朋,张兆田.几种CT图像重建算法的研究和比较[J] .CT理论与应用研究,2001,10(4)：4-9.

[2] 潘晋孝,韩 焱.图像重建的岭估计算法[R].合肥:中国电子学会第八届青年学术年会,2002.

[3] 缪丽娜,潘晋孝,韩 焱.探测器和投影数目对CT 重建精度的影响[J].测试技术学报,2002,(4):302-304.

[4] H.Malcolm Hudson,Richard S.Larkin . Accelerated image reconstruction using ordered subset of projection data[J] .IEEE Transaction on Medical Imaging,1994,13(4):601-609.

[5] Dan J.Kadrmas. Statistically regulated and adaptive EM reconstruction for emission computed tomography[J]. IEEE Transaction on Nuclear Science,2001,48(3):790-798.

[6] 刘 亮，潘晋孝，任变青. 一种基于FDK的锥束CT重建的改进方法[J]. 光散射学报, 2007,(1). 91-95.