DSSS 信号混沌检测方法的研究
2010-02-23兀旦晖
兀旦晖
(陕西科技大学电气与信息工程学院, 陕西 西安 710021)
0 引言
DSSS(直接序列扩频)通信是一种具有优良抗干扰能力的新型通信方式,由于它是用一个高速的伪随机序列与信息数据码相乘后通过载波调制发射出去的,以展宽并降低信号功率谱的一种先进的通信体制,具有能获得多址接入及低截获概率特性、抗干扰特性和强保密性等优点,因此在军事通信、卫星通信、移动通信等系统中得到了广泛的应用.开展对 DSSS 信号检测方法的研究在许多领域具有重大的现实意义,在环境噪声较强烈的情况下,利用传统的检测和参数估计方法一般会失败,为此迫切需要寻找新的方法以解决该问题.
目前,Duffing 振子用于微弱周期信号检测已取得了很多成果[1-4],作者首次把 Duffing 振子成功地应用到非周期的微弱 DSSS 信号的检测上.本文分析了Duffing 振子对方波调制信号的敏感性,通过对方波调制信号检测过程中出现的间歇混沌现象的分析,推导出检测微弱 DSSS 信号的方法,仿真结果验证了该理论分析的正确性和所提方法可以检测出信噪比-20 dB 以下的微弱 DSSS 信号的有效性, 为DSSS信号检测提供了一种高效的新途径.

图1 系统检测框图
1 Duffing 振子对方波调制信号的敏感性
本文先研究混沌临界状态的 Duffing 振子对方波调制信号的敏感性,为微弱DSSS 信号检测做准备.检测框图如图1 所示.
Duffing方程的具体形式如下[5]:x″+kx′-x3+x5=fcos(t)+input.其中:input=s(t)+n(t),n(t)为噪声,s(t)为外界有用信号.
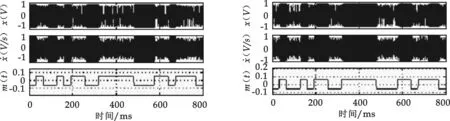
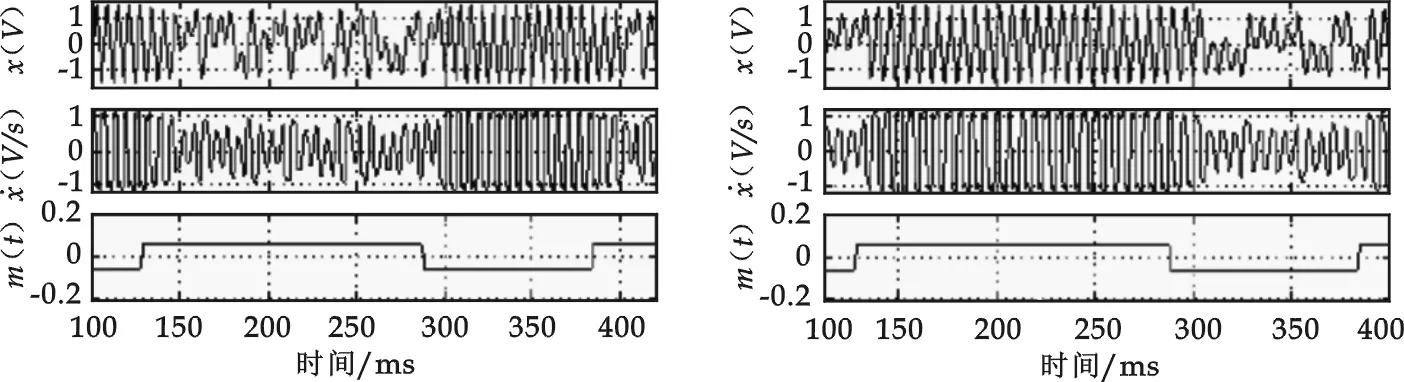
设输入信号:s(t)=au(t)cos(ωt),a< p(t)=frcos(ωt)+au(t)cos(ωt)=F(t)cos(ωt) 其中,策动力幅值F(t)=fr+au(t). 从而系统状态是否改变关键在于F(t)和fr的关系:F(t)>fr,系统处于大尺度周期状态;F(t) (1)u(t)=1,F(t)=fr+a>fr,系统处于大尺度周期状态. (2)u(t)=1,F(t)=fr-a 研究发现满足条件a< 当信号满足a< 待检测的 DSSS 信号形式为: 则混沌临界状态的 Duffing 系统总策动力为: =F(t)cos(ωt+θ(t)) 其中 从而推出Δω=0时: 对于 DSSS 号,m(t)是-1,1无规律交替出现的,因此系统的运动状态也应该是混沌和大尺度周期交替出现,即应出现间歇混沌现象.再由前面分析可知,要使系统有足够的时间分别维持稳定的大尺度周期状态和稳定的混沌状态,至少需要 50/3 个周期的连续正弦信号.对于 DSSS 信号来说,一个码片内通常有十几个周期的正弦信号,并且会出现连续几个相邻的码片极性相同,因此要出现 50/3个周期的正弦信号是可能的,也就是从理论上说明了可以观察到较明显的间歇混沌现象. 仿真分析:fr=0.718 4,Δω=0,a=0.06,P=0.001 8. 图2 φ=π时的实验结果 图3 φ=0时的实验结果 图4 φ=π时结果部分放大 图5 φ=0时结果部分放大 图2是φ=π时,图3是φ=0时的仿真实验结果,图4是φ=π时结果部分放大图,图5是φ=0时结果部分放大图.最上面两个波形为加入DSSS 信号后系统的输出,它对系统作用的结果,导致了大尺度周期和混沌现象交替出现,主要特征体现为间歇混沌行为,第三个为调制前基带信号m(t)的波形.由图2 可知,当φ=π时,m(t)=-1,系统处于混沌状态,m(t)=1,系统处于大尺度周期状态;由图2 可知,当φ=0时,m(t)=1,系统处于大尺度周期状态,若m(t)=-1,当系统处于混沌状态,实验结果与上面理论分析一致. 从而,Δω≠0时,在相邻相同的码片内系统作初相不同的间歇混沌运动,运动周期T=2π/Δω. 仿真分析:Δω=0.001,σ=0.5,SNR≈-21dB,其它条件同上,仿真结果如图6所示.在实际情况中,一方面由于 DSSS 信号脉冲持续期比较短,另一方面又由于噪声的存在,导致了周期的不确定,但仍可以观察到较明显的间歇混沌现象,从而检测出微弱 DSSS 信号. 图6 利用 Duffing 振子检测微弱 DSSS 信号 图6(a)两波形为加入噪声后系统的输出,系统仍然保持混沌状态.图6(b)两波形为输入信噪比为-21 dB 的DSSS信号后,系统输出的时域曲线,它对系统作用的结果,导致了大尺度周期和混沌现象交替出现,主要特征体现为间歇混沌行为.系统输出时域曲线明显不同,从而将微弱 DSSS 信号检测出来. 本文分析了Duffing 振子对方波调制信号的敏感性,通过对方波调制信号检测过程中出现的间歇混沌现象的分析,推导出检测微弱 DSSS 信号的方法,仿真结果验证了该理论分析的正确性和所提方法可以检测出信噪比-20 dB 以下的微弱 DSSS 信号的有效性, 为DSSS信号检测提供了一种高效的新途径. [1] 李 月,杨宝俊,石要武.色噪声背景下微弱正弦信号的混沌检测[J].物理学报, 2003,52(3):526-530. [2] 李 月,杨宝俊,石要武. 纳伏级正弦信号的混沌检测方法研究[J]. 通信学报, 2003,(4): 25-30. [3]王冠宇,陶国良,陈 行.混沌振子在强噪声背景信号检测中的应用[J].仪器仪表学报,1997,18(2):209-212. [4]王冠宇,陈大军,林建亚.Duffing 振子微弱信号检测方法的统计特性研究[J].电子学报,1998,26(10):38-44. [5]兀旦晖.混沌系统同步在弱信号检测中的应用[J].计算机测量与控制,2007,15(11):1 468-1 469.2 DSSS 信号的混沌检测方法及仿真研究
2.1 Δω=0
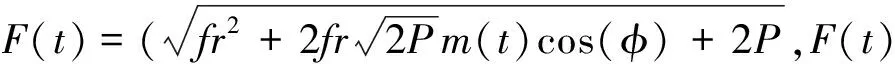
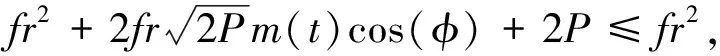
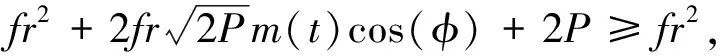
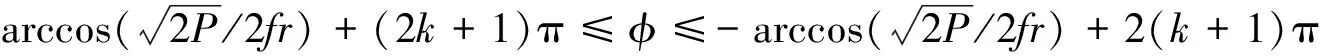


2.2 Δω≠0
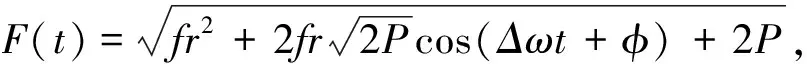
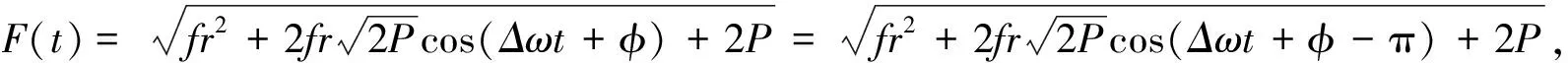

3 结束语
