基于广义回归神经网络G RNN 的矿井瓦斯含量预测
2010-02-13王文才王瑞智孙宝雷王政委
王文才 王瑞智 孙宝雷 王政委 刘 海
(1.内蒙古科技大学资源与安全工程学院,内蒙古 014000;2.东辰煤炭有限责任公司,内蒙古 010300)
1 广义回归神经网络
广义回归神经网络 (GRNN)是美国学者DonaldF.Specht在1991年的,其基础为数理统计,它能够根据样本数据逼近其中隐含的映射关系,即使样本数据稀少,网络的输出结果也能够收敛于最优回归表面,已在系统辨识和预测控制等方面得到应用。
1.1 GRNN原理
广义回归神经网络 (GRNN)是一种径向基(RBF)神经网络,是基于人脑的神经元细胞对外界反映的局部性而提出的,是一种新颖而有效的前馈式神经网络,它不仅具有全局逼近性质,而且具有最佳逼近性质。它由3层构成:输入层节点只传递输入信号到隐层,隐层节点由像高斯函数那样的辐射状作用函数构成,而输出层节点通常是简单的线性函数。隐层节点中的作用函数 (基函数)对输入信号将在局部产生响应,当输入信号靠近基函数的中央范围时,隐层节点将产生较大的输出,所以GRNN具有极强的局部逼近能力。其基本原理简述如下:
设j维向量为过程的输入向量,与其相应的输出向量为。GRNN通过计算给定时的条件数学期望来进行回归。GRNN估计和的联合概率密度函数,来建立一个估计的概率模型。通过训练输入输出数据集,利用非参数密度估计 (Nonparametric Density Estimation,NDE)法构建PDF估计器。给定x并假设被估计函数是连续光滑的,则y的期望值可以被估计为:
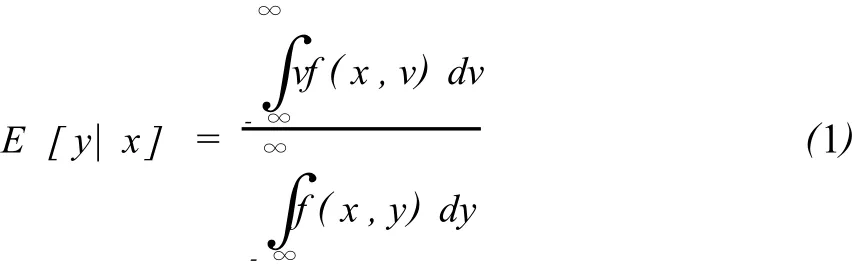
函数f(x,y)可定义为:

其中 xi和yi分别表示第i个训练输入向量和相应的输出,σ表示高斯概率密度函数 (Gaussian PDF)的宽度,也称为光滑因子。给定 x,则相应的回归估计可以确定为:
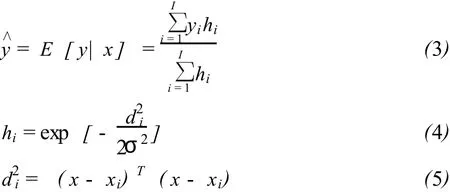
其中 hi表示高斯径向基函数,d2i表示向量x和向量xi之间的欧式距离的平方。
1.2 广义回归神经网络模型
GRNN的理论基础是非线性回归分析,是建立在非参数估计的基础上的一种非线性回归的径向基神经网络。它不需要事先确定方程形式,而是以概率密度函数替代固有的方程形式。也就是说它从观测样本里求得自变量和因变量之间的联合概率密度函数之后,直接计算出因变量对自变量的回归值。由于其非线性映射能力强,并且网络最后收敛于样本量聚集较多的优化回归面,因此通常应用在函数逼近、模式分类方面。GRNN的拓扑结构如图1所示,包括输入层、模式层、求和层与输出层等4层神经元。网络输入为 X= [xi,x2,…,xm]T,其输出为 Y= [y1,y2,…,Yl]T。

图1 广义回归神经网络拓扑结构
GRNN算法描述如下:
(1)把样本数据送入输入层。输入层单元数等于训练样本输入向量的维数 m,各单元是简单的分布单元,直接将输入向量的各元素传递给模式层。
(2)模式层的神经元数目等于学习样本的数目n,各神经元对应不同的样本。模式层中神经元 i的传递函数为i=1,2,…,n,其中,X为网络输入变量,Xi为神经元i对应的学习样本,σ为平滑参数。
(3)求和层包括2种类型神经元,其中一种神经元对所有模式层神经元的输出进行算术求和,模式层各神经元与该神经元的连接权值为1,其传递函数为其他神经元对所有模式层神经元的输出进行加权求和,模式层中第 i个神经元与求和层中第j个求和神经元之间的连接权值为第i个输出样本Yi中的第j个元素yij,求和神经元 j的传递函数为
(4)输出层中的神经元数目等于学习样本中输出向量的维数 l,各神经元将求和层的输出相除,即 yj=Sj/SD,j=1,2, …,l。
因而对于GRNN,一旦确定了训练样本,那么网络结构以及各神经元之间的连接权值也随之确定,影响网络输出的唯一因素是平滑参数σ。从而网络的学习完全依赖于样本数据,可最大程度地避免人为主观假定对预测结果的影响。并且GRNN根据样本数据逼近其中隐含的映射关系,甚至在样本数据少时网络的输出结果也能够收敛于最优回归表面,而且在结构方面也具有高度的并行性,从而可以大大提高网络的训练速度,能改善拟合的精度。
2 影响煤层瓦斯赋存的地质因素及其取值
影响煤层瓦斯赋存及分布的因素是多种多样的,通过对瓦斯地质规律的研究可知,影响煤瓦斯含量和分布规律的地质因素主要有:煤层埋藏深度、地质构造、煤层顶底板岩性、煤层厚度和煤的变质程度等。为了研究各因素与瓦斯赋存的关系,便于建立预测数学模型,把地质构造、顶底板岩性等定性化描述的因素,根据其本身的特性和对瓦斯赋存的影响进行科学地量化,转化为定量因素。
2.1 煤层埋藏深度
煤层的埋藏深度越深,煤层中的瓦斯向地表运移的距离就越长,散失就越困难。同时,深度的增加也使煤层在上覆压力的作用下降低了透气性,有利于保存瓦斯。在研究区内新生界直接不整合在二叠系上石盒子组煤系之上,中间的地层全部缺失,影响煤层瓦斯含量应与不整合面 (即基岩面)距煤层以下的深度有较大关系,因此煤层埋深因素取值为各钻孔13-1煤层顶板距基岩面的距离。
2.2 地质构造
地质构造中的断层破坏了煤层的连续性,使煤层瓦斯排放条件发生了变化,张扭性断层有利于瓦斯的排放,压扭性断层对瓦斯的排放起阻挡作用,成为逸散屏障。褶曲类型和褶皱复杂程度对瓦斯的赋存有影响,封闭的背斜有利于瓦斯的存储,是良好的储气构造。
由于井田内次一级褶皱构造不发育,所以在研究区内考虑地质构造因素时,主要考虑断层因素。据地质资料统计,研究区断层中张扭性断层54条,压扭性断层21条。由于区内断层众多,考虑到断层对瓦斯的赋存影响程度不同,在对断层因素进行参数量化时,以落差大于10m,水平延伸大于500m,切割13-1煤层至基岩面的断层作为统计依据,分别统计各钻孔距见煤点最近的张扭性正断层的水平距离作为构造参数。
2.3 煤层顶、底板岩性
煤层生成的瓦斯在漫长的地质年代有不同程度的遗散,而瓦斯的遗散与煤层围岩有密切关系。当煤层的顶、底板岩性为致密完整的岩石,如泥岩、油页岩时,煤层中的瓦斯比较容易保存;顶板为多孔隙或脆性裂隙发育的岩石,如砾岩、砂岩,瓦斯就容易逸散。研究区内13-1煤层顶、底板岩性主要有泥岩、炭质泥岩、砂质泥岩、粉砂岩和中砂岩。根据研究区顶、底板岩性特征,综合考虑含砂率和砂质颗粒粒度大小对顶、底板岩性因素进行量化,把粒度最大、含砂率最高的中砂岩记为1,含砂率最低的泥岩记为5,粉砂岩、砂质泥岩、炭质泥岩分别记为2,3,4。
2.4 煤层厚度
煤层的厚度与瓦斯的分布有一定的关系,一般说来,同一煤层随着厚度的增加,瓦斯生成量变大,瓦斯含量增加。区内钻孔13-1煤层厚度1143~6139m,平均4125m,煤层结构较复杂,半数以上见煤点有1~2层夹矸。煤厚因素取钻孔取煤的真厚,包括煤的厚度和夹矸的厚度。
2.5 煤的变质程度
在成煤的变质阶段,成煤的有机物在地层深处的高温、高压作用下,随着煤化程度的加深,固定碳增加,挥发分因转化成瓦斯而减少,瓦斯生成量增多。煤的变质程度可以用挥发分表示,所以在研究中以挥发分来表示变质程度因素。
2.6 其他地质因素的影响
研究区内煤层煤质变化不大,在总体上对瓦斯含量的变化影响可以忽略。而且煤系水文地质条件较为简单,未见地下水对煤层瓦斯赋存具有明显影响的块段,因此在预测模型中可以忽略这些因素。
3 基于 GRNN神经网络的煤层瓦斯含量预测
3.1 预测模型的构建
根据对煤层瓦斯含量影响因素的分析,这里分别取煤层埋藏深度、煤层厚度、地质构造、煤层顶底板岩性和煤变质程度等6项指标作为网络输入,煤层瓦斯含量作为网络输出,构建GRNN模型。如图2所示。
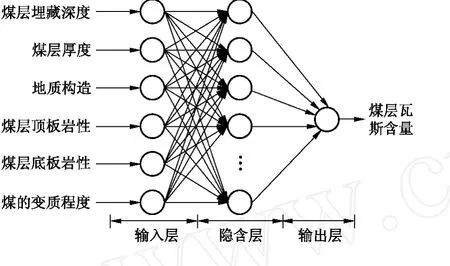
图2 GRNN网络结构模型
3.2 样本的选取和训练数据的归一化
根据已确定的网络输入和输出因子,选取某矿瓦斯含量的钻孔资料分别为训练样本,各指标数据见表1所示。
为取得比较好的预测效果,一般在训练网络之前都会将原始数据作预处理,本文采用了归一化处理对表1数据进行处理,网络训练好后,验证数据也需要作归一化处理才能输入网络,然后对网络输出作反变换,即将输出变量还原到原来单位。通常可在输入层用式 (6)将数值换算为 [0,1]区间的值,在输出层用式 (7)将数值换回。

式中—归一化后数据;
xi——未归一化数据;
xmin——数据变化的最小值;
xmax——数据的最大值。
归一化处理结果见表2所示。
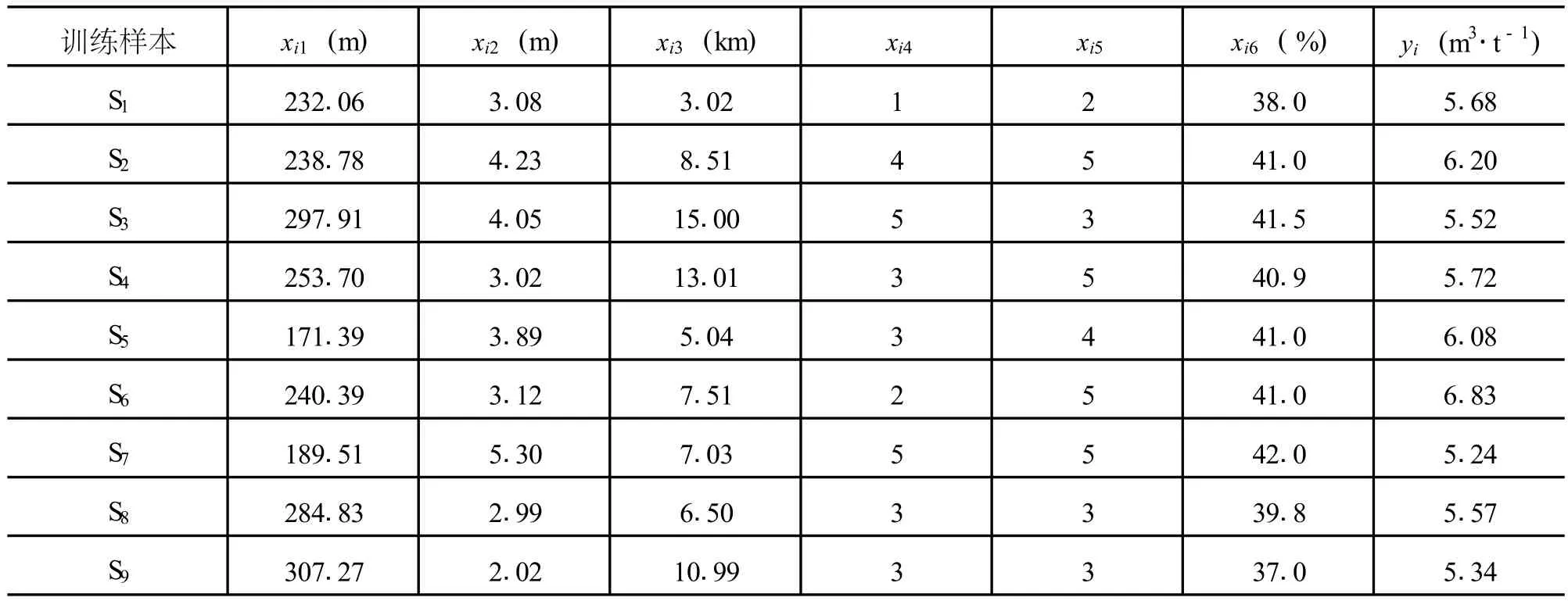
表1 某矿13-1煤层瓦斯含量及控制因素

表2 归一化处理结果

续表
3.3 神经网络的样本训练和测试
选取S1~S7作为训练样本,S8~S9作为测试样本。在本模型中,将光滑因子分别设置为0.4,此时网络的测试输出为:

经过反归一化处理后,实际结果为:

3.4 神经网络预测结果分析
由预测结果和实际数据比较可知,网络的预测误差比较大,这是因为网络模型的建立是以大量样本资料为基础的,本例中训练样本容量较小,所以预测精度不是很高。考虑到这些因素,这里的预测结果还是可以接受的。
4 结论
(1)文中建立了广义回归神经网络瓦斯含量预测模型,应用MAT LAB7.0人工神经网络工具箱编写了瓦斯含量预测程序,对多个样本数据进行了测试,由于训练样本容量较小,预测精度不是很高。考虑到这些因素,这里的预测结果尚可接受,也说明运用广义回归神经网络进行评价具有可行性。
(2)研究矿井瓦斯地质因素与煤层瓦斯含量的关系,是利用神经网络技术进行瓦斯含量预测的前提和基础工作,分析后确定煤层埋深、煤层厚度、顶板岩性和构造是影响煤层瓦斯含量的主要因素。
(3)利用人工神经网络建立的煤层瓦斯含量预测模型,克服了传统数学计算方法精确建模的困难,能够真实反映瓦斯含量与地质因素之间复杂的非线性关系。它为煤层瓦斯含量提供了一种新的预测途径。
[1] 吴观茂,黄明,李刚等.基于RBF神经网络的瓦斯含量预测研究 [J].煤炭科学技术,2008(1).
[2] 俞启香.矿井瓦斯防治 [M].徐州:中国矿业大学出版社,1992.
[3] 王生会.煤层瓦斯含量的主要控制因素分析及回归预测 [J].煤炭科学技术,1997(9).
[4] 飞思科技产品研发中心.神经网络理论与MAT LAB7实现 [M].北京:电子工业出版社,2005.
