新型超声变幅杆的优化设计

谨亚辉,轧 刚

(太原理工大学机械工程学院,山西太原 030024)

超声加工装置一般由超声发生器、换能器、变幅杆和工具头组成。在超声振动系统工作过程中,由超声换能器辐射面所产生的振幅较小,只有几微米,而超声加工所需要的振幅大约为几十至几百微米,这就需要通过变幅杆的放大与聚能作用将机械振动质点的位移量和运动速度放大,并将超声能量集中在较小的面积上。超声变幅杆的性能主要是由变幅杆的共振长度 L、放大系数 M P、形状因数 φ、位移节点 x、输入力阻抗Z等参数加以描述的[1]。变幅杆的合理设计必须既能满足以上各性能要求,保证超声波加工,又能满足变幅杆材料的强度要求。传统的超声振动系统的设计主要依据解析法,从经典理论出发,建立其动力学微分方程,根据边界条件确定其解。随着有限元理论的完善和相关应用软件的发展,根据ANSYS有限元分析软件可对变幅杆进行模态振动分析及谐响应分析,并在此基础上进行优化,设计出一种优于传统形状的新型变幅杆。

1 变幅杆的动力学分析

变幅杆的优化分析过程是建立在动力学分析基础上的。通过对变幅杆进行模态分析,找到在系统激振频率范围内的固有频率,然后,在该频率下对变幅杆进行谐响应分析,得出变幅杆自由端面的振幅、位移节点和最大等效应力,从而计算出放大系数M P、形状因数等性能参数。其中放大系数是指变幅杆工作在共振频率时,输入端与输出端的质点位移或速度的比值;形状因数φ是衡量变幅杆所能达到的最大振动速度的指标之一,它仅与变幅杆的几何形状有关,φ值越大,通过变幅杆所能达到的最大振动速度也越大。输入力阻抗Z定义为输入端策动力与质点振动速度的复数比值。然后再根据各性能参数不同特点来作为优化设计中的设计变量,状态变量或目标函数。

1.1 变幅杆的建模过程

变幅杆为半波长圆截面杆,工作频率为 15 kHz,大端直径D1=70 mm,小端直径D2=25 mm,材料为45钢,表1是45钢的材料参数。

表1 45钢的材料参数

变幅杆是轴对称的回转体,所以可用二维轴对称模型来求解,建模采取由点到线再到面,横截面母线由6点插值3次样条曲线构成,插值点按顺序随机选取,其他点用直线连接。点的坐标初值要以变量的形式定义,以便于分析时轴向横截面母线形状的变化,达到对变幅杆形状的优化。各点初始坐标定义见表2。

表2 模型初始点的坐标

在表 2中,点1、点 2为变幅杆大端两端点,是固定值;点7、点8为变幅杆小端两端点,纵坐标是固定值;L为变幅杆谐振长度,为设计变量,同时定义为变幅杆小端处两端点的横坐标,点2～点7为变幅杆母线上的6个插值点[2]。

模型采用Plane82单元,此单元是Plane42单元的高阶单元,采用3次插值函数,无附加位移函数项,可用于平面应力,平面应变和轴对称问题的分析,位于XY平面内,且轴对称分析时 Y轴为对称轴[3]。网格采用自由式方法划分,便于模型改变后网格的自动延伸。初始模型如图1所示。

1.2 变幅杆的模态分析和谐响应分析

模型建好后先对其进行模态分析,设置模态提取方法为Block lanczos法,指定模态提取的频率范围为10～20 kHz,待提取的模态个数为5,边界条件为模型两端自由,进行模态分析。

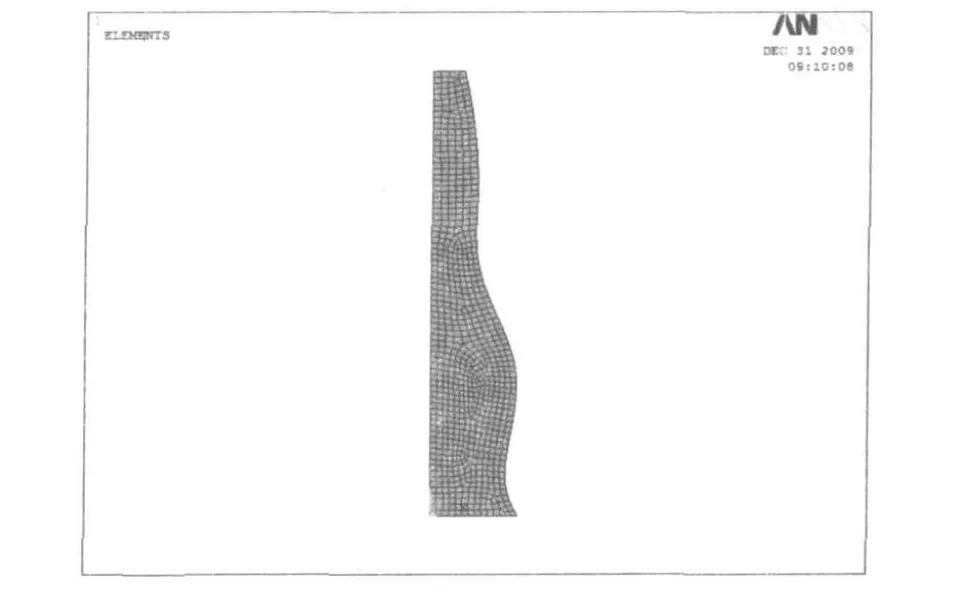
图1 6点插值样条变幅杆有限元初始模型

模态分析求解后,参数化提取初始模型的谐振频率f=14 697Hz。然后进行谐响应分析[4],采用Full法,在变幅杆大端所有节点上施加 Y方向频率为f=14 697 Hz,激振位移幅值为0.005 mm的按正弦变化的周期载荷,求解后参数化提取模型各端面产生的周期位移响应与应力分布。可获得模型大端输入振幅为 δ1=0.5×10-5m,小端输出振幅为δ2=-0.16×10-4m,从而可得到振幅放大比的倒数 F(X)=｜δ1｜/｜δ2｜,这里之所以得到放大比的倒数,是因为在下面的优化设计中要将它作为目标函数,而目标函数是要尽量小的数值。此外,还可得到模型的最大工作应力为 σ=54.7 MPa,并得如下公式[5]:

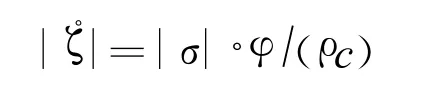
式中:ρc是变幅杆的特性力阻抗;ζ是变幅杆中的最大质点振动速度,σ是杆中的最大应力。

变幅杆中各质点振动是按正弦规律变化的简谐振动,其位移函数表达式为:

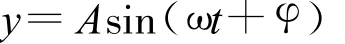
式中:A、φ、ω分别称为振幅、初相位、圆频率。

简谐振动的速度函数就是位移函数关于时间 t的一阶导,对上式求导数得:

2 变幅杆的优化过程和结果分析

2.1 变幅杆的优化过程

(5)指定零阶优化方法,零阶方法在ANSYS的优化设计模块中是最基本和常用的方法,可有效处理绝大多数工程问题。

(6)进行优化分析[6]。

2.2 变幅杆的优化结果分析

优化分析后可获得设计序列结果和后处理(图2),从而得到变幅杆最优形状与谐振长度(图3)。

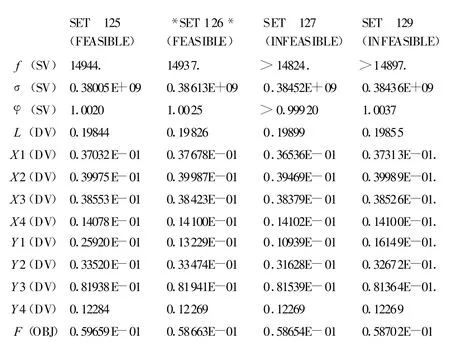
图2 优化设计数据

图3 优化设计图

由图2和图3可得到变幅杆的各性能参数:谐振长度为L=198.26mm;位移节点y位于离大端距离79.5 mm处;固有频率为14 937 Hz;形状因数φ=1.002 5;最大应力 σ=386.1 MPa;放大系数为MP=1/f=17。

然后将二维轴对称模型扩展成完整的三维模型,再对其进行模态分析得到固有频率为14 956 Hz,与二维轴对称模型结果基本相同;谐响应分析得到模型在频率14 956 Hz下的位移响应云图4和应力响应云图5。

图4 位移响应云图

图5 应力响应云图

由图4和5可看出,振幅放大系数、最大应力及形状因数等性能参数与二位模型优化分析结果基本相同,这也验证了用二维轴对称模型来代替轴对称实体模型进行有限元分析的正确性。

3 多点优化进行验证

以上是通过对变幅杆母线进行6点插值样条曲线进行的优化设计,为了验证其正确性,下面分别对9点插值和11点插值样条曲线进行优化。初始模型分别如图6、图7所示。

按之前的建模加载优化步骤进行优化后,得到的图形都与图2结果基本相同。由此可得到:当样条插值点逐渐增多时,优化后的变幅杆都将收敛于同一形状与谐振长度。

图6 9点插值样条变幅杆有限元初始模型

图7 11点插值样条变幅杆有限元初始模型

4 结论

基于传统形状变幅杆中阶梯型变幅杆放大系数较大但形状因数很小(一般都小于1),而圆锥形变幅杆形状因数较大放大系数却很小的原因,本文通过以3次样条曲线作为变幅杆轴截面的母线形状,采用二维轴对称建模的方式,在有限元动力学分析基础上利用优化设计的方法,优化出了一种既有较好形状因数又有很大放大系数的新型变幅杆,并通过9点插值、11点插值的形式对6点插值进行了验证,证明了此方法的正确性,为提高超声加工效率提供了一种新的思路与方法。

[1] 曹凤国.超声加工技术[M].北京:化学工业出版社,2005.

[2] 杨志斌.旋转超声加工装置的设计与新型变幅杆的研究[D].山西:太原理工大学,2008.

[3] 王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007.

[4] 赵莉,王时英,轧刚.超声加工中变幅杆的动力学分析[J].电加工与模具,2005(2):35-38.

[5] 林仲茂.超声变幅杆的原理和设计[M].北京:科学出版社,1987.

[6] 原丰霞,张慧君,朱国良.基于 ANSYS的超声变幅杆的优化设计[J].机械工程师,2004(11):24-26.