Delta算子不确定系统区域极点约束的H∞可靠控制＊

张洛花,田 巍,黄战峰

(河南城建学院,河南平顶山467036)

0 引言

可靠控制[1]是指在设计控制器时将系统部件(如执行器和传感器)可能发生故障的情形考虑在系统设计中,使得某些部件发生故障时系统仍能保持稳定。目前,关于可靠控制的研究已取得不少成果。王福忠等[2]根据修正的Lyapunov方程和LMI理论,研究了线性系统鲁棒区域稳定的可靠控制问题。文献[3]讨论了在区域极点和状态方差约束下动态系统的可靠控制问题。针对一类不确定线性系统,文献[4]研究了区域极点约束下的鲁棒可靠控制器的设计方法。但目前基于Delta算子系统可靠控制的研究还不多见。

基于传统的移位算子模型的可靠控制方法,在采样周期很小时将会引起病态条件问题。Delta算子[5]作为一种统一的模型描述形式,既避免了Z变换引起的数值不稳定问题,又使得传统的连续域设计方法可直接用于离散域设计,在系统控制和信号处理领域获得广泛应用。张端金等[6]研究了Delta算子不确定系统在多指标约束下的鲁棒H∞控制问题。文献[7]讨论了状态不确定Delta算子系统的D稳定鲁棒容错控制问题。肖民卿[8]在传感器故障为连续模型的基础上,研究了Delta算子系统D稳定可靠控制问题。

本文采用更一般的执行器连续故障模型,研究Delta算子不确定系统同时在区域极点和H∞范数界约束下的可靠控制问题。

1 问题描述

考虑Delta算子不确定线性系统

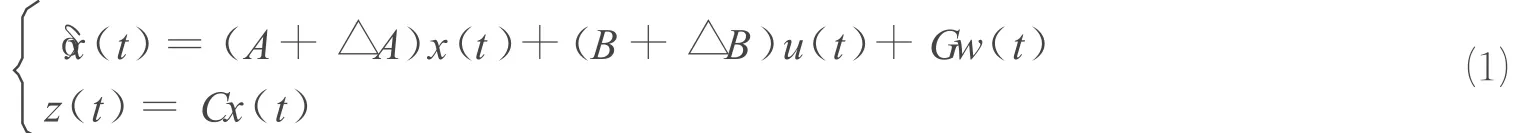
其中：δ即Delta算子,定义为δ=(q-1)/T,式中T为采样周期,q为前向移位算子;x(t)∈Rn为系统状态变量。u(t)∈Rm为控制变量;w(t)∈Rl为干扰信号;z(t)∈Rp为控制输出;A,B,G,C为适当维数的已知定常矩阵;△A,△B为系统不确定性,具有形式如下：[△A △B]=DF[E1E2],其中D,E1,E2为已知定常矩阵,表示系统不确定性的结构信息,F为满足FTF≤I的适当维数的不确定性参数矩阵,I为单位矩阵。

引入状态反馈u(t)=Kx(t),考虑到执行器可能失效的情况,引入表示执行器连续故障的矩阵M,并把其放在状态反馈增益矩阵K和输入矩阵B之间,其形式为M=diag(m1,m2,…,mp),其中：0≤mli≤mi≤mui。显然,当mi=0时,表示第i个执行器完全失效;当mi=1时,表示第i个执行器正常工作;当0≤mli≤mi≤mui且mi≠1时,第i个执行器部分失效;引入如下矩阵：

MO=diag(m01,m02,…,m0p),J=diag(j1,j2,…,jp),

L=diag(l1,l2,…,lp),|L|=diag(|l1|,|l2|,…,|lp|),

其中：

由此可知

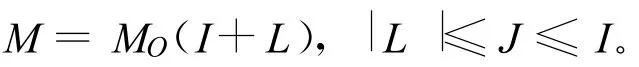
含执行器故障的Delta算子闭环系统可表示为

其中：Ac=A+BMK+DF(E1+E2MK)。

对于Delta算子系统,稳定性要求系统所有极点都在γ平面的圆形区域D(-1/T,1/T)内,即以(-1/T,0)为中心,1/T为半径的圆内。

为简便计算,引入记号

引理1[9]矩阵A的所有特征根位于圆盘D(a,r)内,当且仅当存在正定对称矩阵P满足

由引理1我们可推得如下定义：

定义1 Delta算子描述的故障闭环系统⑵状态反馈二次可D鲁棒容错镇定(即λ(Ac)⊂D(a,r)),当且仅当存在对称正定矩阵P满足

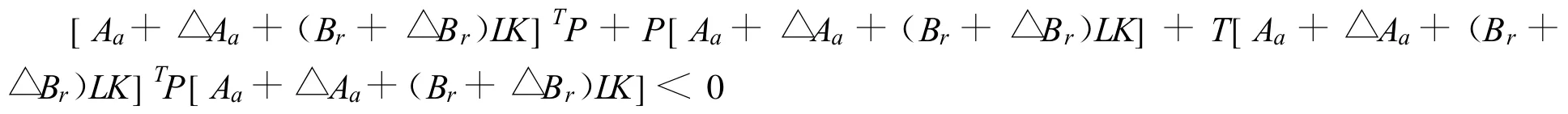
引理2[10]给定适当维数的矩阵X,F,Y,其中F是对称的,则F+XHY+YTHTXT＜0对所有满足HTH≤I矩阵H成立,当且仅当存在一个常数ε＞0使得F+ε XXT+ε-1YTY＜0。

引理3[6](Delta算子界实引理)考虑线性系统Twz(γ)的[C Abr]能检测实现

如果存在对称矩阵P≥0和实数γ1＞0使得

则Abr稳定且‖Twz(γ)‖∞=‖C(γ I-Abr)-1G‖∞≤γ1。

本文目的是：对于任意执行器失效情况M,求解状态反馈控制增益K,使得Delta算子系统(2)对所有容许的不确定性△A,△B,同时满足下列指标约束：

(a)对所有可能的连续故障M,Delta算子系统⑵的所有极点位于以(a,0)为圆心、r为半径的圆形区域D(a,r)内,即λ(Ac)⊂D(a,r)。

(b)从扰动输入w(t)到控制输出z(t)的传递函数Twz(γ)的H∞范数满足‖Twz(γ)‖∞=‖C(γ IAc)-1G‖∞＜γ1,其中：γ1＞0是一给定的常数.Twz(γ)的H∞范数定义为

‖Twz(γ)‖∞=式中,σmax(◦)表示矩阵最大奇异值,v∈L2定义为‖v(t)‖2=[S∞t=0v(t)Tv(t)dt]1/2＜∞,其中：S∞t表示连续情形的Riemann积分或离散情形的Riemann求和运算。

2 主要结果

定理1 考虑Delta算子不确定故障系统⑵,对于任意执行器失效情况M,存在状态反馈增益K,使得闭环系统满足条件(a)约束的充分条件是存在正定对称矩阵P及正实数ε1,使得下面矩阵不等式有解。

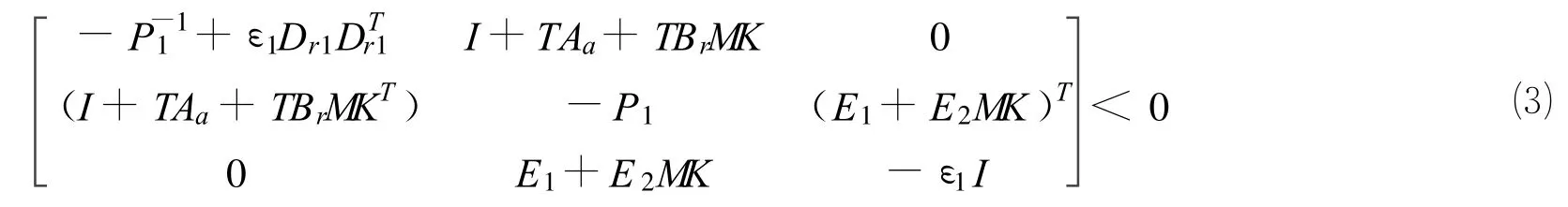
证明：由引理1和Schur补定理可知,Delta算子系统⑵满足区域极点配置(即λ(Ac)⊂D(a,r)),当且仅当存在对称正定矩阵P满足

其中：Acr=Aa+BrMK+DrF(E1+E2MK)。

将式⑷展开可得

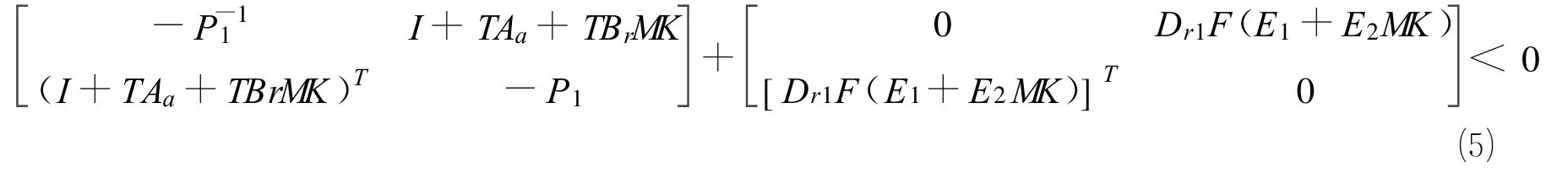
对式(5)进行分解,并令

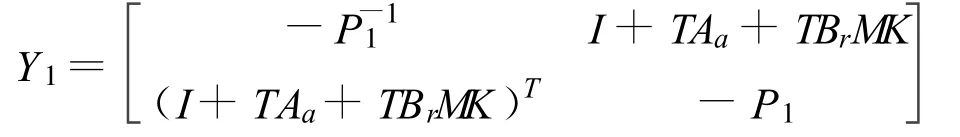
则式(5)等价于

因为FTF≤I,所以由引理2知式⑹成立,当且仅当存在一个实数ε1＞0使得

根据引理1可知上式等价于式⑶,定理1得证。

定理2 对于任意执行器失效情况M,存在状态反馈增益K使Delta算子不确定故障系统(2)稳定且满足‖Twz(γ)‖∞≤γ1约束的充分条件是存在正定对称矩阵P及正实数ε2,使得下面矩阵不等式组有解。

证明：由定义1和引理3可知,Delta算子系统(2)稳定且满足‖Twz(γ)‖∞≤γ1约束则需存在正定对称矩阵P1满足下面矩阵不等式

把式⑽展开可得

由引理2可知,式(11)等价于式(8)(具体推导过程与定理1类似),定理2得证。

定理3 对于任意执行器失效情况M,如果存在正定对称矩阵X,矩阵Y以及正实数ε1,ε2,ε3,ε4使得下面线性矩阵不等式组有可行解

则Delta算子不确定系统(2)同时满足约束条件(a)和(b)。状态反馈控制增益K=YX-1即为所要求的可靠控制律。其中：

证明：由定理1和定理2可知,要使Delta算子不确定系统(2)同时满足约束条件(a),(b),则需存在正定对称矩阵及正实数ε1,ε2,同时满足矩阵不等式(3)、(8)和(9)。由于定理1和定理2中的P、K是非线性的形式存在的,要直接从以上矩阵不等式中计算出P和K是非常困难的。因此,要通过变量替换的方法将非线性矩阵不等式化解为线性矩阵不等式来求解,并将故障模型化为连续故障模型的形式。

由于故障M为连续故障,即M=MO(I+L),我们将该式代入到式(3)可得

令

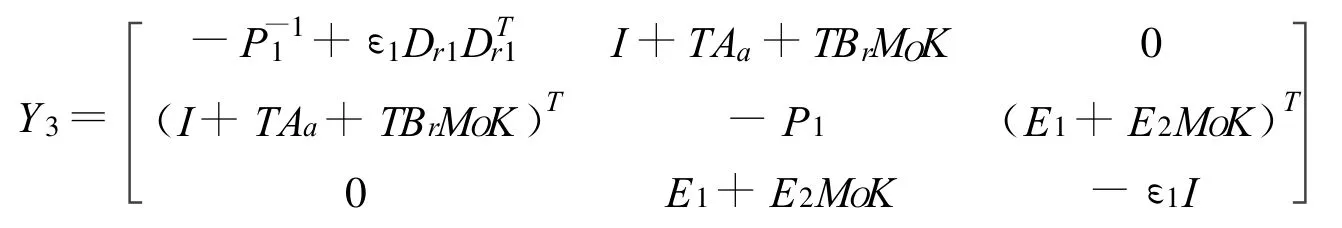
则式(15)等价于

又因为|L|≤J≤I,所以,由引理2知上式成立,当且仅当存在一个实数ε3＞0使得

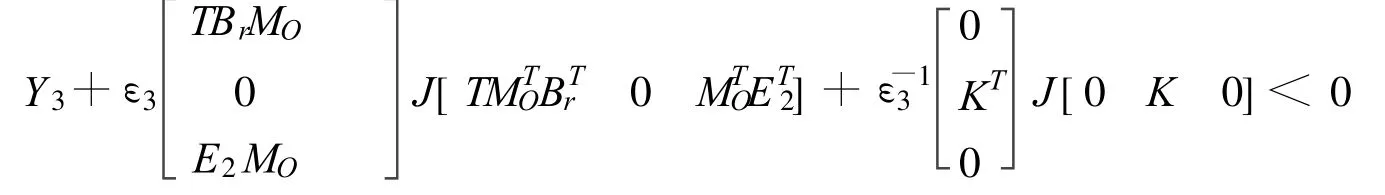
即

由Schur补定理可知,式⒄等价于

将式⒅分别左乘右乘diag(I,P-1,I,I)可得

同理,将式M=MO(I+L)代入式⑻可得

令

则式⒇等价于

又因为|L|≤J≤I,所以,由引理2知上式成立,当且仅当存在一个实数ε4＞0使得

先利用Schur补定理,再对式子分别左乘右乘diag(I,P-1,I,I,I)然后令X=P-1,Y=KX,N2=则式(22)可化简为式(14)。令X=P-1代入式(9),则式(9)等价于式(13)。

因此,若存在正定对称矩阵X和矩阵Y以及正实数ε1,ε2,ε3,ε4为关于变量(X,Y,ε1,ε2,ε3,ε4)的线性矩阵不等式组(12～14)的可行解,则由此求得的状态反馈控制增益K,不仅使得Delta算子系统(2)满足区域极点指标约束,而且满足H∞性能指标约束,即‖Twz(γ)‖∞≤γ1。

3 数值仿真

考虑Delta算子系统(2)的参数为：

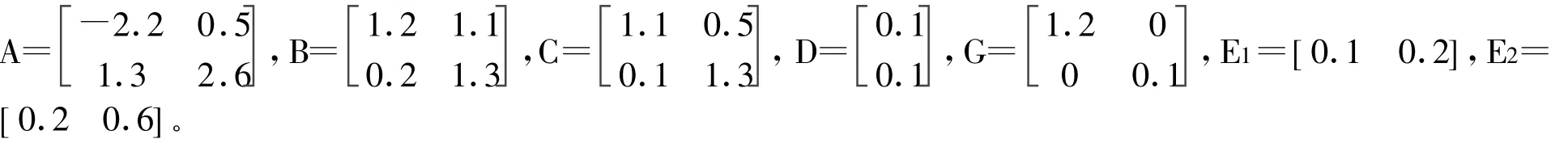
取圆形区域为D(a,r)=D(-15,15),采样周期T=0.05s。

通过直接计算可知

利用MATLAB-LMI工具箱中的求解器feasp,求解定理3中关于变量(X,Y,ε1,ε2,ε3,ε4)的线性矩阵不等式组(12～14),得其可行解为：

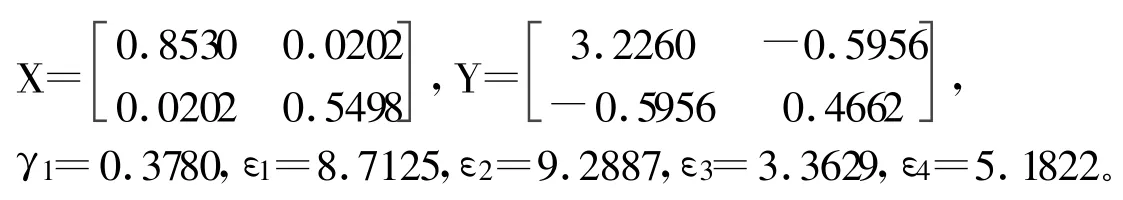
并由K=YX-1,可求得系统的状态反馈增益矩阵为：

由此可见,在执行器故障为连续故障模型下,通过求解定理3中的LMI组可以求得一个控制器,使得系统(2)保持稳定并且同时满足区域极点指标和H∞范数指标约束;由于是在更一般的故障模型下得到的,所以所得结果具有更小的保守性。

4 结论

本文基于连续故障模型,研究了一类Delta算子描述的不确定系统在区域极点约束下的H∞可靠控制问题。我们可以利用MATLAB-LMI工具箱得到同时满足圆形区域极点和H∞性能指标约束的鲁棒可靠控制器。由于采用的是更切合实际的连续故障模型,所得的结果不仅可以处理执行器完全失效时的情形,还可以处理其部分失效时的情形,从而降低了控制器设计的保守性。但定理3中可行解的存在性与所选取的性能指标有密切联系,需在可行范围内才有解,所以本文的结论还存在一定的局限性,有待进一步改进。

[1] Veillette R J,Medanic J V,PerkinsW R.Design of reliable control system[J].IEEE Trans on Automatic Control,1992,37(3)：770-784.

[2] 王福忠,姚波,张嗣瀛.线性系统区域稳定的可靠控制[J].控制理论与应用,2004,21(5)：835-839.

[3] 张刚,韩祥兰,王执铨.极点与状态方差约束下的动态输出反馈可靠控制[J].控制与决策,2007,22(3)：289-293.

[4] 费为银,丁德锐,夏登峰.不确定系统D稳定的鲁棒H∞可靠性控制[J].系统仿真学报,2007,19(8)：1772-1775.

[5] Middleton R H,Goodwin G C.Improved finite word length characteristics in digital control using delta operator[J].IEEE Trans.Automat.Contr.,1986,31(11)：1015-1021.

[6] 张端金,王忠勇,吴捷.Delta算子不确定系统的多目标鲁棒H∞控制[J].控制与决策,2003,18(2)：164-168.

[7] 刘满,井元伟,张嗣瀛.Delta算子系统D稳定鲁棒容错控制[J].东北大学学报：自然科学版,2004,25(8)：715-718.

[8] 肖民卿.传感器有故障的Delta算子线性不确定系统的鲁棒D稳定[J].控制理论与应用,2009,26(2)：183-185.

[9] 张端金,吴捷,杨成梧.Delta算子系统圆形区域极点配置的鲁棒性[J].控制与决策,2001,16(3)：337-340.

[10] Khargonekar P P,Petersen I R,Zhou K.Robust stabilization of uncertain linear systems：quadratic stabilizability and H∞control theory[J].IEEE Trans Automatic Control,1990,35(3)：356-361.