基于压缩传感理论的绝缘子泄漏电流数据压缩
2010-02-08黄建才朱永利
陈 青,黄建才,朱永利
(华北电力大学 控制与计算机工程学院,河北 保定 071003)
基于压缩传感理论的绝缘子泄漏电流数据压缩
陈 青,黄建才,朱永利
(华北电力大学 控制与计算机工程学院,河北 保定 071003)
绝缘子泄漏电流数据量大,给监测系统数据存储和传输带来巨大的负担。针对这个问题,提出基于压缩传感理论 (Compressed Sensing,CS)的数据压缩方法,CS将采样与压缩合并进行,少量采样就能很好地恢复信号,不仅降低对硬件要求,而且提高压缩效率。将泄漏电流信号进行小波变换的稀疏分解,然后对稀疏的泄漏电流信号进行高斯测量编码,最后应用正交匹配追踪算法 (O MP)重构信号。实验结果表明,对绝缘子泄漏电流进行CS数据压缩具很高的压缩比,恢复的信号也比较理想。
压缩传感理论;泄漏电流;小波变换;高斯观测矩阵;正交匹配
0 引 言
绝缘子污闪严重威胁电网安全运行,并给国民经济带来巨大的经济损失[1]。由于绝缘子表面污层受潮引发的污闪事故是不可避免的,所以及时准确地提供预警污闪的信息是十分重要的。
绝缘子泄漏电流包含丰富的污闪放电信息,能科学地表征绝缘子表面污秽程度,并且便于连续监测[1,2]。然而泄漏电流数据量庞大,增加了数据存储和传输代价。因此在保证尽可能完整提供原始泄漏电流信息条件下,如何降低泄漏电流数据存储和传输负担已成为重要的研究课题。
数据压缩技术对提高系统的数据传输和处理十分有效。然而绝缘子污闪时往往出现大量幅值不等且频率较高的电流脉冲群[2]。在传统采样中对传感器等硬件的采样频率要求很高;而压缩过程中还要丢弃这些大量高频采样的信息,存在计算和内存浪费等问题。
针对上述问题,本文提出基于压缩传感理论(CS)的绝缘子泄漏电流数据压缩。利用信号的稀疏特性,CS将采样复杂性转移到了重构计算复杂性,避免了直接对泄漏电流信号采样,给信号采集技术带来革命性突破[3,4]。将泄漏电流信号进行小波变换的稀疏分解,然后对稀疏的信号进行高斯测量投影,最后对压缩后的数据采用正交匹配追踪算法 (O MP)恢复。实验结果表明,该方法不仅提高了压缩比,而且重构效果也比较理想。
1 泄漏电流
污秽绝缘子泄漏电流是指在运行电压作用下,受污绝缘子表面受潮后测得流过绝缘子表面的电流[1,2]。它是气候条件 (大气压、温度、湿度等)、污秽和运行电压三个因素综合作用的结果,是动态参数。当运行电压不变时,泄漏电流最大值随绝缘子污秽度增加而增大;反之,当污秽度一定时,泄漏电流随运行电压的升高而增加[2]。
当绝缘子表面污秽积累到一定程度,在一定的外界环境下可能发生污闪放电现象。从运行中对污秽绝缘子的监视和预报角度看,可将污闪放电过程分为安全区 (A)、预报区 (B)、危险区(C)和闪络区 (D)4个阶段[5]。如图 1所示某段污闪泄漏电流时域波形图。
从图 1可以看出绝缘子泄漏电流波形特点:

图1 绝缘子污闪泄漏电流波形图Fig.1 Leakage current waveform of insulator flashover
(2)预报区中泄漏电流呈不稳定状态,常以脉冲群出现,电流幅值增大。
(3)危险区泄漏电流脉冲幅值迅速增加,高幅值脉冲密度增加。
(4)闪络的前半个周波的泄漏电流 (即临闪电流)最大。闪络区绝缘子泄漏电流的幅值变化快,频率高。
综上可知,绝缘子泄漏电流是一种非平稳,非线性的突变信号。虽然绝缘子泄漏电流是比较理想的动态参数来监测绝缘子污秽水平,但是采集系统面临巨大的数据存储和传输负担。如何高效率地压缩泄漏电流数据一直是我们非常关注的课题。
2 压缩传感理论
在压缩传感理论中,信号的采集和压缩同步进行,使传感器的采集和计算成本大大降低。将信号非自适应线性投影通过求解最优化问题重构原始信号。信号的投影测量数据量远远小于传统采样方法所获的数据量,突破了香农采样定理的瓶颈,大大降低了非平稳泄漏电流数据采集量[6,7]。
压缩传感理论主要包括信号的稀疏表示、观测矩阵设计和重构算法三个方面。
2.1 信号稀疏表示

式中:f和 x是 N×1矩阵;Ψ是 N×N矩阵。x是信号 f的等价表示,当 x仅有 K(K<<N)个非零元时,f是可压缩的,称 Ψ为信号 f的稀疏基。常用的稀疏变换基有:正 (余)弦变换基、快速傅里叶变换基、小波变换基等[6]。
2.2 观测矩阵

由于测量向量维数 M远远小于信号 x维数 N,求解式 (2)的逆问题是一个欠定方程。在保证算法的收敛性条件下,K个非零元能够由 M个测量值准确地恢复,ΦψT矩阵必须满足约束等距性 (RIP),且保证稀疏变换基Ψ和观测矩阵 Φ不相关[7]。
以实践教学为主线,根据“卓越计划”的“通用标准”参考“行业专业标准”[3],构建校企联合的“3+1”培养模式和有效机制[4]。
高斯随机矩阵满足 RIP条件,几乎与任何稀疏信号不相关[7],本文采用该测量矩阵实验。其常见的能满足约束等距性的测量矩阵有:局部傅里叶矩阵、局部哈达玛矩阵和二值随机投影矩阵等[7]。
2.3 信号重构
由 M个测量向量 y重构原始信号 f是一个求解最优化问题。常采用重构效果较好的正交匹配追踪算法 (O MP),其本质思想是:以贪婪迭代的方式选择 Φ的列,使得在每次迭代中选择的列与当前的冗余向量最大程度地相关,从测量向量中减去相关部分并反复迭代,直到迭代次数达到稀疏度K,强制迭代停止[8,9]。具体的算法步骤如下:

O MP重构过程中,迭代次数满足稀疏度 K,且测量数质量 M必须满足 M~O(K ln(N))时,才能精确地恢复信号,重构的计算复杂度为 O(NK2)[8,9]。由此可见,稀疏度与信号的重构精度和计算复杂度密切相关。
3 实验结果与分析
在盐度 (ESDD)为 0.4 mg/cm2、灰度 (NSDD)为 2 mg/cm2情况下,采样频率为 10 kHz下绝缘子表面泄漏电流。由于一次完整的绝缘子污闪过程所采集的泄漏电流数据量非常大,为了充分体现 CS对非平稳信号数据压缩的有效性,仅取临闪阶段的部分泄漏电流数据。具体实验步骤如下:
(1)选择小波基为稀疏变换基,根据式 (1)得到原始泄漏电流的信号稀疏表示。
(2)对稀疏的泄漏电流信号进行高斯投影测量,获得压缩后的数据。
(3)对压缩后的数据进行 O MP重构,得到恢复后的信号。
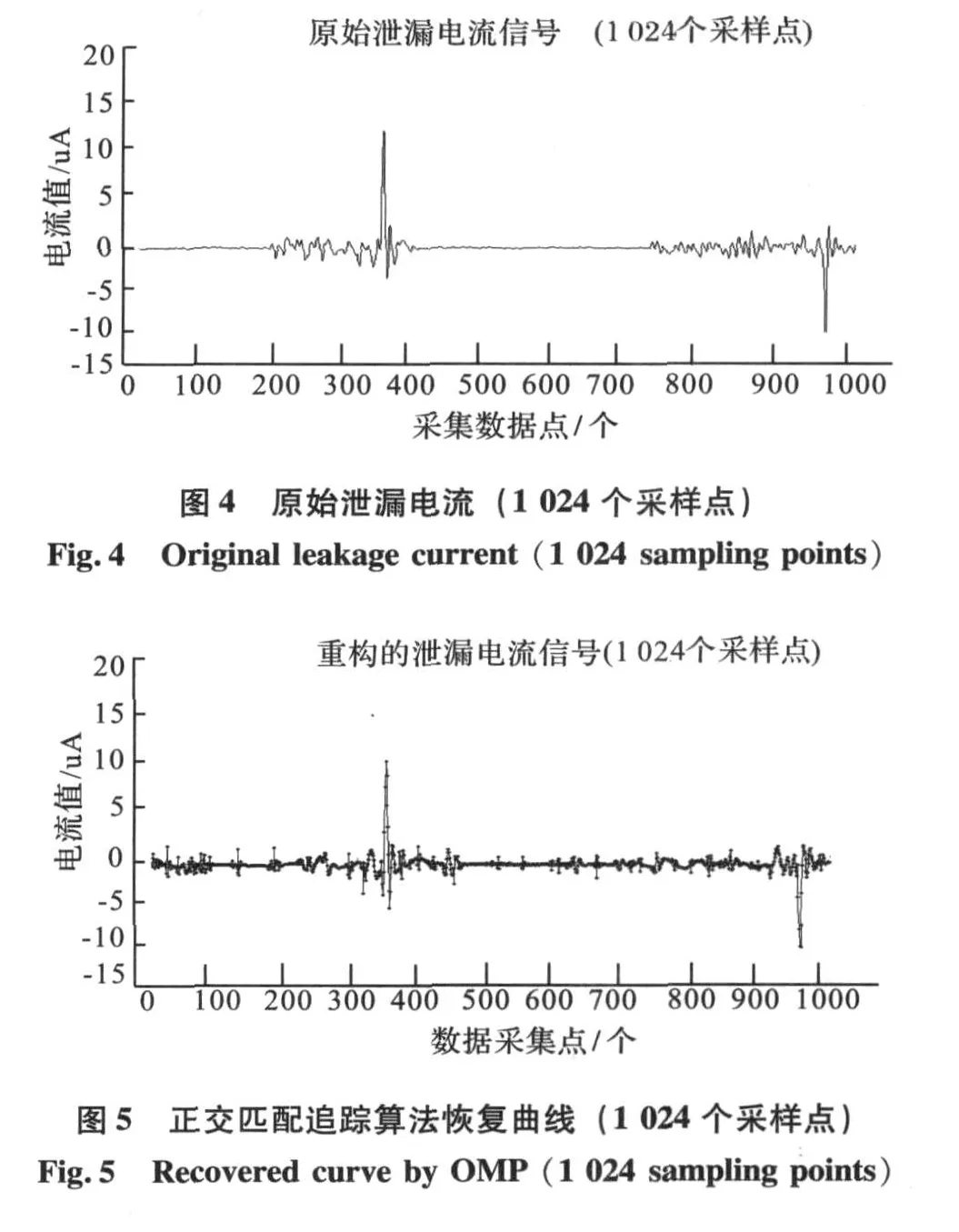
如图 2和图 4分别表示某段 512个和 1024个采样点的原始绝缘子泄漏电流图。从图 2,4可知,绝缘子污闪泄漏电流具有高频突变性,闪络时出现极大的脉冲电流。

对于恢复后的信号失真程度,通过以下的均方根来测量信号的重构误差[14]:
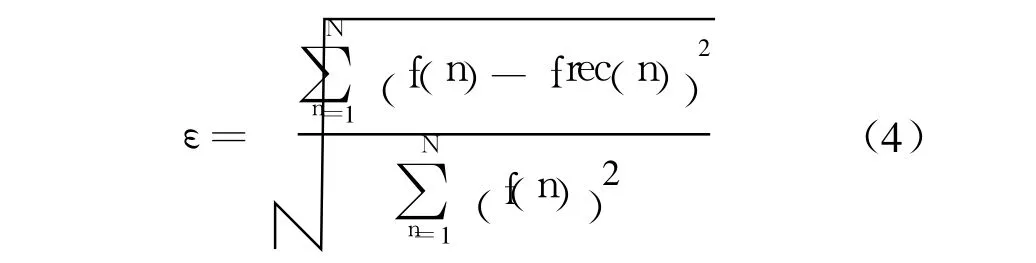
式中:f为原始数据;frec为重构数据;N为数据采集点的个数。
如图 3和图 5分别为对上述泄漏电流进行 CS压缩后应用 O MP恢复的信号图,实点为压缩后的数据点。对比原始泄漏电流信号图和恢复图像可见重构结果还是比较理想的,但低频信号部分数据恢复出现的偏差较大。依据式 (4)实验得出:512个采样点的压缩比为 12.3∶1,重构误差为0.765 9;1 024个采样点的压缩比为 14.2∶1,重构误差为 0.608 1。对比可知,数据量越大,重构误差越小,压缩比越高。
4 结 论
本文应用 CS方法可以保持原始泄漏电流信号的结构信息,使泄漏电流的存储和传输数据量大大减少。仍然存在一些问题需要研究。
(1)选择的小波变换基对泄漏电流的高频突变部分稀疏分解效果较好。但小波分解受小波基的种类和分解尺度因素的影响,对于非平稳的泄漏电流信号,同一小波基就难以满足不同频率段泄漏电流信号特征需要。
(2)高斯观测矩阵对稀疏的泄漏电流信号从高维投影到低维,以较少的测量值包含了足够的重构信息量。但测量矩阵是预先设计好的,不能根据信号自适应变换。
(3)O MP重构原始泄漏电流信号。重构误差和压缩比结果表明,CS理论具有较高的压缩比,而且数据量越大,压缩比越高,重构误差越小。然而重构算法的计算量比较大。
[1]关志成,毛颖科,王黎明.污秽绝缘子泄漏电流特性研究 [J].高电压技术,2008,34(1):2-6.
Gung Zhicheng, Mao Yingke,Wang Liming.Review on leakage current characteristics of contamination insu lators[J].High Voltage Engineering,2008,34(1):2-6.
[2]杜欣慧,戴云航,王志刚,等.饱和受潮条件下的绝缘子泄漏电流特性 [J].高电压技术,2007,33(9):6-9.
Du Xinhui,DaiYunhang,Wang Zhigang,etal.Characteristics of leakage current of insulators in saturated moisture condition[J].H igh Voltage Engineering,2007,33(9):6-9.
[3]石光明,刘丹华.压缩感知理论及其研究进展 [J].电子学报,2009,37(5):1070-1081.
Shi Guangming,Liu Danhua.Aduances in theory and application of compressed sensing[J].Acta Electronic Sinica,2009,37(5):1070-1081.
[4]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[5]梅冰笑.覆冰与污秽绝缘子闪络试验中泄漏电流测量系统研究 [D].重庆:重庆大学,2005.
MEIBingxiao.Realization and design of leakage current detectiong system of flashover process on iced insulators[D].Chongqing:Chongqing University,2005.
[6]Candès E,Romberg J.Sparsity and incoherence in compressive sampling[J].Inverse Problems,2007,23(3):969-985.
[7]Figueiredo MA T,Nowak R D,Wright S J.Gradient projection for sparse reconstruction:application to compressed sensing and other inverse problems[J].IEEE JSTSP,2007,1(4):586-598.
[8]方红,章权兵,韦穗.改进的后退型最优正交匹配追踪图像重构方法 [J].华南理工大学学报,2008,36(8):23-27.
Fang Hong,Zhang Quanbing,Wei Sui.Image reconstruction based on Improved backward optimized orthogonal matching pursuit algorithm[J].Journal of Suoth China University of Technology,2008,36(8):23-27.
[9]TroppJ,Gilbert A.Signal recovery from partial in formation viaorthogonalmatching pursuit[J].IEEE Trans on Inform Theory,2007,53(12):4566-4666.
Data Com pression of Insulator Leakage Cu rrent Based on the Compressed Sensing
Chen Qing,Huang Jiancai,Zhu Yong li
(Schoolof Controland Computer Engineering,North China Electric Power University,Baoding 071003,China)
The huge data of insulator leakage current increases the burden of data storage and transmission in the monitoring system.Aiming at this problem,the paper puts forward data compression based on the compressed sensing.Compressed Sensing(CS)combines sampling and compression with a small amount of sample to reconstruct signalwell,which noton ly reduces hardware requirements butalso improves compression efficiency.First leakage current was decomposed by Wavelet Transform.Then adopted Gaussian observation matrix to compress the sparse leakage current.Reconstructed signal by Orthogonalmatching pursuitalgorithm(O MP)finally.The experimental results show that insulator leakage currentwas processed by CS,which had high compression ratio and rather reconstruction signal.
compressed sensing;leakage current;wavelet transform;Gaussian observation matrix;orthogonal matching
T M855
A
2010-04-17。
国家自然科学基金资助项目 (60974125)。
陈青 (1985-),女,硕士研究生,研究领域为计算机测控技术、课题电力系统数据压缩,E-mail:Chenyang 5869@163.com。
