教育移动机器人路径规划技术研究
2010-01-29刘尧
刘 尧
(西安市长安区第二中学数学组,陕西西安 710100)
机器人课程已进入高中教育阶段,移动机器人作为机器人的一个重要分支具有典型的代表意义,它集合了机械、电子及人工智能等先进技术,是学生学习机器人技术、教学实验和锻炼动手能力理想平台[1-2]。目前,教育机器人比较普及,其教学对象大多针对大学学生,但高中学生基础知识比较缺乏,对目前的机器人学理论无法理解[3-6],因此本文针对这一现状,研究一种基于模糊控制的移动机器人路径规划技术,便于学生理解与实践。
1 障碍物环境模型的建立
1.1 环境地图的建立
机器人采用占栅格地图[7],环境模型的建立方法如下:建立x-y坐标系(如图1所示),机器人的起始点设为S,全局目标点设为G,都处于第一象限。S的坐标为 (x′,y′),G 的坐标为 (x,y)(x> x′> 0,y>y′>0)。根据x,y的值在第一象限内建立一个大小为x×y的二维矩阵D。矩阵中,值为 0的元素代表障碍物单元,值大于 0的代表自由单元,列向量对应x轴的正方向,行向量对应y轴的正方向。障碍物信息就包含在环境信息当中。
在此元素坐标系中,矩阵 D元素的下标(b,c)等于元素在坐标系中的坐标(x,y),矩阵元素值z在坐标系中表示成函数
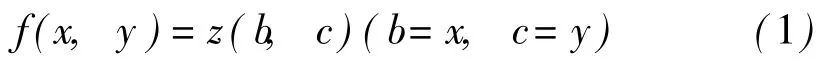
这样就可以根据函数判断点(x,y)是自由元素还是障碍物元素。
坐标系中,机器人的实时位置设为P(x,y)。机器人的路径规划在这个环境模型中,就是计算出一条代表自由单元矩阵元素的曲线,即一维向量x和y。

图1 在环境模型矩阵上建立坐标系
1.2 障碍物模型的描述
在路径规划仿真时,假设障碍物已事先根据机器人的实际尺寸和安全性要求进行了“膨化”,使得处理后的障碍物边界以外为安全区域。机器人将简化为一个质点。机器人无全局信息,它只能根据超声传感器感知的环境信息推算当前视线内的临时目标T。
1.2.1 障碍物识别
超声波传感器的配置方案和安装角度如图2,把3个超声传感器分为 S1、S2和 S3。对于单个的传感器来说,只能获得障碍物的距离信息,并不能得到障碍物的准确方位信息,导航误差增大。为此,提出一种简单明了的分区算法,对每个方向组的传感器测得的数据进行融合,从而得到 3个方向上障碍物距离和方位信息。,超声传感器最大测距范围为 5 m,当障碍物在 5 m之外时传感器距离值为 5m。

图2 障碍物传感器信息示意图
假定:3个传感器距离信息值用 di(i=1~3)表示,融合后取值(d,θ),d表示距离值,d的取值范围为(55 cm,500 cm),三个方向上分别为 dr、df和dl,θ表示障碍物方位角度,当有多个障碍物时,取使值最小的 θ值
另外,当障碍物在左方与前方共有区域,认为障碍物是在左方,当障碍物在右方与前方共有区域,认为障碍物是在右方。至此,得到了探测机器人前方 3个方向上障碍物距离信息的三维向量D1{dr,df,dl},传感器信息分区可以顺利地完成传感器信息初步融合,从而可以建立移动机器人障碍物环境模型。
根据向量D1{dr,df,dl}取值来设定探测机器人车体周围环境的类别,每个方向上有障碍物时该方向分量取值为 1,无障碍物取值为 0,则三位二进制代码即可对环境进行分类,共有 8种类。具体定义如下:
000:无障碍物,为了简化神经网络输出,定义为第 0类,记为 EN0;
001:左方有障碍物,定义其为第 1类,记为EN1;
010:前方有障碍物,定义其为第 2类,记为EN2;
011:前方和左方有障碍物,定义其为第 3类,记为EN3;
100:右方有障碍物,定义其为第 4类,记为EN4;
101:左方和右方有障碍物,定义其为第 5类,记为EN5;
110:前方和右方有障碍物,定义其为第 6类,记为EN6;
111:三个方向都有障碍物,定义其为第 7类,记为 EN7。
2 路径规划的模糊算法
得到环境分类信息后,我们采用模糊控制器来实现局部路径规划信息融合的最后一步。为满足系统要求,选用三维控制器进行控制。实现模糊控制步骤如下。
2.1 确定结构
该控制器共有 3个输入:环境类别、当前机器人速度 V和当前障碍物方位角度信息 θ;经过模糊逻辑处理后输出两个变量:机器人的速度 V和转角 φ。
2.2 确定语言变量值及其隶属函数
环境类别为 0~7共 8个离散值;当前机器人速度V模糊化取值语言变量为{快,中,慢},隶属函数取梯形函数,见图3;输出速度Vo模糊化与输入速度值相同;输出转角取值为 3个离散值: φ,0,- φ,(φ=5°)。

图3 当前机器人速度V及输出速度Vo隶属函数
2.3 模糊规则的建立
由以上变量取值得知可以制定共 72条模糊规则。参考Mamdani控制规则制定的方法取舍之后,制定了如下 24条 IF-THEN形式的模糊规则。
(1)当环境类别 EN为 0时,不考虑 θ:
1)若 V为快和中,输出Vo保持不变, φ为 0;
2)若 V为慢,输出 Vo为快, 为 0。
(2)当 EN为 1时:
3)若 V为慢,则输出 Vo为中, φ为 0;
4)若V为快,则输出 Vo为快, φ为 0;
(3)当 EN为 2时:
5)若V为慢, 则输出 Vo为慢, φ为-φ;
6)若V为快, 则输出 Vo为中, φ为-φ;
7)若V为中, 则输出 Vo为中, φ为-φ;
(4)当 EN为 3时:
8)若V为快,则输出Vo为中,为;
9)若V为慢,则输出Vo为慢,为;
10)若V为中,则输出Vo为中,为;
(5)当 EN为 4时:
11)若为左方,V为慢,则输出Vo为快, φ为 0;
12)若为左方,V为快,则输出Vo为快, φ为 0;
(6)当 EN为 5时:
13)若 V为快,则输出 Vo为中, φ为 0;
14)若 V为慢,则输出 Vo为中, φ为 0;
15)若 V为中,则输出 Vo为中, φ为 0;
16)若 V为退,则输出 Vo为慢, φ为-φ;
(7)当 EN为 6时:
17)若 V为快,则输出 Vo为中, φ为-φ;
18)若 V为慢,则输出 Vo为慢, φ为-φ;
19)若 V为中,则输出 Vo为中, φ为-φ;
(8)当 EN为 7时:
20)若 V为快,则输出 Vo为退, φ为 0;
21)若 V为中,则输出 Vo为退, φ为 0;
22)若 V为慢,则输出 Vo为退, φ为-φ;
23)若 V为退,则输出 Vo为退, φ为-φ;
(9)若当前情况不属于上述 8种情况,则保持当前状态不变。
2.4 控制输出的非模糊化
模糊推理结果都是模糊值,不能直接用于控制被控对象,需转换为执行机构可以执行的精确量。将模糊量转换为精确量的过程就叫非模糊化,方法有:最大隶属度法、中位数法、加权平均法等。其中应用最多的是加权平均法,可用式(2)计算。
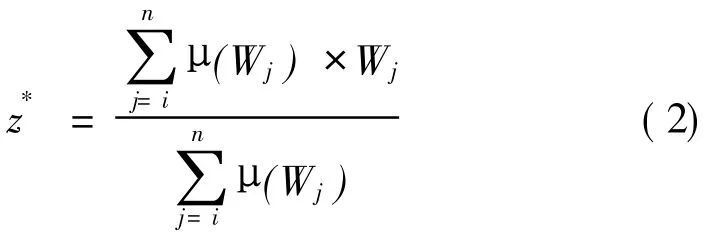
其中,Wj为推理结果,即经模糊规则判断后的输出,μ(Wj)为各种推理结果的权函数,为方便起见,可以取隶属函数为全函数。在这里Wj为输出速度Vo,而输出转角 φ本身即为精确值。
由此可以得到简单有效的移动机器人路径规划算法。
3 仿真与试验
基于以上方法在Matlab7.0上进行仿真试验。机器人在复杂的环境中能够快速顺利地规划出一条无碰撞的较优路径。
在一幅RGB格式的图片中建立黑白的环境信息,黑色区域表示障碍物,白色的表示机器人可以通过的区域。RGB图像由一个表示色素值的三维矩阵构成[8],建立的环境信息是黑白的,故三维矩阵的 3个二维矩阵是完全相等的,取出其中的一个二维矩阵。在这个矩阵的基础上按上述方法建立坐标系,同时显示出原图片,在这个图片上画出规划出来的路径[9],如图4所示。

图4 规划路径
图4(a)是在复杂环境中机器人对环境做出的局部路径规划结果;图4(b)是在仿真实验室环境中,对给定环境和目标,机器人做出的全局路径规划结果
对移动机器人实验平台在实验室环境中做了五次实际路径规划测试,并与仿真规划路径理论结果比较,可以得到机器人控制系统的综合性能水平,其定位误差比较如下:可以看出,机器人的控制性能是比较令人满意的,最大控制误差是 80 mm。但也存在随运行路径的延续,积累误差增大的问题,这主要是由以下原因引起的:
(1)机器人定位算法存在定位误差。
(2)机器人电机控制系统存在控制误差。
(3)机器人机械结构存在机械性误差。
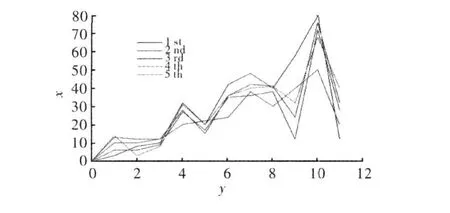
图5 实际路径规划实验误差
要解决这一问题,应在已知关键位置对机器人定位误差进行修正,使之不再积累。
5 结束语
本文针对高中机器人教育现状,研究设计了一套实用移动的机器人局部路径规划方法,实验证明,该方法切实有效,切对于高中学生比较容易理解,会促进学生的实践能力,激发学生学习机器人的兴趣。
[1] 王吉岱,李维赞,孙爱芹等.教育机器人的研制与发展综述[J].现代制造技术与装备, 2007,2(177): 10-12.
[2] 张传才,贺利乐,匡伟春.轮式移动教育机器人避障方法的研究[J].现代电子技术,2007,13(252):116-117.
[3] 江桦.基于嵌入式移动机器人的模糊控制算法设计[J].自动化与仪表, 2010(3):33-36.
[4] Borenstein J,Koren Y.The Vector Field Histogram-fast Obstacle Avoidance for Mobile Robots[C]. IEEE Trans.Robotics and Automation.,1991, 7(3): 278-288.
[5] Jing X, Zbigniew M,Lixin Z, et al. Adaptive Evolutionary Planner/navigator for Mobile Robots[C].IEEE Trans.Evolutionary Computation, 1997,1(1): 18-28.
[6] 张纯钢,席裕庚.全局环境未知时基于滚动窗口的机器人路径规划[J].中国科学:E辑,2001,1(31):51-58.
[7] 魏宁,刘一松.基于栅格模型的移动机器人全局路径规划研究[J].机器人技术,2008,4(24):229-231.
[8] 董霖.Matlab使用详解[M].北京:科学出版社,2008.
[9] 肖潇,方勇纯,贺锋,等.未知环境下移动机器人自主搜索技术研究[J].机器人,2007,3(29):224-229.
