铁路桥限高防护架与超高车辆的碰撞分析
2010-01-29王金田曲淑英侯兴民鞠翱天
王金田,曲淑英,侯兴民,鞠翱天
(烟台大学土木工程学院,山东烟台 264005)
近年来,随着我国铁路事业的迅速发展,铁路桥梁大量兴建。截至2005年,我国共有42 300多座铁路桥梁,大部分是公路下穿的桥梁和涵洞。同时,公路运输的快速发展使得机动车辆迅猛增加,特别是大型自卸车、集装箱汽车以及特殊用途车日益增多,机动车辆撞击铁路桥的事故时有发生,给铁路桥梁及生命财产造成了巨大的损失。铁路桥梁的安全成为人们日益关注的一个问题。为此,国务院下发了新的《铁路运输安全保护条例》中规定:下穿铁路桥梁、涵洞的道路,应当按照国家有关标准设置车辆通过限高标志及限高防护架,机动车通过下穿铁路桥梁、涵洞的道路时,应当遵守限高、限宽规定,不得冲击限高防护架[1]。目前,我国的限高防护架损坏严重,且相关领域研究较少。因此,有必要对限高防护架的碰撞过程作深入分析,以提高防护架的抗碰撞能力,保护铁路桥梁的安全。
本文以一防护架受汽车碰撞过程为例,基于ANSYS/LS-DYNA对其碰撞过程进行了分析,并获得了碰撞过程中防护架的变形、应力、荷载、能量转换的一般规律和特点,从而为同类防护架结构的设计、维护和损伤评估提供理论上的支持。
1 显式有限元动力分析模型
铁路桥限高防护架与机动车辆的碰撞过程是一个瞬态的复杂的物理过程,它包含以材料的非线性应力应变关系为特征的材料非线性和以结构的大位移、大变形为特征的几何非线性,这些非线性物理过程的综合作用使得防护架的碰撞求解变得十分困难,故此类问题常采用数值解。
碰撞问题的运动方程一般可以表示为
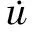
(1)
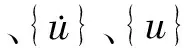
上述碰撞问题一般用时域内的显式中心差分方法进行动力反应数值计算。该方法不需要进行矩阵分解或求逆,不需要求解联立方程组,计算速度快,通过自动控制计算时间的步长,可以得到保证精度的稳定解。
2 防护架和汽车碰撞的有限元模型
基于ANSYS/LS-DYNA软件,在下列假定的基础上建立了汽车碰撞防护架的有限元模型。
2.1 基本假定
(1)将汽车模型简化为一个等质量、等尺寸的厢式模型。
(2)防护架底端与基础采用固结的方式连接,暂不考虑基础与防护架的相互作用。
(3)碰撞角度为90°。
(4)将车厢底部节点z方向(竖向)的位移自由度进行约束,防止在碰撞过程中车厢在竖直方向产生位移。
2.2 材料模型
由于限高防护架和汽车的碰撞是一个瞬态过程,材料的损伤具有一定的速率,因此本文选用与应变率相关的随动塑性材料模型[2]。材料密度ρ=7.8×103kg·m-3,弹性模量E=2.0×1011N·m-2,切线模量Etan=7.63×108N·m-2,初始屈服应力σ0=3.1×108N·m-2,泊松比υ=0.27。应变率用Cowper-Symonds模型来考虑,用与应变率有关的参数表示屈服应力,如式(2)所示
(2)

2.3 有限元模型
(1)防护架的有限元模型
限高防护架基础以上部分为热轧无缝钢管焊接而成。模型所用单元为solid164。假定各部分构件的尺寸如下:立柱高4.74 m,截面为φ280 mm×10 mm;立柱间支撑长1.0 m,截面尺寸为φ180 mm×10 mm;横杆长9.0 m,截面尺寸为φ180 mm×10 mm,横杆间支撑长1.0 m,截面尺寸为φ110 mm×5 mm。
(2)车厢有限元模型
参考我国陆路运输集装箱的几何尺寸,车厢模型尺寸取为6.0 m×2.5 m×2.5 m,底板厚50 mm,其余板厚10 mm,所用材料模型和单元类型与防护架一致。
碰撞有限元模型如图1所示。网格划分过程中上部横杆和支撑的网格尺寸定义为30 mm,两侧立柱和支撑的网格尺寸定义为60 mm,车厢前部碰撞区域网格尺寸为30 mm,其余部分为60 mm,原因在于碰撞区域应力较大,故网格划分较为精细。车厢与横杆的接触采用单面接触算法。
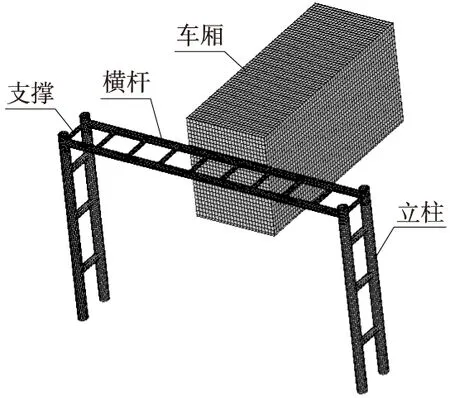
图1 整体有限元模型
3 计算结果及其分析
以碰撞初速度4、7、10 m/s 3种工况为例,讨论铁路桥限高防护架被撞击后的破坏情况。本文所讨论的防护架碰撞问题属于空间三维受力问题,因碰撞方向沿x轴方向,防护架在x轴方向的动力响应比其他两个方向的动力响应要大的多,所以本文以碰撞方向的动力响应为例讨论防护架的碰撞过程。
3.1 不同工况下防护架的应力及变形情况
3种工况下,限高防护架的整体变形及应力如图2所示,从图中可知:防护架结构的损伤变形一般出现在横杆中间的碰撞区域、横杆间的支撑区域以及上部节点区域。
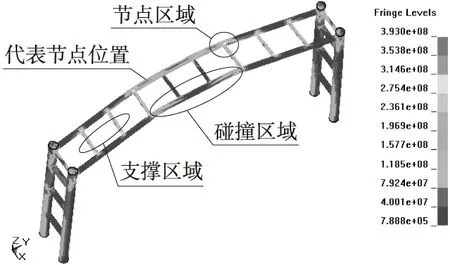
图2 防护架变形及应力
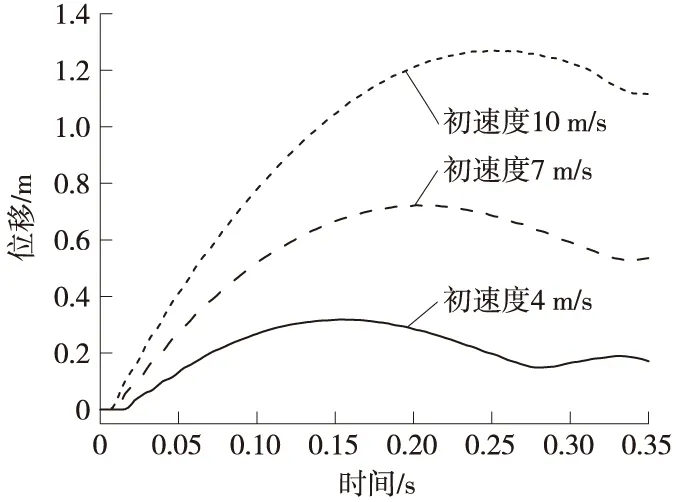
图3 不同工况下节点位移时程曲线
从碰撞区域内取一代表节点,其在3种工况下的位移时程曲线如图3所示,由图可知3条曲线总体趋势大体一致,位移都是由零达到最大值,然后由最大值逐渐减小,最后趋于稳定。最大值代表节点的最大位移,最后的稳定值代表节点的最终位移。由图可知:随着初始碰撞速度的增大,位移达到最大值和稳定值所用的时间越来越长,节点的最终位移越来越大。由此可以得到:随着初始碰撞速度的增大,碰撞作用时间越长,节点位移最终越大,防护架的破坏越严重。
下面以工况2(初速度为7 m/s)为例,说明限高防护架的各种变形,如图4、图5所示。整个碰撞过程中,防护架横杆与车厢接触的部位发生了严重的拉伸变形,且在接触区域的两端,横杆有明显的凹陷变形,0.21 s时变形达到最大,碰撞结束时,弹性变形恢复,只剩下不可恢复的塑性变形,如图4、图5中,t=0.32 s所示。横杆中间部位的变形是由车厢和横杆的接触作用造成的,损伤变形带有明显的局部性。支撑产生的主要是挤压变形,且支撑的中间部位应力较小,两端节点处应力较大,部分区域已经进入屈服状态,两端受力状态相似,都是一侧受拉,另一侧受压。

图4 不同时刻横杆碰撞区域变形
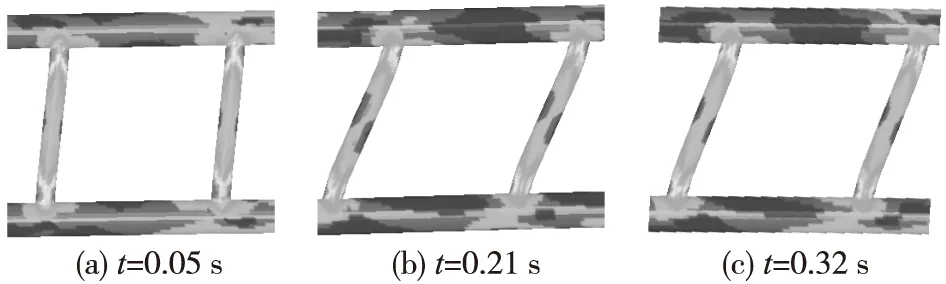
图5 不同时刻支撑与节点变形
3.2 碰撞力及其影响因素分析
撞击荷载是限高防护架结构设计的一个重要参数,同时撞击荷载时程曲线能够反映碰撞过程中防护架的损伤程度,以及损伤过程的变化情况,因此有必要对其进行讨论分析。图6是3种工况下的碰撞力时程曲线比较。
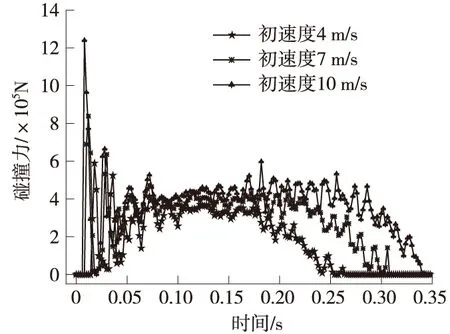
图6 碰撞力时程曲线
碰撞过程中,影响碰撞力的因素可能有以下几个方面:车辆的质量、速度;防护架的质量、结构形式、材料[4]。本文只讨论初始速度对碰撞力的影响。由图6可知,碰撞力时程曲线呈现出了非常明显的非线性波动特征:车厢和防护架接触以后碰撞力瞬间达到最大值,然后碰撞力逐渐减小并趋于稳定,最后随着车厢的反弹碰撞力逐渐减为零。分析原因如下:碰撞开始时,防护架处于弹性范围内,能量损失很少,致使碰撞力瞬间达到最大值,当防护架发生塑性破坏后,大量的能量转化为塑性变形能,碰撞力也随之减小,并逐渐至零。同时还可以看出:随着碰撞初速度的增大,碰撞荷载的最大值也相应增大,两者近似呈现正比例关系,稳定时的碰撞力相差不大。这说明碰撞初速度对碰撞荷载的影响较大,在设计中应着重考虑。
3.3 防护架的速度响应
由于碰撞过程中存在着一些复杂的非线性状态,所以传统的刚体碰撞求解方法在此已经不适用,数值模拟可以较为精确的解决此类问题。图7为工况2(初速度7 m/s)下,防护架不同区域中各取一代表节点的速度比较,图8为同一代表节点(图2所示)在3种工况下的速度比较。通过图7可知:与车厢接触区域的节点速度响应峰值最大,几乎是车厢初始速度的2倍;接触区域两侧的横杆节点速度响应峰值略小,与车厢的初始速度相当;远离碰撞区域的立柱节点速度响应峰值最小。同时由图8可以看出:随着碰撞初速度的增大,同一点的速度响应也随着增大。

图7 工况2节点速度时程曲线
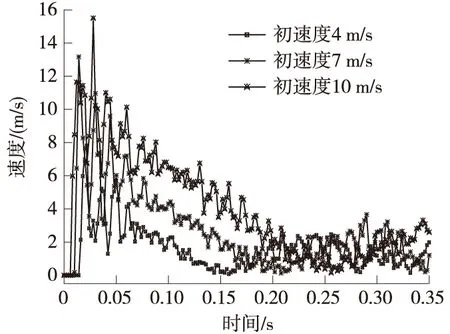
图8 节点速度时程曲线
由此可以发现碰撞过程中防护架的动力响应有以下特征:防护架中非碰撞区域的运动相比碰撞区域的运动有明显的滞后性。具体表现为与车厢接触的防护架碰撞区域运动状态最为激烈,碰撞接触区域附近的运动状态较碰撞区域运动有所减弱,远离碰撞区域的运动状态最弱。
3.4 能量变化
(1)系统能量变化

(2)防护架的能量变化
图10为防护架的总能量时程曲线,图11为防护架的动能时程曲线,由图10、图11可知:在0~0.21 s时间段内,防护架的内能呈增加趋势,动能相对于内能而言较小,并呈现逐渐减小的趋势。在0.21~0.32 s时间段内,防护架的内能有所减小,动能略有增加,原因在于弹性势能释放转化成车厢和防护架的动能。0.32 s以后,防护架中的弹性势能和动能交替转化。

图9 系统能量时程曲线
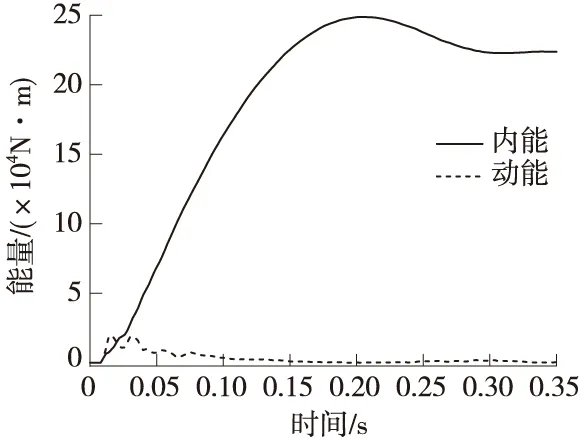
图10 防护架能量时程曲线

图11 防护架动能时程曲线
由以上能量变化分析可知,碰撞过程中系统能量大部分被防护架所吸收,转化为塑性变形能,说明防护架破坏严重,其抗碰撞能力有待提高。
4 结论
基于ANSYS/LS-DYNA对汽车和防护架的碰撞过程进行了数值模拟,得到了以下主要结论:
(1)碰撞过程中,防护架结构的破坏主要集中在上部横杆和支撑区域。碰撞初速度越大,碰撞作用时间越长,破坏越严重。
(2)碰撞过程中,防护架的动力响应表现出明显的区域性,即离碰撞区域越近,质点获得速度越大,运动越激烈。在防护架中体现为:从横杆中间部位到立柱的底端,各构件的动力响应依次减弱。
(3)碰撞力表现出明显的非线性特征,初速度对碰撞力影响较大。初速度与碰撞力最大值近似呈现正比例关系,这一关系可为设计中碰撞荷载的取值提供参考。
(4)防护架在碰撞中获得的动能与内能相比非常小,系统的能量绝大部分转化为结构的塑性变形能。
(5)在防护架结构设计中应加强上部结构构造,可在横杆间增加斜向支撑,同时也可适当增加横杆的壁厚,以提高上部结构的防撞击能力。
下一步的主要工作是考虑防护架与基础之间的动力相互作用,以提高仿真的精确度,并对不同结构形式的防护架进行碰撞分析。
[1]中华人民共和国国务院令第430号,铁路运输安全保护条例[S].
[2]廖其红,黄宏成,薛 量.薄壁钢结构碰撞性能仿真中材料模型研究[J].机械设计与研究,2001,17(4):64-66.
[3]石红星,白书锋,吕伟民.车与混凝土护栏碰撞的冲击力简化模型[J].公路交通科技,2002(2):10-12.
[4]陆新征,张炎圣,叶列平,等.超高车辆-桥梁上部结构碰撞的破坏模式与荷载计算[J].中国公路学报,2009,22(5):61-66.
[5]王 翔,刘又文,沈 庆,等.冲击载荷作用下钢筋混凝土结构动力响应仿真[J].力学与实践,2005,27(6):49-53.
[6]剧锦三,杨蔚彪,蒋秀根.刚体撞击弹塑性直杆时冲击荷载之数值解[J].工程力学,2007,24(6):49-53.
[7]刘晶波,杜修力.结构动力学[M].北京:机械工业出版社,2005.
[8]江德增,黄小清,汤立群.冲击荷载下半刚性护栏的非线性有限元分析[J].华南理工大学学报,2003,31(3):64-67.
[9]张文明,王 涛,张华兵,等.基于ANSYS/LS-DYNA的船桥碰撞分析[J].中国水运,2006,6(11):21-23.
[10]赖 跃.重型车辆与半刚性护栏碰撞的有限元分析[D].上海:同济大学,2006.
