一类线性约束下非光滑非线性规划问题的优化研究

张 鹏

(武汉科技大学管理学院,湖北武汉,430081)

关于线性约束下的非线性规划问题有过很多的研究。Zangw ill提出了次优化方法,其原理是将规划问题转化为一系列含等式约束的子问题,通过寻找最优解所在的流形使用无约束规划的方法求解原问题[1];Spedicato等运用ABS算法分别求解含线性等式约束和含线性不等式约束的非线性规划问题[2];Linderoth运用DC函数和双线性函数的线性下界函数提出求解非凸二次约束的非凸规划问题的分支定界算法[3];Vandenbussche等运用分支定界法求解具有箱形约束的非凸二次规划问题[4];Li提出分解算法求解大规模二次规划问题[5];Achache扩展了内点算法,提出了原始对偶路径依赖法求解凸二次规划问题[6];王永丽等提出滤子内点算法求解正定二次规划问题[7];高岳林等提出了求解凹二次规划问题的一个融合割平面方法的分支定界混合算法,并证明了算法是收敛的[8];赵敏等采用序列二次规划方法,将非线性规划转化为一系列二次子规划求解,并用信赖域二次规划的方法求解子规划问题,一定程度上降低了算法的复杂程度[9];夏少刚等提出了一种新的简易算法求解具有箱形约束的二次规划问题,并讨论了算法的有限步收敛性[10];张鹏等结合序列二次规划法和不等式组的旋转算法求解线性约束连续可微的凸规划问题[11-12]。上述问题的目标函数均是光滑的。

本文提出了一类线性约束下非光滑非线性规划问题,采用分块法和不等式组的旋转算法对该问题进行求解,同时还证明该算法的收敛性和有效性。

1 线性约束下连续不可微的非线性规划模型

1.1 模型描述

设非光滑的非线性规划模型为

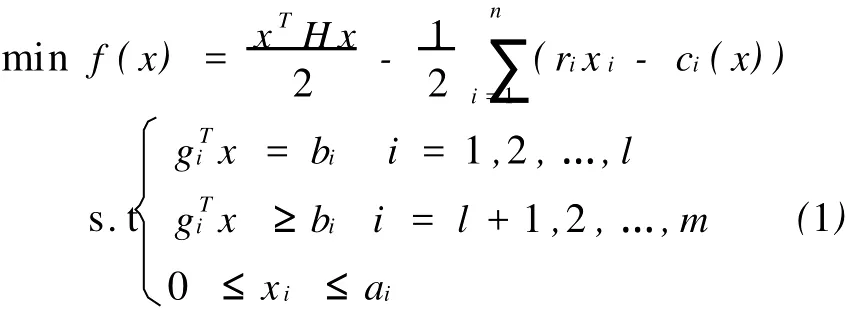
式中:H为正定或半正定矩阵;gi=(gi1,…,gin),i=1,…,n;f(x)为非光滑的非线性函数,其决策变量的交叉项为二次,非交叉项由线性函数和凹函数构成。ci(xi)为非光滑的凹函数,如图1所示。

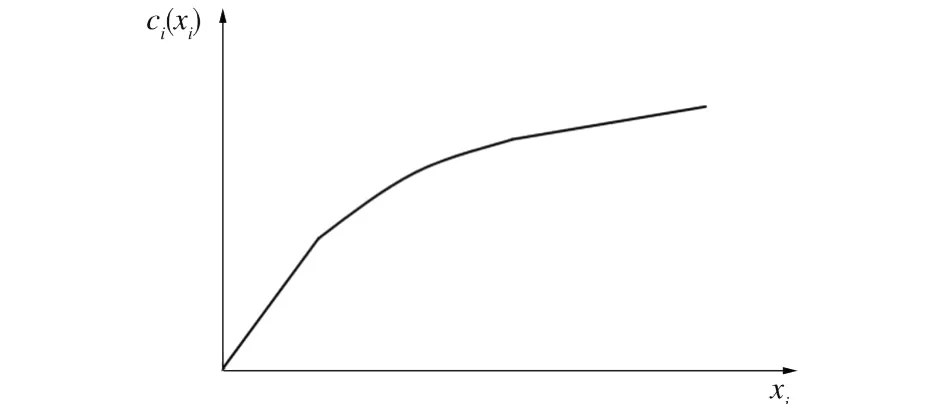
图1 非光滑凹函数Fig.1 Nonsmooth concave function

1.2 模型分析

ci(xi)为非光滑的凹函数,可用线性函数加以拟合,如图2所示。

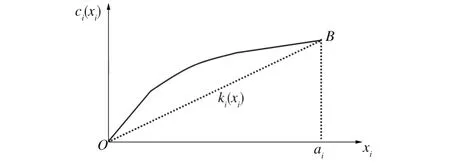
图2 非光滑凹函数的线性拟合Fig.2 L inear denotation of the nonsmooth concave function

图2中,OB为ki(xi)=kixi,ki=ci(ai)/ai。用ki(xi)代替ci(xi),则模型(1)可以转化为以下模型:

定理1 当x分别为模型(1)和模型(2)的可行解,则

证明:因为ci(xi)为凹函数,所以ci(xi)≥kixi,则

即

证毕。

假设模型(2)的最优解为x0=(x10,…,xn0)T,如果

证明:由于x0为模型(2)的最优解,则x0是模型(1)的可行解;又因为x＊为模型(1)的最优解,所以f(x＊)≤f(x0)。x＊是模型(2)的可行解,根据定理1可知,g0(x＊)≤f(x＊),因此

即模型(1)的解是收敛的。证毕。

若式(4)不成立,则对ci(xi)与kixi差额最大变量进行分枝。设

令

cs(xs)可通过cs1(xs1)和cs2(xs2)线性拟合,如图3所示。

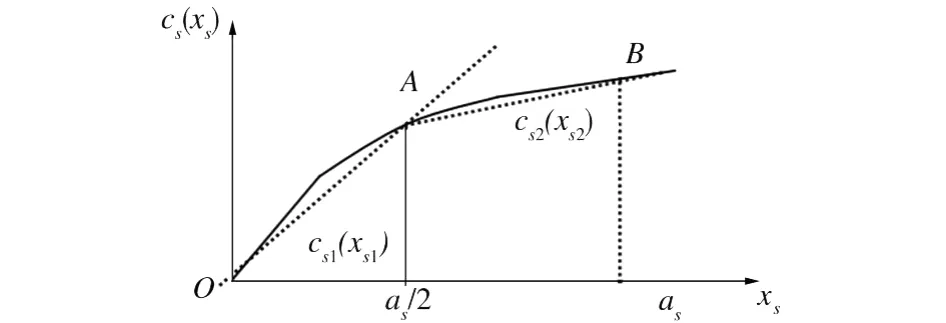
图3 非光滑凹函数分段线性拟合Fig.3 Subsection linear denotation of the nonsmooth concave function

图3中,直线OA为cs1(xs1),斜率ks1=cs(xs1/2)/(xs1/2);直线AB为cs2(xs2),斜率ks2=(cs(as)-cs(as/2))/(as/2)。则模型(2)可转化为下列两个模型:

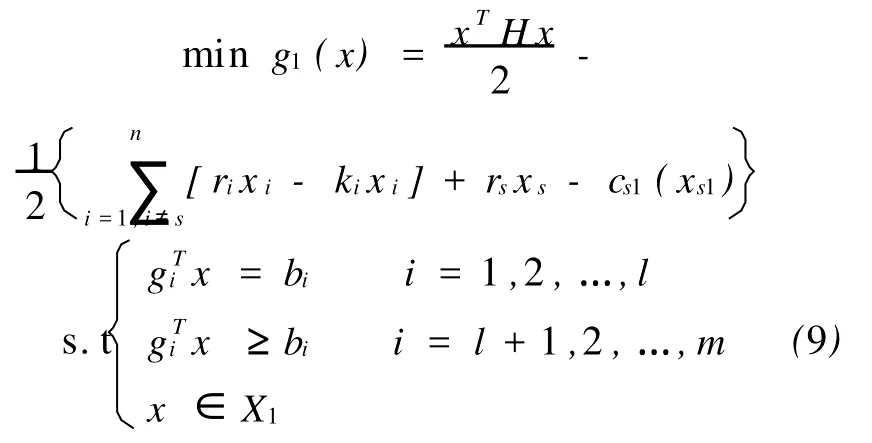
和

定理3 若x1为模型(9)的最优解,则有

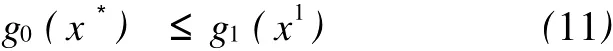
证明:由于x1为模型(9)的最优解,则x1为模型(2)的可行解。又由于所以

由于x＊为模型(2)的最优解,则x1为模型(2)的可行解,故有

由式(12)和式(13)可知

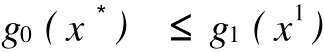
证毕。

由定理3可知,用cs1(xs1)和cs2(xs2)代替cs(xs)以后,目标函数将变大。若为任意小的正数,则x1为模型(1)的近似最优解。

2 算法的基本步骤

2.1 模型(1)的计算步骤

步骤2 如果P={φ},那么转步骤9,否则转步骤3。

步骤3 选择一个问题(Pk)犘

步骤4 让ki(xi)近似估计ci(xi),且Xk=下述数学规划问题可转化为

并转步骤3

步骤9 停止计算就是模型(1)的最优解。

3 结语

提出了一类线性约束下非光滑非线性规划问题,运用分块法和不等式组的旋转算法对该问题进行了求解,同时证明了该算法的收敛性和有效性。

[1] Zangwill WI.A decomposable nonlinear programming approach[J].Operations Research,1967,15(6):1 068-1 087.

[2] Spedicato E,Xia Z Q,Zhang L W.ABS algorithms for linear equations and optimization[J].Journal of Computational and Applied Mathematics,2000,124(12),155-170.

[3] Linderoth J.A simplicial branch-and-bound algorithm for solving quadratically constrained quadratic programs[J].Math Programming,2005,103(2):251-282.

[4] Vandenbussche D,Nemhauser G L.A branch-andcut algo rithm fo r solving nonconvex quadratic prograMS with box constraints[J].Math Programming,2005,102(3):559-575.

[5] Li H M,Zhang K C.A decomposition algorithm for solving large-scale quadratic programming problems[J].Appli Math Comput.2006,173(1):394-403.

[6]Achache M.A new primal-dual path-following method for convex quadratic programming[J].Computational and Applied Mathematics,2006,25(1):97-110.

[7] 王永丽,贺国平,王鑫.求解正定二次规划的一个全局收敛的滤子内点算法[J].数学的实践与认识,2008,21:127-133.

[8] 高岳林,邓光智.凹二次规划问题的一个融合割平面方法的分支定界混合算法[J].工程数学学报,2008(4):589-596.

[9] 赵敏,李少远.基于信赖域二次规划的非线性模型预测控制优化算法[J].控制理论与应用,2009(6):634-640.

[10]夏少刚,费威.具有箱形约束的二次规划的一种简易算法[J].运筹与管理,2008(4):6-10.

[11]张鹏.不允许卖空情况下均值-方差和均值-VaR投资组合比较研究[J].中国管理科学,2008,16(4):7-11.

[12]张鹏,张忠桢,岳超源.基于效用最大化的投资组合旋转算法研究[J].财经研究,2005(12):117-126.

[13]张鹏,张忠桢,曾永泉.限制性卖空的均值-方差投资组合优化[J].数理统计与管理,2008(1):124-129.

[14]张鹏,张忠桢,岳超源.限制性卖空的均值-半绝对偏差投资组合模型及其旋转算法研究[J].中国管理科学,2006,14(2):7-11.