复合固体推进剂静电危险性数值模拟①

鲍 桐,张 炜

(国防科技大学航天与材料工程学院,长沙 410073)

1 引言

作为一种含能材料,固体推进剂对热、机械、冲击波、静电等外界激源具有一定的敏感性。若在储存、运输等过程中受到超过一定强度的外界激源的刺激,其蕴藏的巨大能量可能会以燃烧甚至爆炸的形式释放,酿成灾难性后果。而静电常常是重大事故的罪魁祸首。如1985年1月11日,美国部署在前西德[1,2]的潘兴-2导弹发生爆炸事故,造成3人死亡,16人受伤,损失惨重。事故原因确认为静电放电进入HTPB推进剂药柱,药柱被点燃,并发生爆炸。此后,美、法等国[3,4]十分重视固体推进剂静电危险性的研究。常用的研究方法是试验研究与数值模拟研究,考虑到试验研究的成本与安全问题,数值模拟研究作为相对安全、廉价的研究方法受到越来越多的重视,与试验研究相互验证、补充,已成为一种通行的研究思路。

2 分析计算模型

2.1 物理模型[5]

静电放电(Electrostatic discharge,ESD)被认为是导致固体火箭发动机意外点火的原因之一。固体推进剂放置于绝缘壳体或处于绝缘环境中时,在静电作用下,推进剂内部会产生电场。电场在推进剂内部分布并不均匀[6],当局部电场超过推进剂的击穿强度时,发生静电放电,并释放出能量。

静电放电过程一般是迅速完成的,放电所产生的热量在短时内难以耗散(可看作是一绝热过程),被推进剂所吸收,若达到推进剂的热分解温度,推进剂将分解产生气体产物,并且在局部形成高压气体。在放电过程中或放电过后,高压气体导致推进剂内部出现裂纹。固体推进剂内部的裂纹是否扩展取决于其力学性能。当推进剂强度足够大时,内部的裂纹扩展受到限制,裂纹内的气压可以保持。强度不够时,裂纹内部气体会膨胀,气压和气温不断降低,直到气压等于推进剂的断裂强度,产生了一个短暂的平衡,此时,裂纹扩展终止。

裂纹内部的气体膨胀后尽管温度有所降低,但仍然处于相对高温状态,热量扩散到周围的推进剂中。如果静电放电没有释放出足够的能量,热量耗尽且不引起点火。如果释放出足够的能量,使高温气体引燃裂纹周围推进剂,产生更大的气压,最终导致推进剂的稳定燃烧。固体推进剂静电刺激下危险性发展过程如图1所示。建立传热、传质、裂纹扩展等控制方程对该过程进行描述。

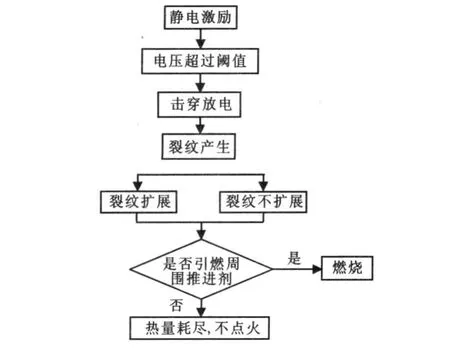
图1 推进剂在静电作用下危险性发展过程Fig.1 Hazard process of propellant under the stimulaction of static electricity

2.2 数学模型

在建立数学模型描述上述静电危险发展过程时,做如下假设:(1)假设推进剂是均一的物质;(2)现实的裂纹形状非常复杂,且不规则,难以描述,因此采用币状裂纹假设,如图2所示,裂纹半径r远大于厚度h;(3)假设裂纹内的气体为理想气体;(4)假设静电放电所释放的能量被推进剂完全吸收,不考虑放电过程中的能量损耗。

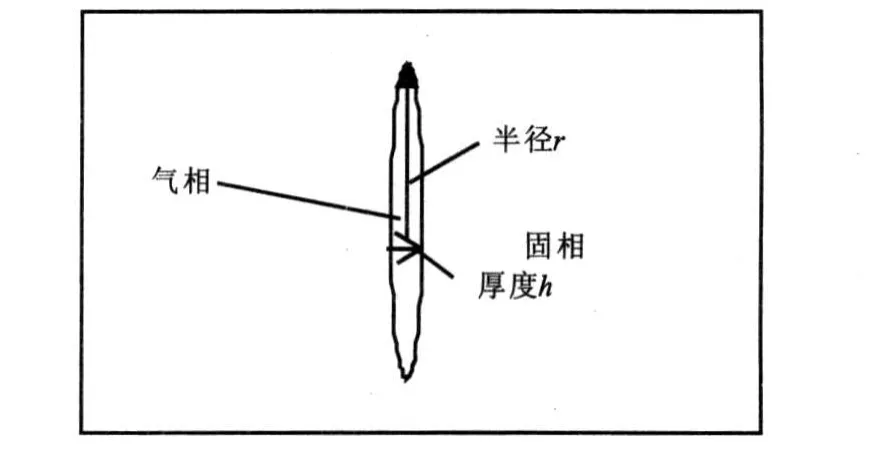
图2 币状裂纹假设示意图Fig.2 Sketch map of coin shape crack hypothesis

建立模型时需要对固相和气相分别建立控制方程。在传热传质计算的研究中,广泛采用的一维非稳态对流-扩散方程在直角坐标系中的形式为[7]

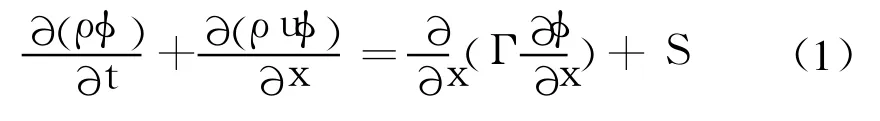
式中 ρ为介质的密度;u为质点在x方向的速度分量;φ为广义变量(质量分数、温度、速度分量等);Γ为对应于φ的广义扩散系数;S为广义源项。

方程(1)中的4项分别为不稳态项、对流项、扩散项和源项。在方程(1)中取φ=1,S=0,ρ为常数,得到固相传质控制方程:

式中 up为固相向界面移动的速度。

如图3所示,将气、固两相界面定为坐标原点,推进剂固相发生热分解时,气相区扩大,若规定界面固定不动,固相区中的质点可视作向该界面移动。式(2)表示同一时刻,固相中各点向界面移动的速度相等。该速度与局部区域内固相的燃面退却速度大小相等,符号相反,在计算中的数值取推进剂的燃速值:

由于裂纹厚度h远小于半径r,在建立控制方程时假设气相与固相的界面是平面(如图3所示)。

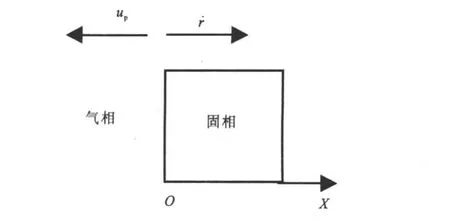
图3 气固相界面示意图Fig.3 Schematic diagram of interface between solid-phase and gas-phase

取方程(1)中φ为固相温度,ρ=ρp,u=up,Гp=λp/,得到固相传热控制方程:

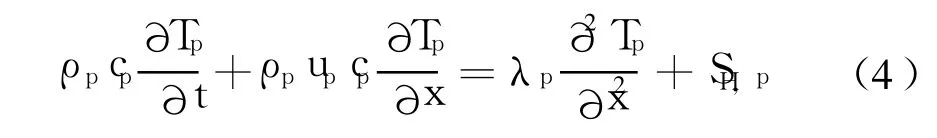
式中 Tp(t)为固相温度;λp为固相物质的热导率;cp为固相的比热容;SH,p为源项。

因为固相中的高温区域集中在气固界面附近,在边界条件中考虑气相的反馈热和固相分解热对固相的加温作用即可,故方程(4)中源项不考虑使固相温度升高的因素,源项SH,p中只包含由于产生裂纹及裂纹传播导致固相降温效应:

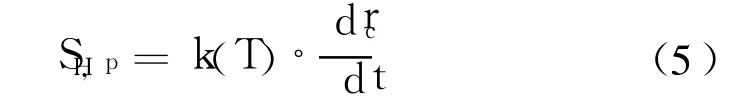
式中 k(T)是与温度有关的系数;rc为裂纹半径,由裂纹传播引起的固相降温效应与裂纹扩展速度drc/dt有关。

气相传质控制方程:在方程(1)中取φ=1,ρ=ρg,u=ug,得:

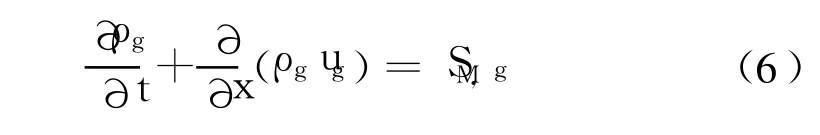
其中,SM,g包含由裂纹扩展引起的气相密度降低,经推导得

式中 Ac为裂纹面积。

气相传热控制方程:在方程(1)中取φ=Tg,ρ=ρg,u=ug,Гg=λg/cg,得

式中 Tg(t)表示气相温度;cg表示裂纹内气相物质的比热容;λg表示气相产物的热导率。

裂纹内的气相物质一方面会发生化学反应放热,另一方面静电放电的能量对气相物质也有加热作用,因此源项SH,g应包含这两方面的影响:

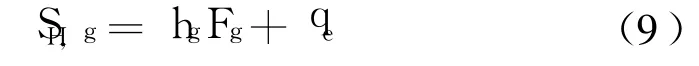
式中 hg为气相物质的化学反应热;Fg为气相物质的反应速率;qe表示单位体积气体中的放电能量,qe=We/Vc,Vc为裂纹区的体积,We为静电放电功率,是时间t的函数。

根据文献[8]报道,We服从如图4所示的特征曲线。该曲线可用以下形式的方程描述:

式中 Qe为放电总能量;τ为放电时间常数。

求解上述方程所需的定解条件如下:

(1)边界条件

气、固界面上质量守恒,即从固相离开的质量等于通过界面进入气相的质量:

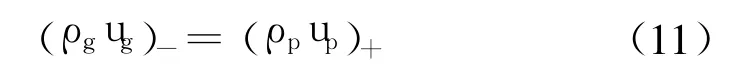
如图3所示,界面上“-”为气相区域,“+”为固相区。

气、固界面上热流连续,气相传出的热量等于传入到固相的热与固体的分解热之和:

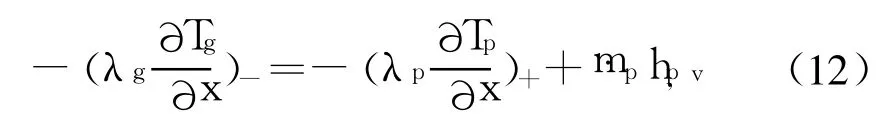
式中 m·p为单位面积上物质由固相进入气相的质量流量;hp,v为单位质量固体推进剂的分解热。

界面上温度连续:

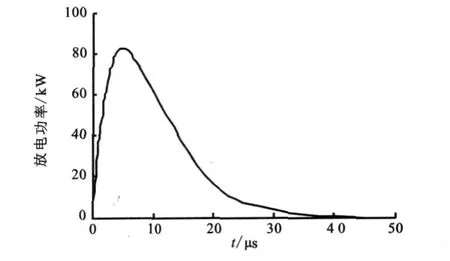
图4 静电放电能量释放特征曲线Fig.4 Characteristic curve of energy release during electrostatic discharge

(2)初始条件

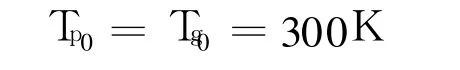
上述分析计算模型中涉及的多个偏微分方程难以获得解析解,必须采用数值解法,常用的思路是采取一定的离散化方法,将偏微分方程转化为代数方程求解。本文采用经典的控制容积法获得离散化的代数方程,并编制了相应的计算程序求解。

在完成一个时间步长的计算,获得Tg、Tp等计算结果后,需要判断裂纹是否扩展,如果扩展,计算扩展后裂纹尺寸。基于线弹性断裂力学模型,计算应力强度因子由方程(14)定义[8]:

式中 σ为垂直裂纹面方向的应力值,与裂纹内气体压强有关;rc为裂纹半径。

如果应力强度因子超过断裂韧性(KIC),裂纹就会产生并扩展,裂纹扩展速率由方程(15)表示:

若裂纹扩展,裂纹半径会增大,ρg、Tg、Tp等数值也会随之发生变化,因此完成裂纹扩展的计算后,需要对ρg、Tg、Tp的数值进行修正,以修正后的结果作为下一步计算的初始值。如此循环求解直至推进剂发生危险性变化(被点燃),或达到安全的状态,这取决于静电放电输入能量(Qe)的大小。

3 计算结果与分析

3.1 模型验证

根据2.2中分析计算模型,对文献[5]所报道的HTPB推进剂发生危险性变化的静电放电临界能量进行求算,将计算结果与文献中报道的计算结果进行比较,以此衡量该模型的准确性。

文献[5]报道的HTPB推进剂发生危险性变化的静电放电临界能量为0.76 J。本研究采用该文献中报道的有关推进剂性能参数(如表1所示),计算结果如图5所示。当静电放电能量低于0.74 J时,在静电的激励下,推进剂内有热点形成,但热点的温度会缓慢下降,推进剂不会发生自维持燃烧,因此推进剂发生危险性变化的临界能量为0.74 J,与文献值接近,说明本研究所采用的分析计算模型较准确,可以用于固体推进剂在静电作用下危险性的数值模拟研究。

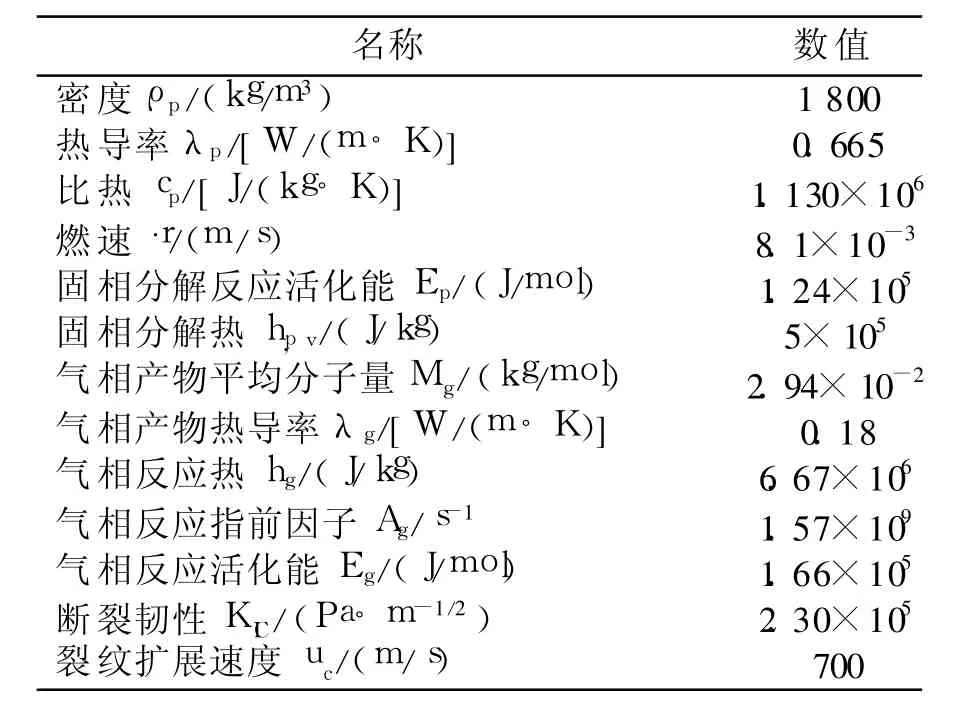
表1 验证计算用推进剂主要性能参数Table 1 Propellant data used in validating calcu lation

3.2 固体推进剂静电危险性影响因素

在模型准确性得到验证的基础上,考察了某推进剂的特性参数(如弹性模量、断裂韧性、裂纹扩展速度、固相分解热、燃速等)及静电能量加载方式(如放电时间等)等因素对临界能量的影响规律,其中放电时间、断裂韧性、裂纹扩展速度、燃速对临界能量的影响较大。

3.2.1 放电时间

不同放电时间下,固体推进剂发生危险性变化的临界放电能量和临界放电功率如表2所示。

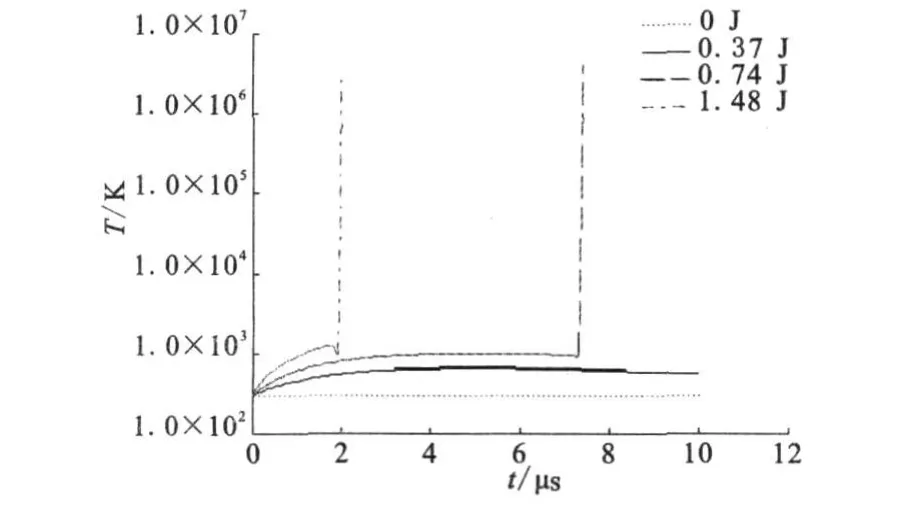
图5 推进剂内部静电作用区域的温度-时间曲线Fig.5 Temperature-tim e curve of electrostatic effect area inside the p ropellant

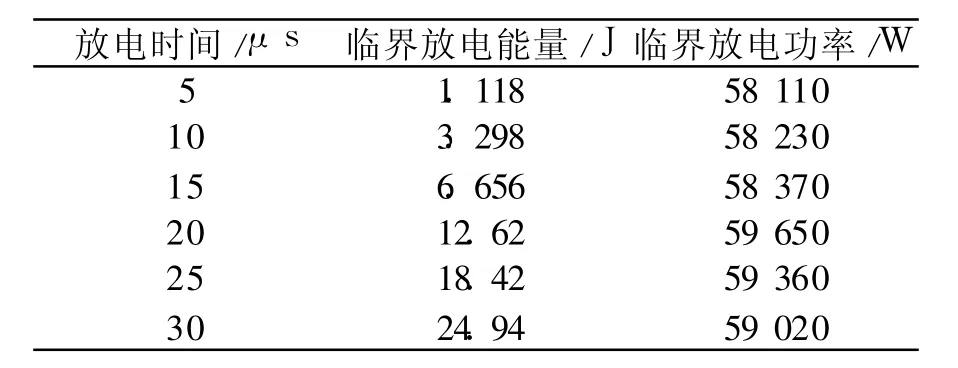
表2 不同放电时间下的临界放电能量和临界放电功率Table 2 Critical discharge energy and power at different discharge time

当其他条件固定,仅改变放电时间时,随着放电时间的延长,临界放电能量增加,而临界放电功率基本保持一致,计算所得引起固体推进剂发生危险性变化的临界放电功率约为58 790W。这表明与放电能量相比,放电功率可能是更为准确的危险性评价标准,只有当推进剂受到一定强度的能量输入时,才会发生危险,因此在较长的放电时间内,只有输入更多的能量,才可以达到一定的放电功率。

3.2.2 断裂韧性

其他参数固定,KIC改变时,固体推进剂发生危险性变化的临界放电能量和临界放电功率如表3所示。计算结果表明,临界放电能量与临界放电功率均随断裂韧性的增大而减小。分析其原因,一方面式(14)和式(15)表明KIC越大,引起裂纹扩展所需应力σ越大,相应地,裂纹扩展之前,裂纹内气体所能保持的压强和温度也越大,有利于热点区的形成与保持,推进剂越容易被引燃;另一方面从固相传热方程来看,式(4)中SH,p与裂纹产生及传播导致的固相降温效应有关,KIC越大,裂纹越难以扩展,相应的降温效应越低,推进剂越容易发生危险。注意到表3中最后3组的计算结果相同,这表明无论断裂韧性的数值多大,推进剂都必须受到足够大的能量用于加热并引燃,才会发生危险性变化,而这3组的计算结果正是该最低能量。

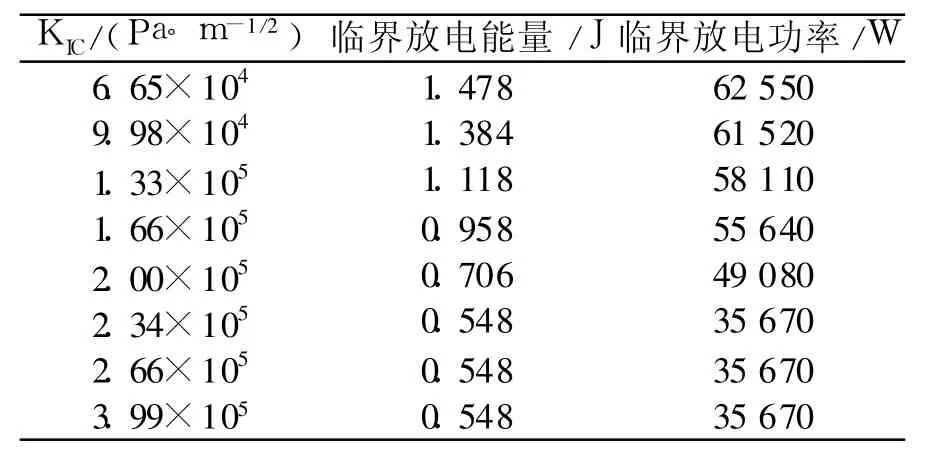
表3 不同断裂韧性推进剂的临界放电能量和临界放电功率Table 3 C ritical discharge energy and pow er at different fracture toughness

3.2.3 裂纹扩展速率

其他参数固定,裂纹扩展速率改变时,固体推进剂发生危险性变化的临界放电能量和临界放电功率如表4所示。计算结果表明,临界放电能量与临界放电功率均随裂纹扩展速率的增大而增大。分析其原因,一方面式(14)和式(15)表明uc越大,KI＞KIC时裂纹扩展得越快,而裂纹的扩展会导致裂纹内气体的压强和温度降低,裂纹扩展得越快,裂纹内气体越难保持高压和高温,不利于热点区的形成与保持,推进剂越难以引燃;另一方面从固相传热方程来看,式(4)中SH,p与drc/dt成正比,裂纹扩展时uc越大,由此导致的固相降温效应越大,推进剂越难以发生危险。

表4 不同裂纹扩展速率推进剂的临界放电能量和临界放电功率Tab le 4 C ritical discharge energy and power at different crack propagation velocity

3.2.4 燃速

表5列出了不同燃速的固体推进剂发生危险性变化的临界放电能和临界放电功率。当其他条件不变,燃速大的推进剂,在同等条件下会有更多的固相推进剂转化为气相产物,裂纹内可以获得更高的气压,同时燃烧反应所释放的热量更多,有利于热点的形成和发展,因此发生危险性变化的临界能量和功率小于燃速低的推进剂。一般认为同等条件下,高燃速推进剂往往比低燃速推进剂危险,在研制、使用过程中需要特别加以注意。

表5 不同燃速推进剂的临界放电能量和临界放电功率Table 5 Critical discharge energy and power at different burning rate

4 结论

建立了一种复合固体推进剂静电危险性数值模拟方法,考察了某推进剂的特征参数对该推进剂发生危险时的临界放电能量和功率的影响规律。研究表明,力学性能较好(断裂韧性大、裂纹扩展速率低)及燃速较高的推进剂配方容易在静电激励下发生危险,需在配方设计中加以注意。与静电感度测试方法相比,数值模拟研究相对安全、廉价,可作为试验研究的有效补充,有利于加深对固体推进剂静电危险性的认识,为推进剂的安全使用提供帮助。

[1] 候林法.复合固体推进剂[M].北京:宇航出版社,1994.

[2] Davenans A,Ratsnpe R.Sensitivity of solid rocket motors to electrostatic discharge:history and future[R].AIAA 99-2930.

[3] Mellor A M,Stoops D R.Optimization of spark and ESD propellant sensitivity test.A review[J].Propellants,Explosives,Pyrotechnics,1990,15:11.

[4] Auzazeau M,Roux M.Electric spark and ESD sensitivity of reactive solids.Part one[J].Propellants,Exp losives,Pyrotechnics,1993,18:317.

[5] Raun R L.Modeling of ESD-induced confined ignition of solid rocket propellants[J].Combustion and Flame,2000,120:107-124.

[6] Gyure M F,Beale P D.Dielectric breakdown of a random array of conducting cylinders[J].Physical Review B,1989,40:39-46.

[7] 陶文铨.数值传热学[M].西安:西安交通大学出版社,2001.

[8] Hodges R V,McCoy L E,Raun R L.Workshop on propellant ignition micro mechanics proceedings[C].1991:199-213.

[9] 杨卫.宏微观断裂力学[M].北京:国防工业出版社,1995.