Kendall协调系数W检验及其SPSS实现*1

程 琮 刘一志 王如德

(1.泰山医学院卫生统计学教研室，2.统计学教研室, 山东 泰安 271016；3.临沂市疾病预防控制中心，山东 临沂 276001)

1 基本原理和方法

1.1基本概念

在等级资料或非正态分布的数据中，研究人员经常对观察对象的不同类型的能力进行评分，观察不同能力之间的评分是否具有一致性。此类数据属于双因素设计，即为多样本相关数据的分析。可应用Kendall协调系数W检验(Kendall’s coefficient of concordance W)的分析方法。该检验由Kendall 和Babington-Smith在1939年提出。

资料类型及特点：设有b个评判员(区组)，对k个观察对象或观察指标(处理组)进行评分。按照每个评判员的评分，对k个观察对象或观察指标的评分由小到大编排秩次。秩次为从1，2，…，k。数据见表1。表1显示：共有k=10个学生为观察对象。由b=6个专家对每个学生6个方面的学习能力给予评分，表1中的数值不是原始评分数据，而是根据评分已经编排好的秩次。

1.2应用条件

(1)数据由k个观察对象及b种测试能力或b个评判员的评分构成。

(2)测量尺度至少是顺序尺度。

(3)观察值可以为原始评分的数据，也可以是对原始数据编排的秩次。

1.3基本原理

检验假设 H0：b组秩次没有一致性；H1：b组秩次存在一致性。

检验统计量W计算公式为：

(1)

式中： b是评判个数。k是观察对象或观察指标个数。Rj是分配给第j个观察对象的秩次的合计。

如果b种学习才能或特征之间无相关，则各列出现的秩次值是随机的。期望的各列合计值近似相等。如果b种特征之间存在相关，则期望的某些列有较大的秩次，而另一些列则有较小的秩次。当H0成立时，则理论上各列的合计值相等，如表1数据的各列合计值等于330/10=33，则6个特征之间无相关。本例，计算的离均差平方和S的观察值为：

S=(28-33)2+(25-33)2+…+(45-33)2=514

在6种学习能力中，如果每个学生有相同的能力，则应得到相同的评分和秩次。例如，若第一个学生在机械能力方面编排秩次为1，则在艺术才能方面也编排秩次为1，其它各才能方面编排秩次均为1，则秩次之和为6×1=6；第二个学生各能力方面均编排秩次为2，则秩次之和为6×2=12。余类推。

如果各个能力方面完全相关，则各列秩和为：

第1列秩和为：6×1=6，

第2列秩和为：6×2=12，

第3列秩和为：6×3=18，

……

第10列秩和为：6×10=60，

此时，离均差平方和S的期望值为：

S=(6-33)2+(12-33)2+…+(60-33)2=2970

将本例的S观察值与S期望值相比，有：

若存在完全一致性，则其比值为1。若完全没有一致性，则比值为0(由于分子为0)。介于0和1之间，则有一定程度的相关性。

计算S的公式为：

(2)

公式中符号意义，见公式(1)。如果各组秩次有完全一致性，则列合计为1b,2b,…kb,但可以不按顺序排列。各列与期望值之差的平方和，公式为：

(3)

公式(2)与公式(3)之比，即为检验统计量W：

(4)

经过适当的数学变换，公式(4)可以变换为公式(1)。两者等价。

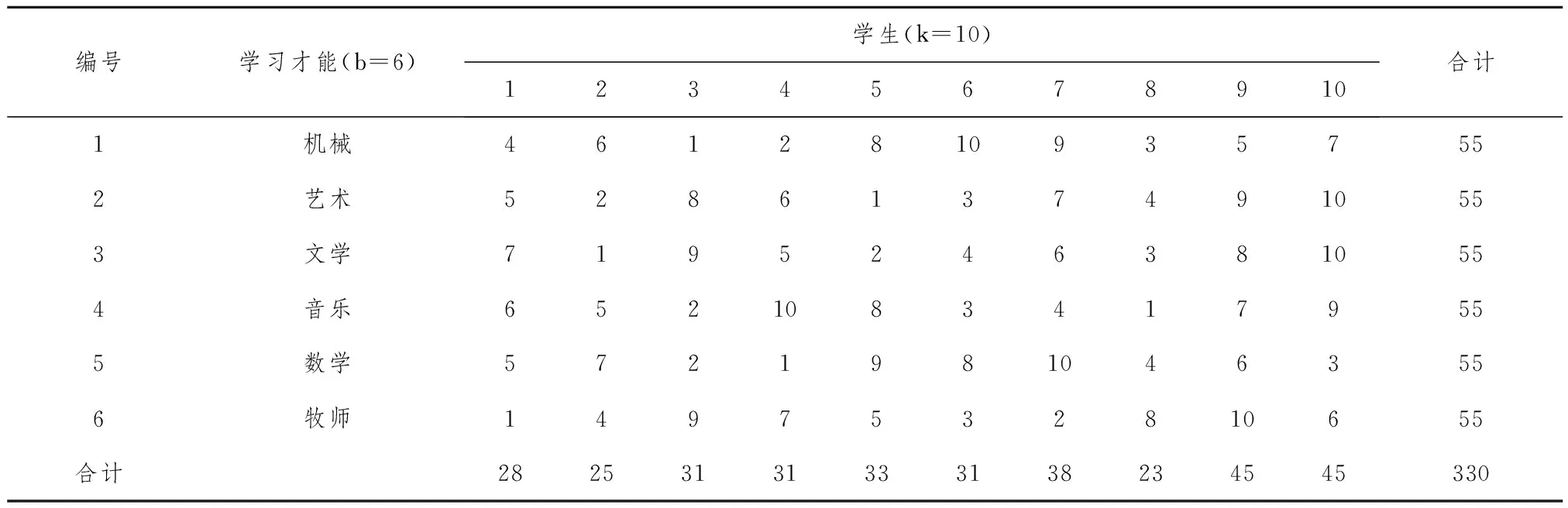
表1 6名专家对10名学生学习能力的评分(秩次)

1.4出现相同数据

若出现2个或更多个相同数据时，计算平均秩次。公式(1)中分母被替换为下式：

b2k(k2-1)-bΣ(t3-t)

(5)

校正的Wc公式为：

(6)

式中：t为相同数据的个数。

1.5判断原则

当观察的各组秩次接近一致时，S值倾向于更大。当S值较大时，W值也较大，倾向于1。当观察的各组秩次不一致时，S值倾向于更小。当S值较小时，W值也较小，倾向于0。当W值充分大时，结果将导致拒绝没有一致性的无效假设。

当b和k较小时，可以根据α、b、k和W值，查Kendall协调系数W值表，判断结论。

如果b、k值超出Kendall协调系数W值表，则应用大样本近似法计算卡方值，并根据自由度υ=k-1，查阅卡方界值表作出判断和结论。Kendall推荐当k>7时，计算卡方值。卡方值计算公式为

χ2=b(k-1)W

(7)

2 实 例

2.1应用公式计算

例1 研究人员对戒酒中心的15名病人进行调查。让病人对戒酒计划中的10项指标给出评分。数据见表2。表2中的数据是对评分编排的秩次。试分析戒酒中心的病人对戒酒计划其中的10项指标的评分是否具有一致性。

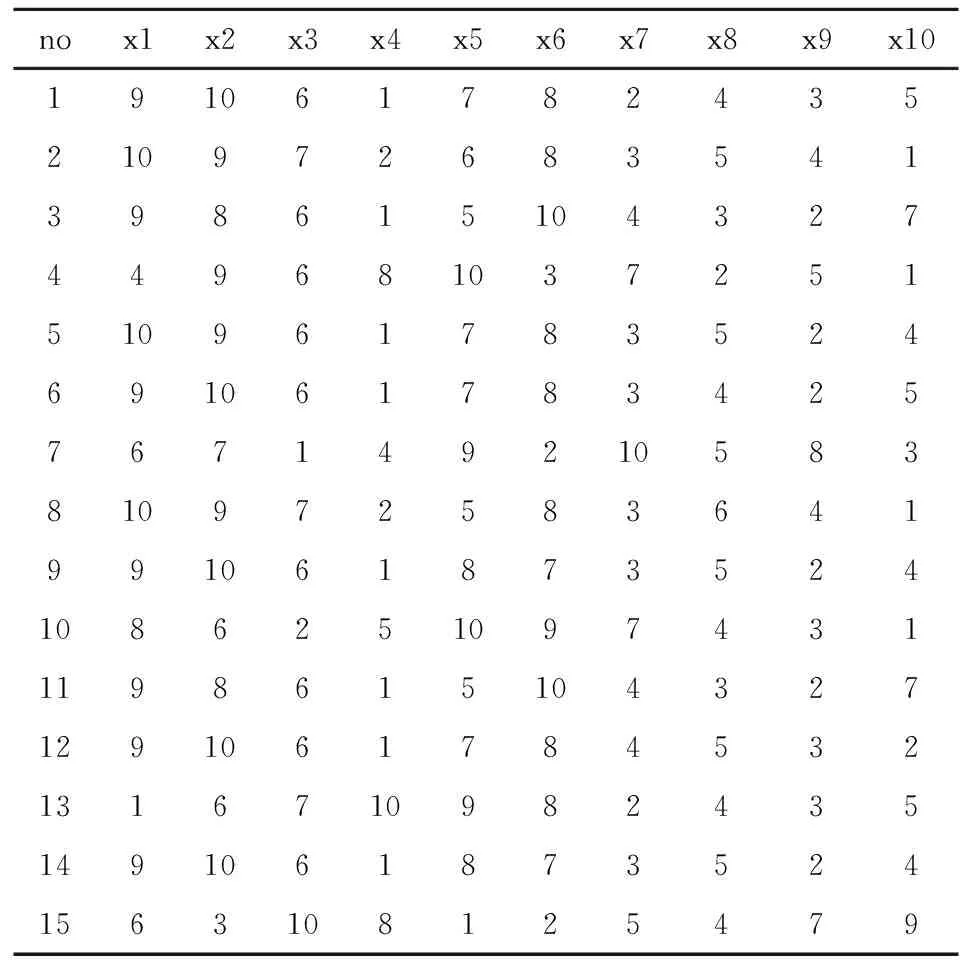
表2 Kendall协调系数W检验数据

表2中：no为编号，即为15个病人。x1～x10为10个评价指标。

检验步骤如下：

(1)建立检验假设

H0：病人对10项指标的评分没有一致性；

H1：病人对10项指标的评分存在一致性。

α=0.05。

(2)计算检验统计量

将各列数据合计后平方再相加，有下列计算结果：

代入公式(1)有：

=0.4036

(3)确定P值，推断结论

由于b=15，k=10，超出Kendall W一致性系数表范围，可应用大样本近似法计算卡方值：

χ2=b(k-1)W=15(10-1)0.4036=54.486

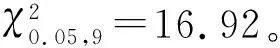
结论：可以认为15个病人对10项指标的评分具有一致性。

例2 3个监督员为5个雇员的工作能力进行评分。分值最低为1分，最高为10分。见表3。

表3 3个监督员为5个雇员工作能力评分(秩次)

注意：表3中的数据为3个监督员的评分值，括号中数据为编排的秩次。对每个监督员的评分值横向编排秩次。第1个监督员有两个相同的评分即2分，求平均秩次为1.5。则t1=2。第3个监督员也有两个相同的评分，求平均秩次为3.5。则t2=2。

当出现相同数据时，计算校正的统计量Wc。

Σ(t3-t)=(23-2)+(23-2)=12

根据b=3，k=5，查Kendall W一致性系数表，当近似界值W=0.733时，P=0.038。由于P<0.05，拒绝H0，接受H1。可以认为3个监督员对5个雇员工作能力的评分具有一致性。

注意： Kendall W一致性系数表中的W界值不一定与计算的统计量W值完全相同，可以取相近的W界值即可。

2.2应用SPSS13.0统计软件计算

操作步骤如下:

1.建立数据文件

输入数据模式见表2数据。注意：将所有变量定义为数值型变量。

2.运行非参数的“K Related Samples过程”

(1)打开待分析的数据文件，见表2数据；

(2)在SPSS Data Editor窗口中，依次选择：Analyze→Nonparametric Tests→K Related Samples→显示“Tests for Several Related Samples”主对话框：进行参数设置。见图1。

(3)在“Test Varibles”框中：选入“x1～x10”；

(4)选定“Kendall’s W”复选框；

(5)单击“OK”按钮，运行该过程。

图1 Tests for Several Related Samples过程对话框

3.显示“K Related Samples”过程结果

结果中显示两个表。

(1)Ranks表：显示x1～x10这10个指标的平均秩次。

(2)Test Statistics表：显示N为15例，Kendall’s W值为0.404，卡方(Chi-Square)值为54.491。P值(Asymp. Sig.)为0.000。结果与例1中用公式计算的相同，只是在第2位或第3位小数上有一点差别。

3 小 结

Kendall协调系数W检验是一种非参数检验方法，用于双因素设计资料的一致性检验。其基本原理是由b个评判员对k个观察对象或观察指标进行评分，然后检验b个评判员的评价结果是否具有一致性。此方法在医学心理测量指标及调查表中调查项目或指标的评价中应用广泛。可使用SPSS统计分析软件进行分析。

[1] Wayne W Daniel. Applied nonparametric statistics[J]. 2th edition. Boston: PWS-KENT Punlishing Company,1990:386-391.

[2] 程琮. SPSS统计分析教程[M]. 北京:现代教育出版社,2009.