(p，q)型Minkowski空间的双曲Euler公式与反向Schwarz不等式

李武明,许 宁

(通化师范学院 数学系,吉林 通化 134002)

1 问题的提出

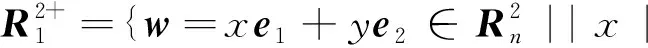
仅当x=0时等号成立}

exp(e1e2φ)=coshφ+e1e2sinhφ

(1)

(2)

其中φ=arctanh(|x|/y).

(3)

成立.

如上结论也适用于n维Minkowski空间[6-7]

xnen|xi∈R,i=1,…,n}

其中e1,…,en-1,en为其M-正交基.

2 定义与例子

Clifford代数Clp,q的生成空间[1,8]

Rp,q={x1e1+…+xpep+xp+1ep+1…+

xp+qep+q|xi∈R,i=1,…,p+q=n}

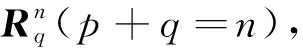
例1 前述Minkowski平面为(1,1)型Minkowski空间，n维Minkowski空间为(n-1,1)型Minkowski空间.

事实上，每个(p,q)型Minkowski空间均可看作一个(p,0)型Minkowski空间与一个(0,q)型Minkowski空间的直和.令

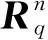
3 主要结果

由M-内积定义w的模为

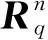
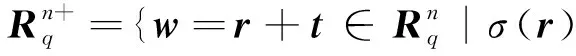
r=0时等号成立;xp+1,…,xp+q≥0}.

利用双曲函数式及指数函数式

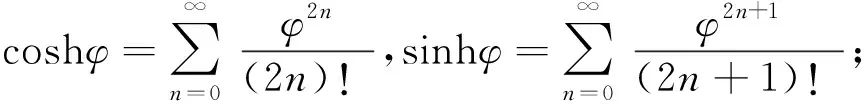
可导出如下定理.

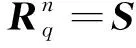
exp(r0t0φ)=coshφ+r0t0sinhφ

w=t0σ(w)exp(r0t0φ)及

w=σ(w)(r0sinhφ+t0coshφ),

其中φ=arctanh(σ(r)/σ(t))；t0,r0依次为与t,r同向的单位向量.

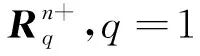
定理5 任取r1,r2∈S存在t1,t2∈T,使得

证明 设r1,r2∈S+取a=2max{|r1|,|r2|}+1,

则t1=aep+1,t2=aep+2∈T+,w1=r1+t1，

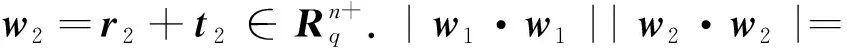
故命题成立.

成立.

参考文献：

[1]Lounesto P.Clifford algebra and spinors [M].Cambridge University Press,2001.

[2]Baylis W E.Clifford(Geometric) algebra with applications to Physics, mathematics, and engineering[M].NewYork:Birkhauser Boston,1996.

[3]李武明.时空平面的Clifford代数与Abel复数系统[J].吉林大学自然科学学报,2007(5): 13-16.

[4]李武明.Clifford代数与Minkowski空间的性质[J].吉林大学学报, 2000,13(4):13-16.

[5] Li Wuming, Yang Fan.N-dimensional Minkowski space and space-time algebra[J].New Zealand Journal of Mathematics,2004:159-164.

[6] Li Wuming, Yang Fan.N-dimensional space-time unit spheres and lorentz Transformation[J].Advances in Applied Clifford Algebra,2003:57-64.

[7]吴亚波,邵颖.双曲复数与双曲复群在1+1维相对论时空中的应用[J].辽宁师范大学学学报,2001(1).

[8]Zhang Shuna.Clifford Algebra and the Lorentz Transformation with(p,q) Form[J].Advances in Applied Clifford Algebra,2005(2):39-43.