不对称双塔楼结构连接控制方案比较研究

蔡 振， 谭可可， 閤东东

(1.第二炮兵工程设计研究院， 北京 100011; 2.北京市建筑设计研究院， 北京 100045)

现代城市中体型复杂的多功能高层建筑越来越多，比较典型的如带大底盘的多塔楼高层建筑，由于裙房的存在，多塔楼高层建筑结构的动力特性非常复杂。这类建筑结构为了美观，通常在塔楼之间采用空中连廊进行连接。空中连廊的设计非常复杂，如果连廊刚度过大，会对原有塔楼结构的动力特性产生很大影响，如果连廊刚度过小，其抗风设计问题很难解决。如果采用阻尼器代替连廊，则能够利用各塔楼之间的相对运动耗能减震，并且不用考虑连廊的设计问题。现有绝大部分研究局限于相邻的单体建筑结构，有必要对相邻结构振动控制体系在大底盘的多塔楼高层建筑结构中的应用进行研究。

国内外已有众多学者对相邻结构间安装控制装置减震进行了研究，朱宏平等将两相邻结构简化为两单自由度体系，采用Maxwell型粘滞流体阻尼器连接，导出了在地面白噪声激励下流体阻尼器的优化参数的一般表达式[1]。Xu等将粘滞流体阻尼器运用到相邻结构的振动控制中，通过大量数值分析，获得了使结构振动响应减小最大的优化控制参数[2]，并进行了实验研究[3]。Christenson采用弯曲悬臂梁模拟两相邻超高层建筑，采用被动、半主动和主动控制的方法对两结构进行耗能减震[4,5]。Abdullah[6]在2001年提出在相邻结构间安装共享调谐质量阻尼器STMD(Sheared Tuned Mass Damper)进行耗能减震。

相邻两单体建筑结构间的连接Maxwell型阻尼器参数可以通过显式表达式求出[7,8]，由于裙房的影响，该表达式能否用于带裙房不对称双塔楼高层建筑结构连接控制方案中是一个值得研究的问题。STMD方案与仅采用阻尼器连接的控制方案对比，究竟孰优孰劣是一个值得关注的问题。因此，本文以带裙房不对称双塔楼高层建筑结构为例，对以上问题进行了研究。

1 不对称双塔楼结构计算模型

1.1 被动控制单元模型

Maxwell模型如图1所示，由阻尼元件与弹簧串联组成，当阻尼装置表现出具有依赖频率的性质时，选用Maxwell模型可以得到更为精确的结果。

图1 Maxwell模型

Maxwell型阻尼器产生的控制力计算式如下

(1)

1.2 阻尼器连接结构运动方程

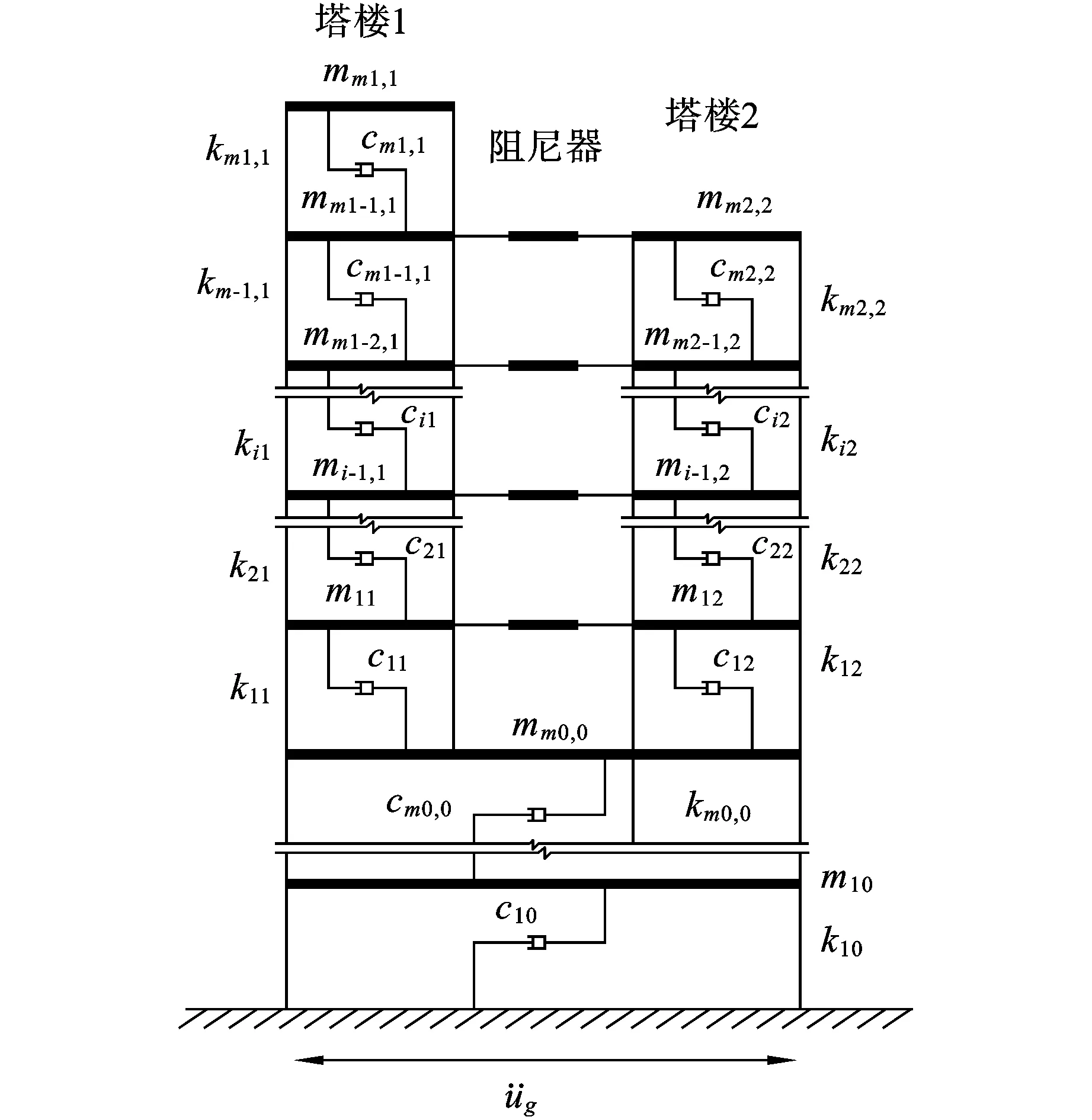
图2 大底盘不对称双塔楼结构阻尼器连接控制计算模型

如图2所示，大底盘不对称双塔楼结构共包括三个部分，分别是层数为m0的裙房，层数为m1的塔楼1和层数为m2的塔楼2，均采用剪切型模型进行建模。假设结构质量集中在楼层，两结构平面对称，只考虑水平向结构沿对称面的地震波作用。结构的运动方程如下

(2a)

(2b)

kij(yij-yi-1,j)+ki+1,j(yij-yi+1,j)+fi(t)

(2c)

(2d)

式中，mi0，ki0和ci0分别为裙房第i层的质量、刚度和阻尼系数；mi1，ki1和ci1分别为塔楼1第层的质量、刚度和阻尼系数；mi2，ki2和ci2分别为塔楼2第i层的质量、刚度和阻尼系数。

1.3 双塔楼结构STMD计算模型

图3 大底盘不对称双塔楼结构STMD计算模型

如图3所示，在高度较低的结构顶部安装共享调谐质量阻尼器STMD，结构的运动方程如下

(3a)

(i≠M,T,j=0,1,2)

(3b)

(i=M,j=0)

(3c)

(3d)

(3e)

式中，裙房、塔楼1和塔楼2的各层参数同前，cij和kij分别为STMD中连接塔楼j的阻尼器弹簧阻尼和刚度系数。

2 数值算例

某塔楼是一栋由裙房和不对称的双塔楼组成的综合型多功能高层建筑，塔楼1(左塔楼)与塔楼2(右塔楼)分别为30、20层，裙房为5层。裙房各楼层集中质量均为2.5×106kg，剪切刚度均为8.0×109N/m，左右塔楼各楼层集中质量均为1.0×106kg，剪切刚度均为4.0×109N/m。显然，塔楼1第一阶自振频率低于塔楼2第一阶自振频率。采用瑞利阻尼模型，结构1与结构2第一、二阶阻尼比均为0.02。过滤白噪声参数取为ωg=15.0 rad/s与ζg=0.6，地面运动激励强度取为S0=4.65×10-4m2/rad·s3。

2.1 连接阻尼器优化参数

特征值分析塔楼1与塔楼2的第一阶自振圆频率分别为2.96和4.41 rad/s，总质量分别为3.0×107和 2.0×107kg。在此忽略了裙房的影响。采用阻尼器的Maxwell模型优化参数表达式[9]，优化阻尼系数等于2.56×107N·s/m，优化松弛时间都等于0。

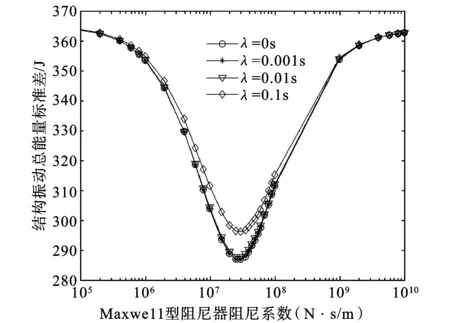
图4 结构振动总能量标准差随阻尼系数变化曲线

图5 结构振动总能量标准差随松弛时间变化曲线

考虑在较低塔楼高度一半处和顶部设置阻尼器，控制目标为减小两塔楼及裙房的地震响应，以Maxwell型阻尼器的零频率阻尼系数和松弛时间作为优化目标，并对其进行参数化研究。结构振动总能量标准差随Maxwell型阻尼器阻尼系数的变化规律如图4所示，从图中可以得到阻尼系数的优化取值约为2.5×107N·s/m，当阻尼系数取值小于1.0×107N·s/m或大于1.0×108N·s/m时，阻尼器控制性能迅速恶化，说明控制效果对阻尼器阻尼系数比较敏感，理论计算结果与参数化分析结果非常吻合。图5表明了结构振动总能量标准差随松弛时间的变化，可看出当Maxwell型阻尼器刚度为其阻尼系数的102倍以上时，松弛时间对控制效果影响很小，理论松弛时间为0和数值分析结论一致。在工程应用中，当Maxwell型粘滞流体阻尼器刚度为阻尼系数的103倍以上时，即表现出纯阻尼行为。通过比较可以发现阻尼器的优化参数数值分析结果与理论解吻合良好，大底盘不对称双塔楼结构间连接阻尼器参数可以通过两塔楼的总质量和前两阶自振圆频率计算得到。

2.2 STMD控制方案优化设计

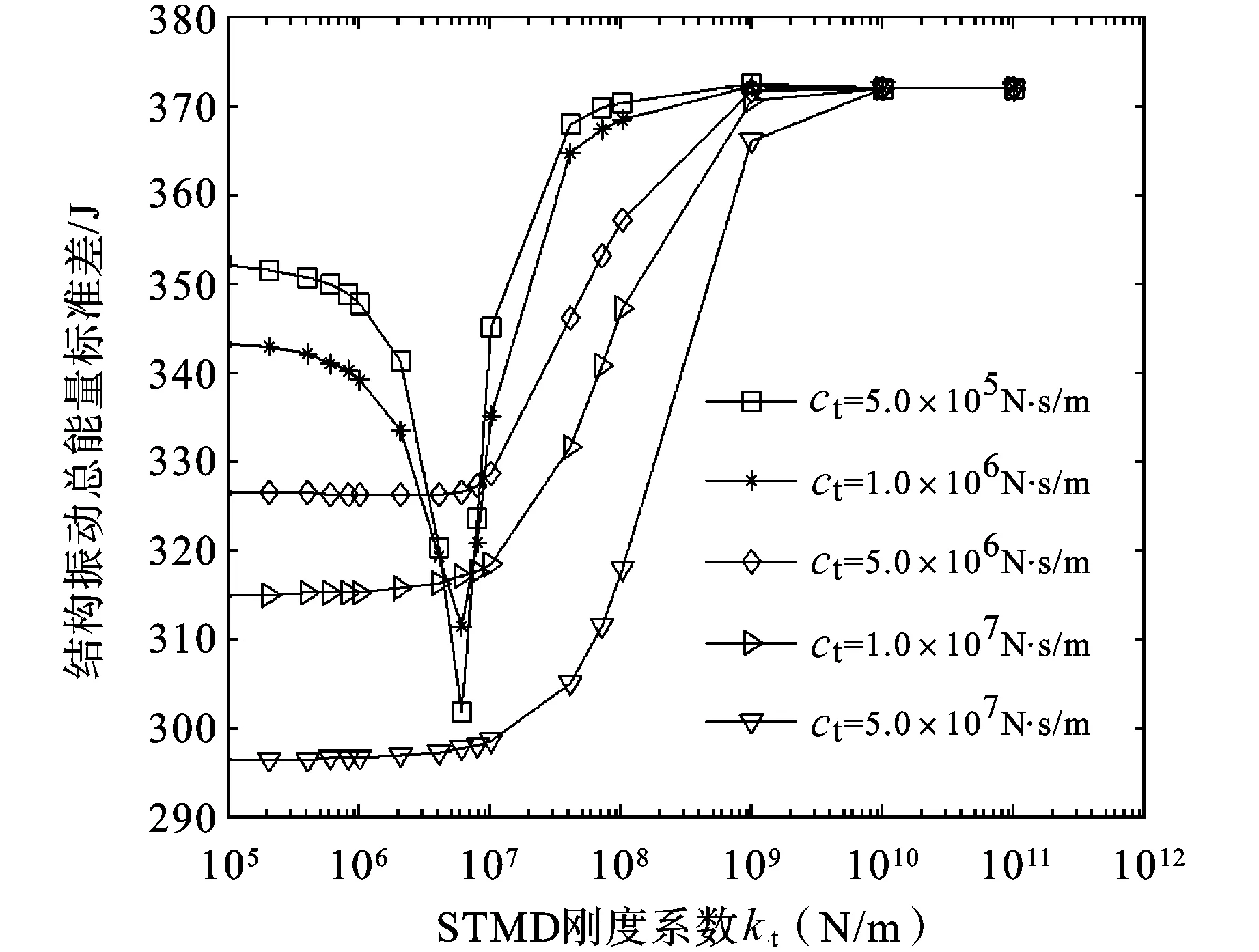
图6 结构振动总能量标准差随STMD刚度系数变化曲线

图7 结构振动总能量标准差随STMD阻尼系数变化曲线

STMD质量块取为1.5×106kg，为塔楼1总质量的5%，安装在塔楼2顶层，并与塔楼1和塔楼2顶层连接，设连接在塔楼1与塔楼2之间阻尼器的刚度系数kt和质量系数ct相同。图6给出了结构振动总能量标准差随STMD刚度系数kt变化曲线，图中表明kt优化取值在6.0×106与7.0×106N/m之间，如果STMD两端的连接弹簧刚度均为6.57×106N/m，则两并联弹簧刚度和为13.14×106N/m，质量块质量为1.5×106kg，则STMD的自振频率为2.96 rad/s，与塔楼1的第一阶自振圆频率吻合。在工程应用中，当TMD的调谐频率与结构第一阶自振频率接近时，可以取得比较理想的控制效果。图7给出了结构振动总能量标准差随STMD阻尼系数ct变化的曲线，显然可以发现优化阻尼系数取值为4.0×107N·s/m。因此STMD两端连接弹簧优化刚度和阻尼系数分别取6.57×106N/m和4.0×107N·s/m。

2.3 频域分析结果

Maxwell型阻尼器优化总阻尼系数取理论值2.56×107N·s/m，松弛时间取0，STMD连接弹簧参数优化刚度和阻尼系数分别取6.57×106N/m和4.0×107N·s/m。下面在频域内对两种控制方案优化设计后的性能进行比较。

图8给出了结构振动总能量功率谱密度比较曲线，从图中可以发现在塔楼的第一阶和第二阶自振频率处，STMD和Maxwell型阻尼器控制效果相当，但是在其他高阶频率处，STMD控制效果明显比Maxwell型阻尼器差，各个频率峰值处仅稍有削弱。和单独TMD控制系统类似，STMD对双塔楼高阶频率的响应无能为力。相同的现象可以从图9中观察到，其中给出了裙房底层基底剪力功率谱密度曲线。

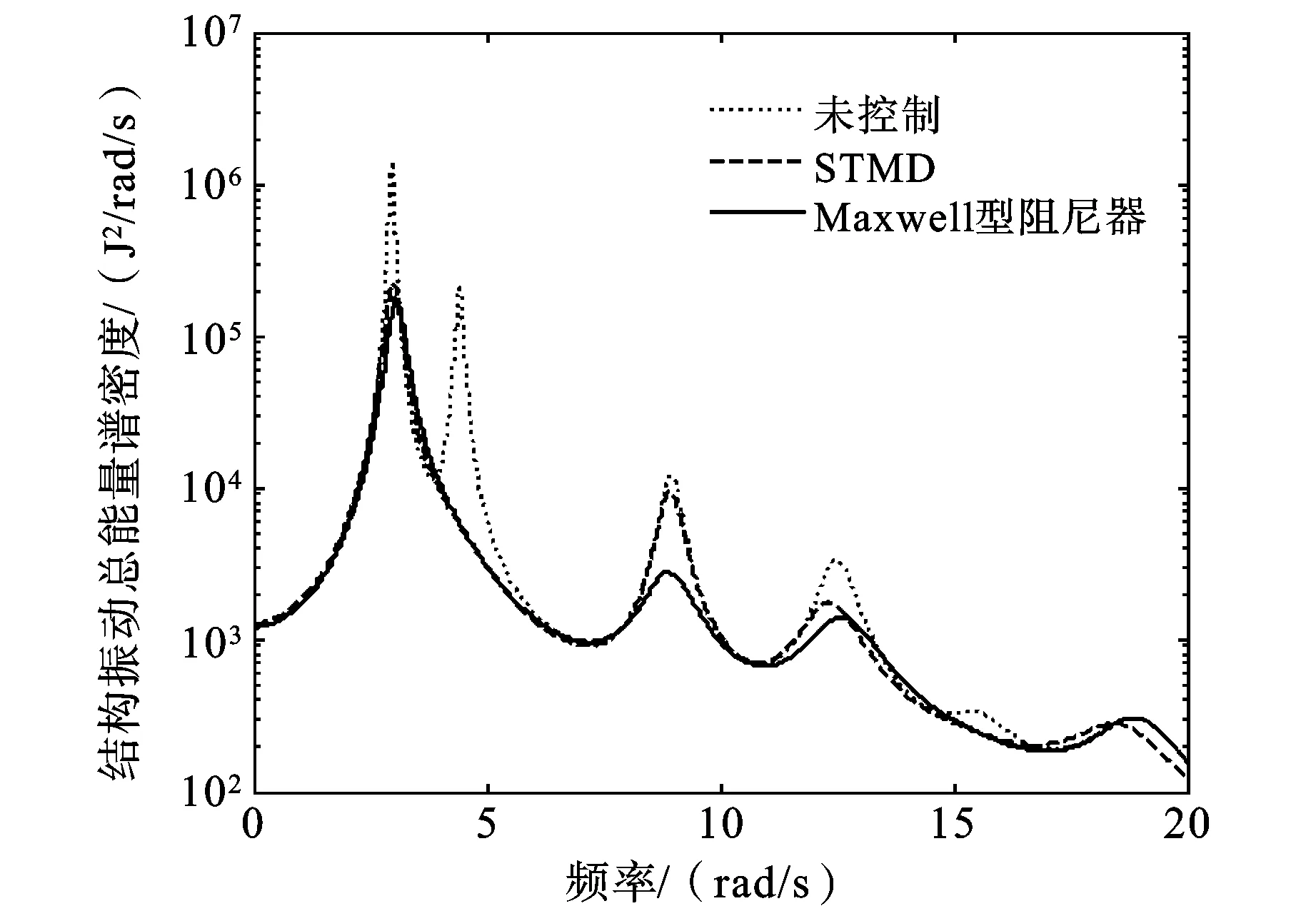
图8 结构振动总能量功率谱密度比较曲线

图9 裙房基底剪力功率谱密度比较曲线

对于控制结构而言，由于耗能减震装置可能会增加结构的刚度和阻尼，导致结构动力特性的改变。如果结构动力特性改变较大，会改变地震作用能量在结构中的分布，甚至导致局部构件的屈服，对结构非常不利，因此需要对设置阻尼器和STMD后结构的动力特性进行评价。经过计算，安装Maxwell型阻尼器后，结构的第一、二阶自振圆频率分别变为3.06和4.35 rad/s，第一、二阶模态阻尼比也从0.02分别增加到0.06和0.29。STMD则使结构第一、二阶自振圆频率分别增至2.99和4.42 rad/s，使结构第一、二阶模态阻尼比分别增至0.06和0.24。可见两种控制方案对结构动力特性影响不大，从结构功率谱密度曲线也可以得到该结论，但结构的模态阻尼比大大增加。

图10与图11分别给出了塔楼1与塔楼2各层层间剪力均方差比较曲线。未控制时，塔楼1底层层间剪力为7.72×106N，设置STMD和Maxwell型阻尼器后，层间剪力分别减小至4.71×106和4.25×106N，减小百分比分别为39%和45%。塔楼2底层剪力未控制时为4.57×106N，设置STMD后为2.91×106N，减小百分比为37%，设置阻尼器后为3.02×106N ，减小百分比为34%。从图中可直接观察到，其他各楼层层间剪力也得到较好的抑制。

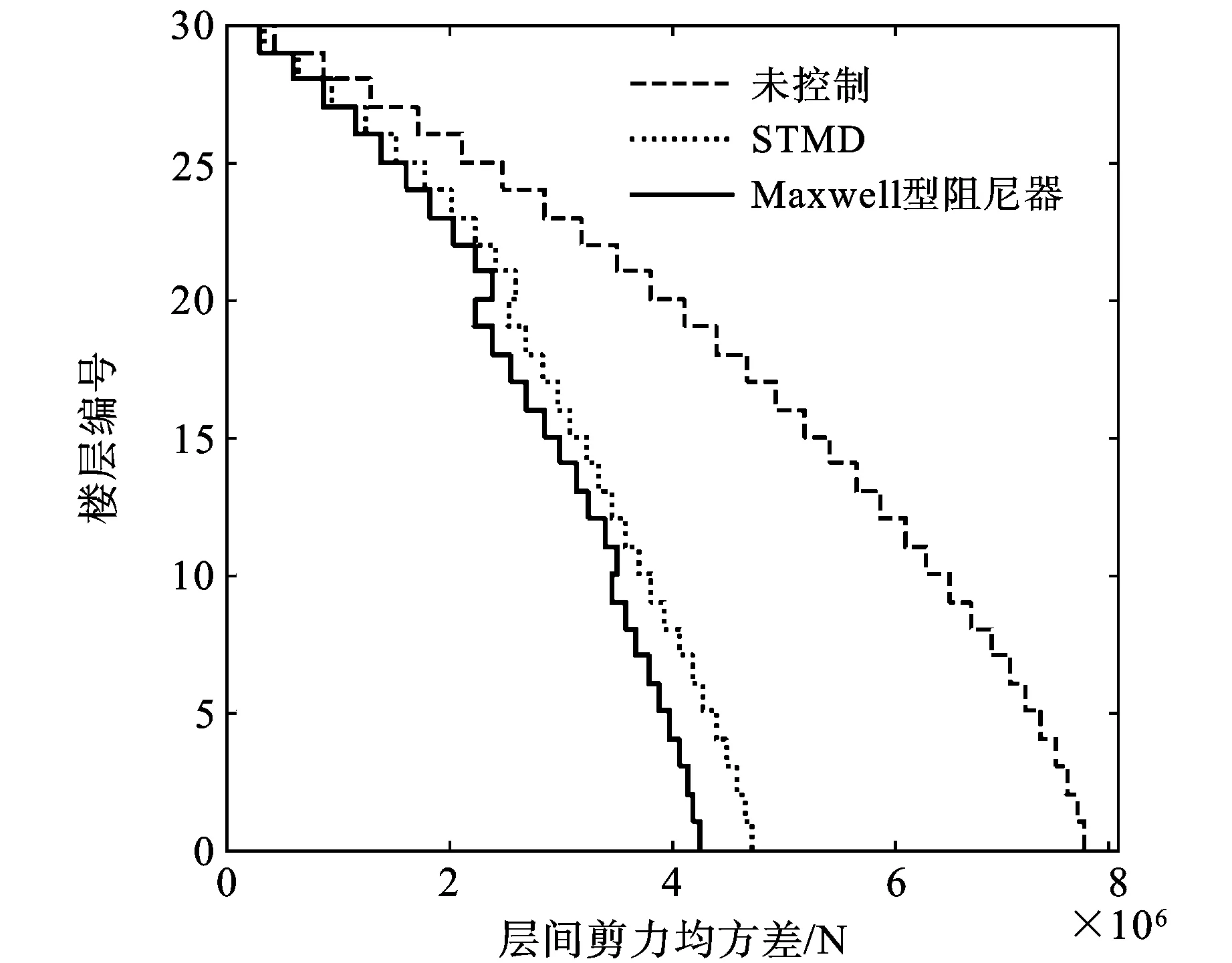
图10 塔楼1各层层间剪力均方差比较曲线

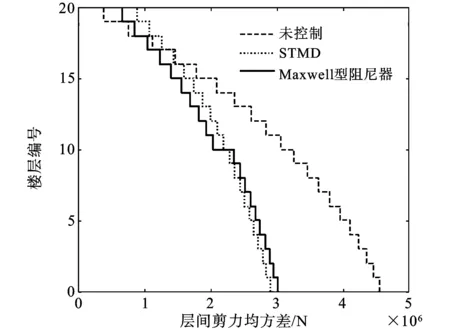
图11 塔楼2各层层间剪力均方差比较曲线

2.4 时域分析结果

为进一步分析STMD和阻尼器连接控制方案在不同地震波激励下的耗能性能，本文共采用三条地震波，分别是1940 El Centro波NS分量、1952 Taft波N21E分量和1995 Kobe波NS分量，加速度调幅为0.2g。

图12与13分别给出了结构相对振动能量和地震输入能量时程曲线，可以看出STMD和阻尼器连接控制方案可大大减小结构振动能量和地震输入能量，Maxwell型阻尼器控制性能略优于STMD。

图12 El Centro波作用下结构振动能量时程曲线

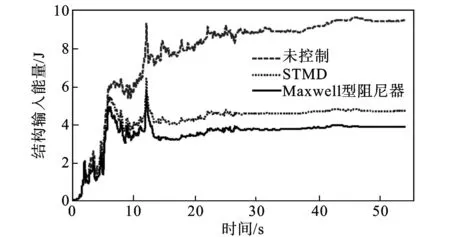
图13 El Centro波作用下结构输入能量时程曲线

表1 Maxwell型阻尼器与STMD控制后结构地震响应均方根减小百分比 (%)

表1中列出了不同地震波作用下，Maxwell型阻尼器与STMD控制后结构地震响应均方根减小百分比。从表中可以发现，塔楼和裙房的地震响应大大减小，各控制方案分别在不同地震波作用下的控制效果不同。Maxwell型阻尼器和STMD在相同地震波作用下的控制性能差别不大，这是因为优化设计时采用了相同的优化目标，使Kanai-Tajimi谱作用下结构总的振动能量最小。

3 结 论

对比以上两种控制方案，虽然二者控制性能差别不太大，但对于不对称的双塔楼结构，阻尼器连接控制方案具有明显的优势，该方案不需要质量块，阻尼器优化参数可直接通过理论公式获得，不需要经过繁琐的参数化研究。STMD方案中，优化设计阻尼系数为8.0×107N·s/m，而连接Maxwell型阻尼器优化设计阻尼系数为2.56×107N·s/m，显然STMD方案比连接阻尼器方案造价更高。更重要的是，STMD依然摆脱不了TMD系统鲁棒性差的特点，频率调谐十分敏感，可控频率仅限于结构第一阶自振频率，不能抑制高阶频率的地震响应。实际上，对于阻尼器连接控制方案，其中的一个塔楼相对于另一个塔楼相当于巨大的TMD，并且具有多个频率，对频率的不敏感性是STMD系统不能相比的。

[1] Zhu H P, Xu Y L. Optimum parameters of Maxwell model-defined dampers used to link adjacent structures [J]. Journal of Sound and Vibration, 2005, 279(2): 253-274.

[2] Zhang W S, Xu Y L. Vibration analysis of two buildings linked by Maxwell model-defined fluid dampers[J]. Journal of Sound and Vibration, 2000, 233(5): 775-796.

[3] Xu Y L, Zhang W S, Ko J M. Experimental investigation of adjacent buildings connected by fluid damper [J]. Earthquake Engineering and Structural Dynamics, 1999, 28(6): 609-631.

[4] Christenson R E, Spencer B F Jr., Johnson E A, et al. Coupled building control considering the effects of building/connector configuration[J]. Journal of Structural Engineering, 2001, 132(6): 853-863.

[5] Christenson R E, Johnson E A. Semiactive connected control method for adjacent multidegree-of-freedom buildings[J]. Journal of Engineering Mechanics,2007, 133(3): 290-298.

[6] Abdullah M M, Hanif J H, Richardson A, et al. Use of a sheared tuned mass damper (STMD) to reduce vibration and pounding in adjacent structures[J]. Earthquake Engineering and Structure Dynamics, 2001, 30(8): 1185-1201.

[7] 閤东东, 朱宏平, 陈晓强. 两相邻结构地震动响应被动优化控制研究[J]. 振动工程学报, 2008, 21(5): 482-487.

[8] Ge D D, Zhu H P, Wang D S, et al. Seismic response analysis of damper-connected adjacent structures with stochastic parameters[J]．Journal of Zhejiang University SCIENCE A, 2006, 11(6): 402-414.

[9] Zhu H P, Xu Y L. Optimum parameters of Maxwell model-defined dampers used to link adjacent structures[J]. Journal of Sound and Vibration, 2005, 279(1-2): 253-274.