GPS定位中的误差分析
2010-01-25康四林李语强
康四林,李语强
(1.中国科学院国家天文台云南天文台,云南 昆明 650011;2.中国科学院研究生院,北京 100049)
GPS(全球定位系统,Global Positioning System)具有高精度、高效率、多功能、多用户、设备轻便、自动化程度高和全天候作业等特点,己经被广泛应用于测量的各个领域,并已发展成为一个真正的三维测量工具。利用GPS定位技术进行定位,存在着多种误差因素。只有深刻理解这些误差的产生原因、性质、大小及其影响,才能采取相应的措施将其减小或消除,从而提高定位精度。
1 GPS的组成
一般将整个GPS系统分为空间部分、地面控制部分和用户部分。
1.1 空间部分
GPS的空间部分由GPS卫星组成。
正式工作的GPS卫星星座于1994年3月完全建成。GPS卫星星座由24颗GPS卫星组成,这些卫星的类型是Block Ⅱ和Block ⅡA,卫星的运行高度为20200km。它们分布在6个倾角为55°的轨道上绕地球运行,轨道偏心率约为0°。卫星轨道运行周期为11h58min,因此,在同一测站上每天出现的卫星分布图相同,只是每天提前约4min。每颗卫星每天约有5小时在地平线上。可以保证在任何时间和任何地点都可以接收到4颗以上GPS卫星发送的信号。每个卫星发射两个频率的信号,L1为1575.42MHz,L2为1227.6MHz,L1载波调制P码和C/A码,L2载波调制P码。P码的码速率为10.23Mb/s,C/A码的码速率为1.023Mb/s,P码的精度比C/A码高,但P码是加密的军用码,C/A码公开。C/A码与P码均调制了50b/s的导航信息。每颗星的导航信息包含有该星的位置、时间、星历等信息。
目前的GPS卫星星座由33颗GPS卫星组成。除使用原有的Block Ⅱ和Block ⅡA卫星外,还包括新发射的Block ⅡR和Block ⅡF卫星。现在新增的GPS卫星是在以前正式开始工作的GPS卫星的基础上改进而形成的。主要的改进是对GPS卫星的信号功率进行了加大,在L2载波上加载了C/A码,并将新的定位信号M码加载在Ll和L2载波信号上,同时加入了频率为1176.45MHz的L5载波,改进了GPS卫星的抗干扰系统,并使卫星的使用寿命有所延长。
1.2 控制部分
GPS的控制部分由GPS卫星跟踪站组成。由于这些跟踪站的作用不同,它们又被分为主控站、注入站、监测站。主控站设在美国本土科罗拉多州斯平士(Colorado.Spings)的联合空间执行中心CSOC(Consolidated Space Operation Center)。注入站分别设在大西洋的阿森松岛(Ascension)、印度洋的狄哥·伽西亚(Diego Garcia)和太平洋的卡瓦加兰(Kwajalein)3个美国空军基地上。早期的GPS地面监测站只有5个。除一个单独设在夏威夷外,其余4个都分设在主控站和注入站上。后增至6个,2005年末,美国国家地理空间情报局(NGA)的6个监测站纳入GPS的卫星地面监测网络,到2006年又增加了5个NGA监测站。这样,GPS的地面监测站数量达到了17个,保证了任意一颗GPS卫星在任何时刻都至少有3个监测站跟踪。
主控站控制和协调各个监测站和注入站的工作,收集各个监测站所测得的伪距和积分多普勒观测值、气象要素、卫星时钟和工作状态的数据、监测站自身的状态数据。主控站根据所收集的数据及时计算出每颗GPS卫星的星历、时钟改正、状态数据以及信号的大气传播改正,并按一定格式编制成导航电文,传送到注入站。当某一颗GPS卫星离分配给它的轨道位置太远时,主控站能够对它进行轨道改正,主控站还能进行卫星调度,让备用卫星去取代失效的工作卫星。主控站肩负监测整个地面控制部分是否正常工作,监测注入给卫星的导航电文是否正确,监测卫星有否将导航电文发送给了用户。各个监测站监测GPS卫星信号,对飞越其上空的GPS卫星进行伪距等测量,并将其测量值发向主控站。注入站将主控站计算出的卫星星历和卫星钟的改正参数等注入到GPS卫星中去,GPS卫星的导航数据,每隔8小时注入一次。
1.3 用户部分
GPS系统的用户部分即GPS信号接收机。GPS信号接收机是实现GPS卫星导航定位的终端仪器。它是一种能够接收、跟踪、变换、处理GPS卫星导航定位信号的无线电接受设备。GPS系统是一种单程系统,用户只接收而不必发射信号,因此用户的数量不受限制。
从GPS信号接收机的结构角度分析,GPS接收机可概括为天线单元和接收单元两大部分。天线单元由接受天线和前置放大器两个部件组成。天线单元的作用是将到达GPS信号接收天线的GPS电磁波变换成微波电信号,并将微弱的GPS电信号予以放大。接收单元由信号波道、存储器、微处理机、频率合成器、显控器、电源等部件组成。信号波道不是一种简单的信号通道,而是一种软硬件相结合的有机体。频率合成器是用一个独立的基准频率源,在压控振荡器的支撑下,运用信号的分频和倍频功能,获得一系列与基准频率稳定度相同的信号输出。
GPS信号接收机有多种分类方法。按测量站星距离所用测距信号的不同,GPS信号接收机可以分为以下3种类型:(1)码接收机:用伪噪声码和载波作测距信号;(2)无码接收机:仅用载波作测距信号;(3)集成接收机:即用GPS信号,又用GLONASS信号测量站星距离。
2 GPS定位原理
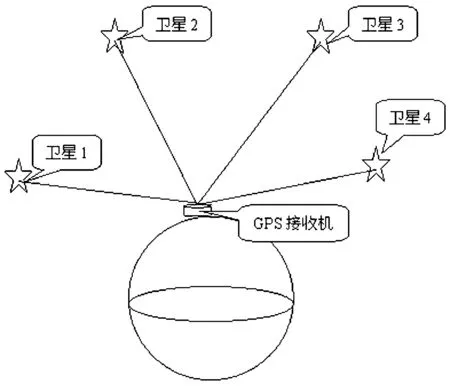
图1 GPS定位原理简图Fig.1 Illustration of the principle of GPS positioning
GPS定位的实质是要确定接收机的三维坐标。GPS信号接收机同时接收到多颗GPS卫星发来的信号,接收机根据卫星发来的导航电文自动选择最佳方位的卫星进行定位。GPS信号接收机测出GPS卫星到接收机的距离。再根据已知的卫星瞬时坐标,利用距离交会定点原理来确定接收机所对应的点位,即观测站的位置。GPS定位须要确定接收机的三维坐标(x,y,z)3个未知数,但因为GPS信号接收机含有接收机钟差这个未知数,因此至少要接收到4颗卫星信号才能定位。其定位原理如图1。
在图1中设GPS信号接收机钟差为δt,c为光速,所使用的卫星1,2,3,4的坐标分别为(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)、(x4,y4,z4),这些卫星到接收机的伪距离分别为P1、P2、P3、P4。要确定GPS信号接收机的位置(x,y,z),只须解下列方程组即可。
[(x-x1)2+(y-y1)2+(z-z1)2]1/2-cδt=P1
[(x-x2)2+(y-y2)2+(z-z2)2]1/2-cδt=P2
[(x-x3)2+(y-y3)2+(z-z3)2]1/2-cδt=P3
[(x-x4)2+(y-y4)2+(z-z4)2]1/2-cδt=P4
(1)
3 GPS定位中的误差分析
GPS卫星导航定位,是基于被动式测距原理。即GPS信号接收机被动地测得GPS接收机天线相位中心和GPS卫星发射天线相位中心之间的距离(即站星距离),进而将它和GPS卫星在轨位置联合解算出GPS接收机的三维坐标。该三维位置误差为:
MP=PDOP×Mρ
(2)
式中PDOP为三维位置几何精度因子;Mρ为站星距离的测量误差。
GPS定位的误差与位置精度因子(PDOP)的大小成正比。位置精度因子的大小与所测卫星的几何分布图形有关。大量分析研究表明,当观测站与4颗观测卫星所构成的六面体体积越大时,所测卫星在空间的分布范围也越大,而这时的PDOP值越小,观测的精度也越好[1]。但是为了降低大气折射对观测精度的影响,通常都要先限制观测卫星的高度角。除此之外,卫星的能见度也是影响观测精度的一个重要方面。一般要求观测站周围屏障物的高度角应小于15°。各种GPS信号接收机都是根据PDOP的算法,计算不同的定位星座的PDOP值的大小,最后选择最佳的定位星座进行跟踪。
站星距离的测量误差同样决定着GPS定位的误差。GPS站星距离的测量误差受多种因素的影响,主要影响因素可以分为3大类:(1)与GPS卫星有关的误差;(2)与GPS信号传播有关的误差;(3)与接收设备有关的误差。
3.1 与GPS卫星有关的误差
与GPS卫星有关的误差主要有星钟误差和星历误差。
3.1.1 星钟误差
尽管GPS卫星均设有高精度的原子钟,但它们与理想的GPS时之间,仍存在着难以避免的频率偏差和频率漂移,也包含钟的随机误差,这种偏差的总量约在1ms以内。由此引起的等效距离可达300m。在GPS测量中,卫星作为高空观测目标,其位置在不断变化,必须有严格的瞬间时刻,卫星位置才有实际意义。另外,GPS测量就是通过接收和处理GPS信号实现定位的,必须准确测定信号传播时间,才能准确测定观测站至卫星的距离。星钟偏差值一般可用二项式来表示[2]:
∂t=α0+α1(t-t0c)+α2(t-t0c)2.
(3)
式中t0c为参考历元;t为需计算卫星钟差的时刻;α0为卫星钟在t0c时刻的钟差;α1为卫星钟在t0c时刻的钟速(频率偏差);α2为卫星钟在t0c时刻的钟速变化率(老化率)。这些参数可从卫星导航电文中获得。用二项式模拟卫星钟的钟差能保证卫星钟与标准GPS时间同步在20ns之内,由此引起的等效距离误差不大于6m。若要进一步削弱卫星钟差,可通过差分定位或者采用IGS产品中的卫星钟差加以实现。
3.1.2 星历误差
卫星星历误差是指由广播星历参数所给出的卫星位置与卫星的实际位置之差。由于卫星在运行中受到多种复杂的摄动力的影响,数个地面监测站难以精确可靠地测定这些作用力,以致难以准确了解他们对卫星的作用规律,使得测定的卫星轨道会有误差。同时,用户得到的卫星星历并非是实时的,这会导致计算卫星位置产生误差。在一个观测时段,卫星星历误差是一种系统性误差,不可能通过多次重复观测来消除,它的存在将严重影响单点定位的精度[3]。减小星历误差的主要方法有:(1)建立独立的GPS卫星观测网进行GPS卫星的精密定位[4],例如IGS观测网络;(2)轨道松弛法。轨道松弛法是在平差模型中把卫星星历给出的卫星轨道视为初始值,将其改正数作为未知数,通过平差求得测站位置及轨道改正数。这种方法数据处理相当复杂,工作量较大,一般只适用于无法获取精密星历而采取的补救措施;(3)差分定位。这一方法是利用在两个或多个观测站上,对同一卫星的同步观测值进行求差。因为星历误差对相距不太远的两个或多个测站的影响相近,所以对于确定两个或多个测站之间的相对位置,可以使用差分定位的方法来减弱卫星星历误差的影响。
3.1.3 IGS产品中的GPS卫星星历和卫星钟差
国际大地测量学协会于1993年成立了国际GPS地球动力学服务(IGS)组织,并于1994年1月正式运作。IGS依靠全球布设的GPS跟踪网,通过所属的7个分析中心各自处理,最后汇集到设在加拿大的IGS协调中心,对分中心的结果进行综合处理,通过加权平均最终得到IGS的综合精密星历及其它信息,并向全球用户提供使用。使用者可以免费从Internet网上(http://igscb.jpl.nasa.gov)取得观测数据及各种IGS产品。目前,IGS组织定期向全球用户提供的IGS产品有:(1)GPS卫星星历。包括超快速星历(IGU星历)、快速星历(IGR星历)和精密星历(IGS星历)。IGU星历文件轨道弧长48小时,前24小时是基于实测GPS数据的精密轨道,后24小时则是预推轨道;(2)GPS卫星和IGS跟踪站钟差信息;(3)IGS跟踪站坐标及其位移;(4)地球自转参数;(5)天顶路径延迟估计。IGS在全球布设的GPS跟踪站接近400个,远远大于GPS系统的地面监测站(17个)的数量。IGS提供的GPS卫星星历和卫星钟差的精度远远高于GPS导航电文所提供的。IGS最新产品中GPS卫星星历和卫星钟差的概况如表1。
从表1可看到,对GPS观测的事后处理,可根据不同的情况用IGS的精密星历和卫星钟差,快速星历和卫星钟差,或超快速星历和卫星钟差(前24小时)来处理,均能获得厘米级的定位精度。对一些精度要求较高(如分米级)的实时(或准实时)定位来说,由于预报的超快速卫星钟差精度较差(达5ns),导致定位精度较低。这时可根据“卫星星历可预报,卫星钟差不可预报”的特性,利用若干站坐标已精密测定的GPS基准站的实时观测资料和超快速的预报星历,来实时(或准实时)计算卫星钟差改正,达到较高精度实时(或准实时)定位的目的。
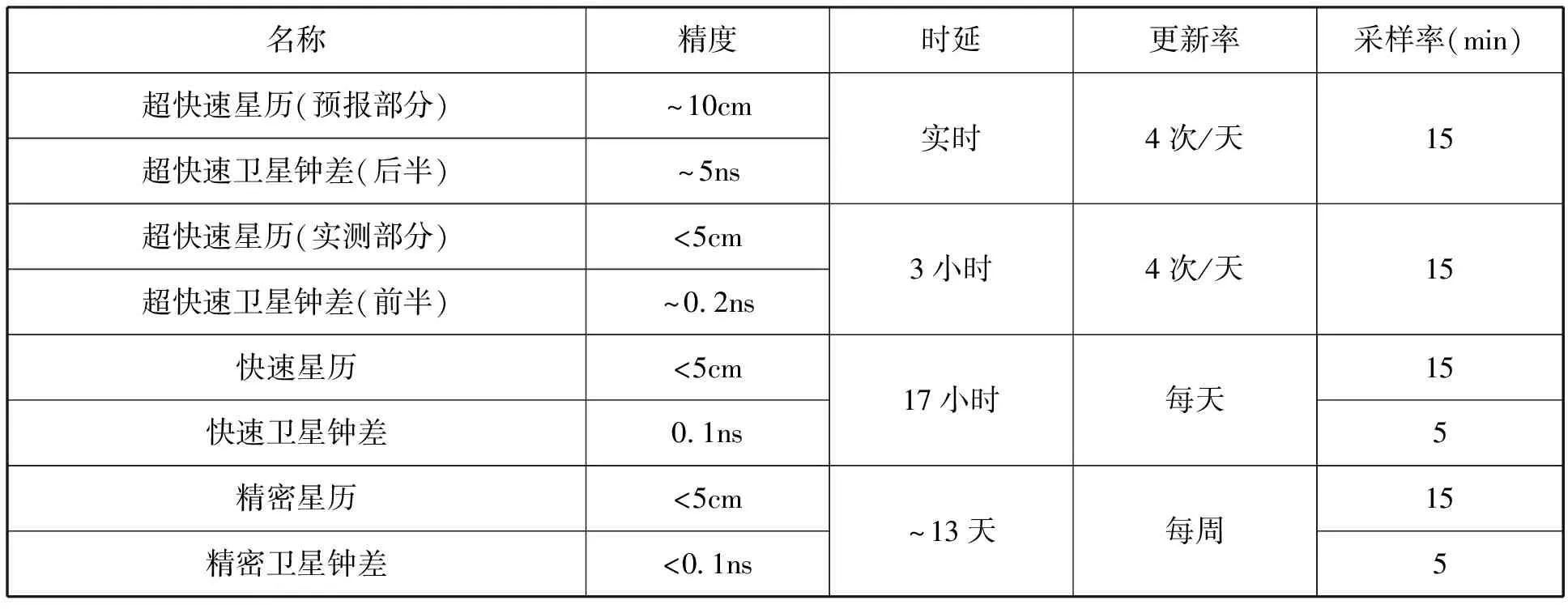
表1 IGS产品表(GPS卫星星历和卫星钟差)
3.2 与GPS信号传播有关的误差
与GPS信号传播有关的误差主要包括电离层折射误差、对流层折射误差、多路径误差、相对论效应误差、地球自转效应误差。
3.2.1 电离层折射误差
电离层是指高度在50~1000km之间的大气层。受太阳辐射的作用,电离层中的中性气体分子被电离而产生大量的正离子和自由电子,从而形成电离气体层。GPS卫星信号和其它电磁波信号一样,当通过电离层时,将产生折射现象,不仅使电磁波信号的传播路径发生变化,而且会引起信号传播速度的变化。电磁波在电离层中的折射率为[5]:
(4)
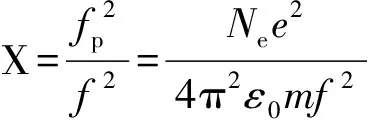
若忽略小于10-9量级的函数项,对GPS信号载波(fL1,fL2,fL5)在电离层中的折射率可以表达为:
(5)
对GPS信号载波而言,高阶电离层效应较小,一般可以忽略。忽略高阶电离层效应的GPS信号载波电离层折射率记作:
(6)
经推导,可得伪距测量的电离层效应的距离偏差改正为:
(7)
载波相位测量的电离层效应的距离偏差改正为:
(8)
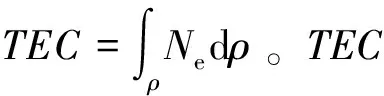
减弱或消除电离层影响的有效措施通常有以下几种:(1)采用双频接收技术。由(7)、(8)式可以看出电离层的影响是电磁波频率的函数。如果分别用两个频率f1和f2发射卫星信号,则两个不同频率的信号就会沿同一路径到达接收机,用双频接收机进行测量,就能根据电离层折射和信号频率的有关特性,求得电离层折射改正数。但是在太阳磁暴和耀斑爆发及太阳黑子活动的异常期,应避免观测[6]。由于赤道和地极附近存在着严重的电离层赤道扰动和地极扰动[7],因而在赤道和地极附近一般不利用双频GPS接收机观测。双频GPS接收机一般只适用于没有电离层扰动的中纬度地区来进行电离层改正。(2)利用电离层改正模型[8]。对于GPS单频接收机,一般采用导航电文中提供的电离层延迟改正模型或其它较高精度的电离层延迟改正模型,来减弱电离层的影响。由于决定电离层折射的因素很多,所以,难以建立严格的改正模型。(3)差分处理。当测站间的距离相距不太远时(例如20km以内),两测站上的电子密度相差不大,卫星的高度角相差不多,此时卫星信号到达不同观测站所经过的介质状况相似、路径相似,当利用两台或多台接收机对同一组卫星的同步观测值求差时,可以有效地减弱电离层折射的影响。
3.2.2 对流层折射误差
对流层是离地面高度约为50km以下的大气层。GPS信号通过对流层时将产生折射,从而引起信号传播延迟[9]。电磁波在对流层的传播速度与电磁波的频率无关,只与电磁波的传播方向和大气折射率有关[10]。对流层大气折射率与大气压力、温度和湿度有关,一般将对流层中大气折射率N0分为干分量Nd和湿分量Nw两部分。
N0=Nd+Nw
(9)

(10)
式中p为大气压力(mbar);TK为绝对温度(TK=T0+273.16);e0为水汽分压(mbar)。
对流层折射对电磁波信号所引起的路径延迟为:
δρtrop=ρd+ρw
(11)
上式中ρd为干分量;ρw为湿分量。对于ρd和ρw的霍普菲尔德(Hopfield)对流层估计模型为:
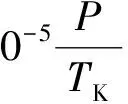
(12)
式中HT为测站高程(m);Hw为湿分量高程平均值(m);α为电磁波传播方向的高度角。
减弱对流层折射的影响,一般有以下几种措施:(1)利用水气辐射计直接测定信号传播的影响。(2)用改正模型进行对流层改正。常用的各种改正模型是利用气象参数进行计算改正。其气象参数在测站直接测定。用改正模型进行对流层改正,其所用设备简单,操作方法易行。但是由于水汽在空间的分布很不均匀,不同时间﹑不同地点水汽含量相差甚远,用统一模型难以准确描述,所以,对流层改正的湿分量部分精度较低,只能将湿分量消去80%~90%。(3)差分处理。与电离层折射的影响类型类似,当两观测站相距不太远时(例如20km以内),由于GPS卫星信号通过对流层的路径大体相近,相近路径的气象参数相近,所以,对同一卫星的同步观测值进行求差,可以明显减弱对流层折射的影响。
3.2.3 多路径误差
GPS卫星信号从20200km高空向地面发射,经接收机周围某些物体表面反射后到达的信号与直接来自卫星的信号叠加进入接收机,使观测值偏离真值,这就是所谓的多路径误差。多路径的信号传播所引起的干涉时延效应被称作多路径效应。多路径误差与反射物的反射系数有关,也与反射物离测站的距离及GPS卫星信号方向有关,无法建立准确的误差改正模型[11]。减小多路径误差的方法主要有以下几种:(1)选择较好的测站环境,避免有高反射系数的反射面,如水面、光滑的地面及高层建筑物等;(2)尽量选择能抑制多路径效应的天线,如带抑制板或抑制圈的天线;(3)由于多路径误差分为常数部分和周期性部分,因此可以通过增加观测时间来消除周期性部分;(4)用小波对观测数据进行滤波,分离有用信号,实现消除噪声的目的[12]。
3.2.4 相对论效应误差
由于爱因斯坦的狭义相对论和广义相对论效应的影响,卫星钟频率与地面静止钟频率相比,发生频率偏移,这种频移带来的误差在精密定位中是不可忽略的。
按照狭义相对论的观点,在惯性参考系中,一个静止频率为f0的时钟安装在飞行速度为υ的卫星上,相对静止不动的同类时钟来说其频率将产生变化,其改变量为:
(13)
地面钟随地球一起以速度VR自传时,也会产生狭义相对论效应。此时地面钟相对静止不动的同类时钟来说其频率也将产生变化,其改变量为:
(14)
由于△fR的量非常小,所以计算VR时可以把地球看成是半径为Rm的圆球,有:
VR=V0cosφ
(15)
上式中V0为地球赤道处的自传速度,其值为464m/s。在GPS测量中,测定的是卫星信号的传播时间(t2-t1)。其中t1是用卫星钟测定的信号离开卫星的时刻;t2是用接收机钟测定的信号到达接收机的时刻。在讨论狭义相对论效应的影响时,理应同时考虑狭义相对论效应对卫星钟的影响以及对接收机钟的影响,但通过计算(14)式可知,接收机钟所受到的狭义相对论效应的影响很小,通过(13)式和(14)式的对比,可以发现对于大多数地面测站来说,狭义相对论效应对地面钟的频率改变量不足狭义相对论效应对卫星钟的频率改变量的1%。而且,狭义相对论效应对地面钟的频率改变很难与真正的接收机时钟误差分离开来,也就是说,在GPS测量中狭义相对论效应对接收机时钟的影响会自动地被吸收到接收机时钟的误差项中去。
由以上讨论可知,卫星钟比静止在地球上的同类钟走慢了。根据公式:
(16)
可得:
(17)
按照广义相对论的观点,处于不同等位面的时钟,其频率f0将由于引力位不同而发生变化。卫星钟与地面钟相比处于较高的引力位,将产生引力频移,此时卫星钟要走得快一些,其钟频增加量为:
(18)
由(17)、(18)式可知,对GPS卫星来说,广义相对论效应的影响大于狭义相对论效应的影响,且符号相反,相对论效应的综合影响为:
(19)
上述各式中c为真空中光速;g为地面重力加速度;Rm为地球平均半径;Rs为卫星轨道平均半径。
将GPS卫星钟的标准频率f0=10.23MHz代入上式得△f=0.00455Hz。这说明卫星钟比地面钟走得快。为了补偿相对论效应的影响,需将GPS卫星钟的频率减小约0.00455Hz。使卫星钟进入轨道受到相对论效应影响后,恰与标准频率10.23MHz相一致。
上述讨论,是基于GPS卫星做严格的圆周运动。事际上,GPS卫星轨道是一个椭圆,而椭圆轨道各点处的运行速度是不相同的,相对论效应频率补偿,就不是一个常数。频率常数补偿所导致的补偿残差称为相对论效应误差。相对论效应误差所引入的GPS信号时延为[5]:
Δt(ns)=-2289.7esinE
(20)
上式中e为GPS卫星椭圆轨道的偏心率,E为GPS卫星的偏近点角。当e=0.01,E=90°时,相对论效应误差导致的时延达到最大值,即为22.869ns,这相当于6.864m的站星距离的误差,而必须予以考虑。
3.2.5 地球自转效应误差
GPS信号从20200km的高空传播到GPS信号接收机,需要0.067s左右的时间。由于地球的自传(地面测站相对于地心的运行速度约为0.46km/s),GPS信号到达GPS接收机时的GPS卫星在轨位置,不同于GPS信号从卫星发送时的GPS卫星在轨位置,两着之差为:
(21)
式中的ωe是地球自转角速度,且ωe=7.292115×10-5rad/s。上述位置偏差导致的站星距离变化值为[5]:
(22)
3.3 与接收设备有关的误差
与接收设备有关的误差主要包括观测噪声误差、内时延误差和天线相位中心误差。
3.3.1 观测噪声误差
观测噪声,主要源于天线噪声和环路噪声。天线噪声是由客体噪声和背景噪声组成的,客体噪声是因各种电机的火花放电,以及电台、电视和雷达的高频射电而致。背景噪声,不仅包括因雷电和大气涨落引起的天电干扰噪声,而且包括银河噪声和太阳噪声。到达GPS信号接收天线的GPS信号弱达3.5E-16W,它极易受到天线噪声的干扰。GPS信号接收机的伪噪声码跟踪环路和载波跟踪环路等电路,因信号电流在其内的流通和变换,而产生热噪声和磁起伏噪声。观测噪声对观测成果的精度损失,取决于观测噪声功率相对于GPS信号功率的大小。
3.3.2 内时延误差
GPS信号接收机是用于接收、跟踪、变换和测量GPS信号的。GPS信号在接收机内部从一个电路转移到另一个电路的进程中,必定会占用一定的时间。这种由于电子电路所产生的时间延迟,称为内部时延。它的大小可以根据电路参数计算求得。如果内时延是稳定不变的,经过内时延改正后的站星距离,不存在测量精度的损失。但是,由于波道时延的不稳定性,中频信号的相位抖动和接收天线的相位中心漂移,不可能实现接收机内时延的精确改正。例如,对于多波道接收机而言,因各个波道不可能产生相同的波道时延,而存在波道时延偏差。制作GPS信号接收机时,虽给予了时延补偿,且设有内时延自动校正程序,在数据文件中还能够读取各个波道的相对时延值。但是,因内时延的不稳定性,仍旧存在着自校残差。
3.3.3 天线的相位中心误差
在GPS测量中,观测值都是以接收机天线的相位中心位置为准的,所以,接收机天线的相位中心应该与其几何中心保持一致。但实际上天线的相位中心位置随信号输入的强度和方向不同会发生变化,使其偏离几何中心。这种偏差视天线性能的好坏可达数毫米至数厘米,这对精密定位来说,是不容忽视的。实际工作中如果使用同一类型天线,在相距不远的两个或多个测站同步观测同一组卫星,可以通过观测值求差来减弱相位中心偏移的影响。
4 结 论
GPS定位精度的高低,与所选用的GPS信号接收机及所采用的定位方法有着密切的关系。如果对定位精度要求不太高,比如普通的民用,可以选用普通的接收机,采用较简单的误差改正模型,使用单点定位方法进行定位。这样既可以节约定位成本又可以提高定位效率。但有些定位必须要求高精度,比如军用及相关科学研究,在这种情况下,必须选用接收性能良好的接收机。同时也要采用最精确的误差改正模型或者差分定位方法来减小或者消除误差。例如,采用双频载波相位双差技术。双频载波相位双差技术可以抵消大气折射、钟差、相对论效应、星历误差、岁差、章动、极移、地球固体潮等诸多共性观测因素导致的误差。
[1] 张清志,陈智粱,刘宇平.GPS测量误差分析[J].沉积与特提斯地质,2002,22(3):100-106.
ZHANG Qing-zhi,CHEN Zhi-liang,LIU Yu-ping.The error analysis in GPS measurements [J]. Sedimentary Geology and Tethyan Geology,2002,22(3):100-106.
[2] 王晓华,郭敏.GPS卫星定位误差分析[J].全球定位系统,2005,1:43-47.
WANG Xiao-hua,GUO Min.Discussing error theory on GPS secondary planet orientation[J].GNSS World of China,2005,1:43-47.
[3] Lachapelle G,Cannon M E.Precise aircraft single-point positioning using GPS post-mission orbits and satellite clock corrections[J].Journal of Geodesy, 1996,70(9):562-571.
[4] Kouba J.Precise Point Positioning Using IGS Orbit and Clock Products[J].GPS Solutions, 2001,5(2):12-28.
[5] 刘基余.GPS卫星导航定位原理与方法[M].北京:科学出版社出版,2003.
[6] 谢世杰,韩明锋.论电离层对GPS定位的影响[J].测绘工程,2000,9(1):9-15.
XIE Shi-jie,HAN Ming-feng.On Effects of Ionosphere on GPS Positioning[J].ENGINEERING OF SURVEYING AND MAPPING,2000,9(1):9-15.
[7] 贾彬.GPS测量误差源及其控制分析[J].海洋测绘,2008,28(3):76-78.
JIA Bin.Source Controlling Analysis of Errors in GPS Surveying[J].HYDROGRAPHIC SURVEYING AND CHARTING,2008,28(3):76-78.
[8] Yang Gao,Zhi zhao Liu.Precise ionosphere modeling using regional GPS network data[J].Journal of Global Positioning Systems, 2002,1(1):21-24.
[9] F K Brunner.Effect of the troposphere on GPS measurements[J].GPS World,1993,4(1):42-51.
[10] Scbenewerk M,Dam van,Sasagawa T M.A detailed analysis of tropospheric effects on geodetic observations[J].Phys Chem Earth,1998,(23):103-106.
[11] Zhang Yong-jun,Wang Ze-min.Analyses and solutions of errors on GPS/GLONASS positioning[J].Geo-Spatial Information Science,2002,5(2):6-12.
[12] 罗兆文,王文,王玉宏.基于小波变换的GPS载波相位测量误差分析[J].全球定位系统,2007,1:26-31.
LUO Zhao-wen,WANG Wen,WANG Yu-hong.Carrier Phase Dual Differential GPS Measurement Error Analysis Based on Wavelet Analysis[J].GNSS World of China,2007,1:26-31.