超磁致伸缩驱动器二维轴对称非线性驱动位移模型及有限元分析*
2010-01-25谭先涛杨斌堂徐彭有杨德华
谭先涛,杨斌堂,孟 光,徐彭有,杨德华
(1. 上海交通大学机械系统与振动国家重点实验室,上海 200240;2.中国科学院国家天文台南京天文光学技术研究所,南京 210042)
由于大口径镜面制造困难,目前世界上的大口径天文光学望远镜方案均采用了拼接子镜主动光学技术,采用六面体或者扇形子镜拼接而成,并通过单个镜面的精密控制来实现整体镜面的协调一致。控制单个镜面的微位移驱动器需要具有高精度、大行程以及大负载的技术要求。目前广泛使用的微位移驱动包括电机驱动、液压驱动、压电驱动等驱动方式。电机驱动的机械式微位移驱动器存在着间隙、传动误差、摩擦损耗及爬行等现象,难以到达高精度的要求;液压驱动的微位移驱动器分辨率较低、输出负载能力较小、反应速度较慢;压电驱动器具有高分辨率大承载等优点,但由于压电应变量较小,难以实现大行程,并且需要高电压驱动,发热严重。超磁致伸缩驱动器(Giant Magnetostrictive Actuator,GMA)具有输出位移和输出力大、机械响应速度快等优点,在大型天文望远镜拼接子镜的精密驱动控制方面具有潜在优势。
GMA的核心部件为超磁致伸缩材料(Terfenol-D)棒。Terfenol-D作为一种稀土超磁致伸缩材料,具有非常复杂的电磁-结构-热多物理场耦合特性,并且其材料属性如相对磁导率、弹性模量等随外加磁场、预压应力以及温度的变化而变化。建立精确的数学模型,并选用有限元计算方法对GMA进行仿真分析,从而优化GMA的结构和电磁性能,对提高GMA的输出性能具有重要意义。
针对GMA的研究,Engdahl、Perez和Kannan[1-3]分别建立了描述其耦合特性的模型,但是都没有考虑到材料属性参数的非线性变化;Benatar[4]采用FEMLAB计算了耦合三维有限元模型,但也没有考虑参数的非线性;赵章荣[5]引入Jiles-Atherton磁滞模型建立了三维动态有限元模型,但由于模型的强非线性,三维模型计算复杂,不易得到收敛结果。基于以上分析,并结合所设计驱动器实际工作环境,本研究采用Jiles-Atherton模型计算磁化强度M、磁致伸缩量λ和磁场强度H、预压应力σ0之间的非线性关系,建立了二维轴对称非线性有限元模型,并尝试使用商用有限元软件COMSOL 3.5实现了整个驱动器的电磁-结构全耦合分析。
1 超磁致伸缩驱动器二维轴对称非线性位移模型
直动型超磁致伸缩驱动器的工作原理是由励磁线圈通入电流产生电磁场,超磁致伸缩棒(Terfenol-D)在磁场作用下,由于内部磁畴的偏转而产生伸缩变化,并由输出顶杆输出位移和力,驱动负载。
基于驱动器的轴对称性质,采用二维轴对称方式建立驱动器建立有限元模型,不仅可以保证求解的精度不下降,同时可以大大节省计算机资源。如图1,为超磁致伸缩驱动器的结构模型。

图1 GMA结构示意图Fig.1 Structure of a giant magnetostrictive actuator(GMA)

图2 超磁致伸缩驱动器电磁场和机械应力场耦合关系Fig.2 Illustration of the couplings between electromagnetic field and mechanical stress field in a GMA
如图2,驱动器中包含电磁—机械的双向耦合。利用有限元方法分析超磁致伸缩驱动器的性能,实际上就是求解描述耦合物理场偏微分方程边值问题。以下过程将首先建立电磁场和机械应力场的偏微分方程及其边界条件,然后引入Jiles-Atherton模型描述Terfenol-D棒内的电磁—机械耦合特性。
1.1 超磁致伸缩驱动器的电磁场
驱动器工作在电磁场中,采用Maxwell方程组描述电磁场特性[6]:

(1)
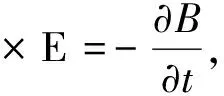
(2)
▽·D=ρ,
(3)
▽·B=0,
(4)

针对驱动器的轴对称特性,使用磁矢量势描述电磁场,则只有圆周方向分量Aφ≠0。
根据(1)可知:

(5)
对上式两边同时乘以δAφ(δAφ表示Aφ的变分),并在整个域内积分,可得积分弱解形式方程为:
▽×δAφ)tHdΩ+

(6)
电磁场方程求解的初始和边界条件为:
A|t=0=A0, ∂ΩA∶A=A*
A|t=0=V0, ∂ΩV∶V=V*
(7)
1.2 超磁致伸缩驱动器的机械应力场
根据牛顿第二定律,Terfenol-D棒内部力平衡方程为:

(8)
其中T为应力;b为体积力;u=[u,w]T;u、w分别表示径向和轴向的位移。
应力-应变关系根据胡克定律有:
T=CS
(9)
其中C为刚度矩阵;S为应变向量。应变-位移关系为:
(10)
对式(8)两端同时乘以δu,并在整个域内积分,可得积分弱解形式方程:
(11)
应力张量T由3部分组成[2]:机械应力分量Tmech;Maxwell应力张量Tm;预压应力张量T0。其中:

(12)
机械应力场方程求解的初始和边界条件为:
(13)
1.3 GMM内的磁-结构耦合场
GMM中磁场H由线圈的源磁场Hs以及磁化产生的磁场HM组成[7]:
H=Hs+HM
(14)
式中HM=-▽φ,φ表示简化磁标量位,则GMM中的磁场强度可表示为:
H=-▽φ+Hs
(15)
A E Clark在1980年提出了描述超磁致伸缩效应的线性压磁方程:
S=T/YH+dH,
(16)
B=dT+μTH.
(17)
其中YH、d和μT分别表示Terfenol-D棒的弹性模量矩阵、压磁系数矩阵和磁导率矩阵;上标H,T分别表示恒定磁场和恒定应力条件。
线性压磁方程是在一定的外加偏置磁场和预压力作用下,忽略磁滞非线性特性的基础上得到的,能够描述磁致伸缩和逆磁致伸缩效应,但不能反映材料的磁滞回特性。
Jiles和Atherton建立了J-A磁滞模型[8-9],该模型基于微磁学理论和Weiss磁筹理论,表达式简单,参数较少。本文采用J-A模型描述Terfenol-D棒的磁化过程。包含外加可变预应力σ0的J-A模型表达式为:
(18)


表1 预压应力为8MPa,最大电流为8A时通过遗传算法辨识出的J-A模型参数
压磁方程中,总的应变是由弹性应变T/YH和磁致伸缩应变dH两部分构成。磁致伸缩应变λ=dH根据二次畴转模型可写为:
(19)
式中M可以通过J-A模型,采用四阶Runge-Kutta法计算求得。计算得到的M-H,λ-H,曲线如图3。

图3 根据Jiles-Atherton磁滞模型计算得到的磁化强度、磁致伸缩量和磁场强度的函数关系Fig.3 The variations of magnetization and magnetostriction displacement with magnetic field intensity according to the Jiles-Atherton model
将上述获得的M-H、λ-H关系写成代数插值表达式,带入(16)中可以得:
T=EHS-EHλ
(20)
磁致伸缩棒内的磁感应强度B可以通过B、H、M之间的关系获得:
B=μ0(M+H)
(21)
(20)、(21)即为包含磁滞的非线性本构关系。
根据以上分析,(6)、(11)分别为电磁场和机械应力场的控制方程;(7)、(13)分别为两个物理场的边界条件。同时考虑(20)、(21)的本构方程式,采用有限元方法进行求解。
2 COMSOL Multiphysics 3.5求解及实验结果比较
COMSOL Multiphysics是一款大型的高级数值仿真软件。它基于偏微分方程组定义物理模型,具有很好的交互开发环境界面。COMSOL Multiphysics成功实现了任意多物理场、直接、双向实时耦合。既可以直接选择封装的模块来模拟某一类型的物理模型,也可以采用PDE(Partial Differential Equations)模块来直接定义特殊的物理模型。基于超磁致伸缩材料独特的磁-结构非线性耦合特性,在比较了常用的数值仿真软件如ANSYS之后,最终选用了COMSOL Multiphysics 3.5作为解决超磁致伸缩材料非线性多物理场耦合问题的计算分析平台。
在COMSOL Multiphysics3.5中,首先选择模型的空间维度为2D轴对称,然后设置3个物理环境:2D轴对称应力-应变模型,变量{uor,w,p};2D轴对称磁场模型,变量{Aphi};2D弱解模型,变量{u1,w1,Vm}。输入几何模型之后,即可以设置参数、表达式、函数来定义物理环境常量及变量(材料参数、求解域参数、边界设定等)。对于应力-应变模型和磁场模型,可以直接设置这些参数,而对于弱解模型,自定义的弱解表达式如表2。

表2 自定义的弱解形式方程式
其中,sr、sz、er、ez分别表示径向和轴向的应力、应变;Br、Bz、Hr、Hz分别表示径向和轴向的磁通量密度和磁场强度;rho_rod表示超磁致伸缩棒的密度;_w,_test分别表示弱解模式的名称和试探函数。电磁场和应力场相互联系的本构关系通过设置等式表达式的变量来实现。
如前所述,选择了实验最佳预压应力σ0=8MPa,激励源为一个760匝,线径为1mm的铜线圈,电流施加方式为随时间斜线增大到8A。
基于以上分析,对GMA进行全耦合计算,计算结果如图4~6。由图4、5可以看出,在电流强度为8A情况下,超磁致伸缩棒内部磁场强度大约为60KA/m,应变大约为1250ppm,并且在磁致伸缩棒两端的应变要大于棒中间的应变,这主要是由于磁致伸缩棒两端的磁场强度要略大于中心位置的磁场强度。
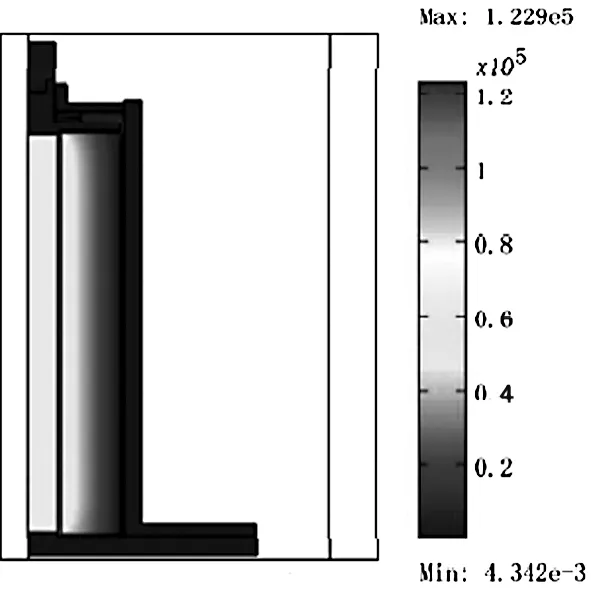
图4 超磁致伸缩驱动器磁场强度分布计算结果Fig.4 Calculation result of the magnetic field intensity distribution in the GMA
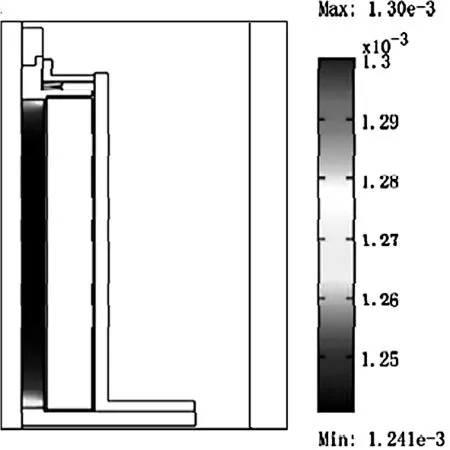
图5 磁致伸缩棒内部应变分布计算结果Fig.5 Calculation result of the strain distribution in the GMM rod
分别选取磁致伸缩棒几何中心点和驱动器输出端面中点,通过COMSOL Multiphysics 3.5计算整个时间历程的磁致伸缩棒内的磁场强度和驱动器的位移量,计算结果和实验结果的对比如图6。

图6 (a)激励磁场强度和输入电流强度之间的关系;(b)输出位移和输入电流强度之间的关系Fig.6 (a)Relation between excitation magnetic field intensity and input electric current; (b)Relation between output displacement and input electric current
由于所设计的超磁致伸缩驱动器工作在准静态环境中,在此没有考虑涡流损耗,所以电流强度和磁场强度呈线性关系;输出位移量和试验值具有相同的变化趋势,最大误差不大于10%。
3 结 论
本文根据Jiles-Atherton磁滞模型、二次畴转模型以及应力-应变模型建立了不考虑涡流损耗的超磁致伸缩驱动器的二维轴对称非线性有限元模型。通过分别建立机械应力场,电磁场的积分弱解方程,并采用Jiles-Atherton模型来描述两场之间的耦合关系,在COMSOL Multiphysics 3.5 软件中进行求解计算,得到的驱动器输出位移和实验数据进行了对比,发现误差较小,说明了该方法的正确性和实用性。由于驱动电流的频率变化对驱动器的输出特性有巨大的影响,下一步的工作是研究在计及涡流损耗的情况下,驱动电流的频率变化对输出特性的影响。
[1]Engdahl G,Svensson L. Simulation of the magnetostrictive performance of Terfenol-D in mechanical devices[J].Appl Phys,1988,63(8):3924-3926.
[2]J L Perez-Aparicio,H Sosa. A continuum three-dimensional,fully coupled,dynamic,non-linear finite element formulation for magnetostrictive materials[J].Smart Material and Structure,2004,13(3):493-502.
[3]Kannan Kidambi Srinivasan.Galerkin Finite Element Scheme for Magnetostrictive Structures and Composites[M].Department of Mechanical Engineering, University of Maryland,1997.
[4]Benatar J G,Flatau A B.FEM implementation of a magnetostrictive transducer[J].Smart Structures and Materials,Proceedings of SPIE,2005,5764:482-493.
[5]赵章荣,邬义杰,顾建新,等.超磁致伸缩执行器的三维非线性动态有限元模型[J].浙江大学学报(工学版),2008,42(2):204-208.
Zhao Zhangrong, Wu Yijie,Gu Jianxin,et al.Three-dimensional nonlinear dynamic finite element model for giant magnetostrictive actuators[J].Journal of Zhejiang University(Engineering Science),2008,42(2):204-208.
[6]赵凯华,陈熙谋.电磁学下册[M].高等教育出版社,1985,6:793-795.
[7]MAGSOFT Corporation.ATILA Finite Element Analysis for Piezoelectric and Magnetostrictive Structures.User’s Manual,2003,34.
[8]Jiles D C,Atherton D L.Theory of ferromagnetic hysteresis[J].Journal of Magnetism and Magnetic Materials,1986,61(1-2):48-60.
[9]Jiles D C,Atherton D L.Theory of the magnetization process in ferromagnets and its application to the magnetomechanical effect[J].Phys D:Appl Phys,1984,17(6):1265-1281.
