引力常数随时间变化对双星(密近食双星)轨道演变的影响(圆形轨道情形)*
2010-01-25李林森
李林森
(东北师范大学物理学院,长春 130024)
自从狄拉克(Dirac)(1937)[1-2]提出了引力常数随时间变化后,这种理论在天文学和地球物理学领域显示很大影响。首先,Kholchenikov和Fracassini(1968)[3]根据狄拉克的大数假说研究了具有引力常数变化的二体问题。他们将理论应用于行星经度变化的估计。Hut和Verhulst(1976)[4]研究了引力常数随时间减少的二体问题,并推出了平均运动和平均经度的长期变化的方程式,给出了真经度的性质[4]。同年,Bishop和Landsberg(1976)[5]从能量守恒定律推出了具有引力常数随时间变化的牛顿引力定律的运动方程公式。随后Maite(1978)[6]利用此理论研究在圆形轨道中引力常数随时间变化和地球表面的有效温度之间的关系,但他没有研究引力常数变化和圆形轨道演变之间的关系。本文在这方面做了研究。一般来说,食双星轨道并非都为圆形轨道或轨道偏心率为零,但有些密近食双星的轨道为圆形轨道,所以本文的理论结果适用于密近食双星轨道的演变。
1 引力常数随时间变化产生的轨道根数变化(圆形轨道情形)
Maiti(1978)根据Bishop和Landsberg(1976)给出的公式推出了具有引力常数随时间变化的矢量运动方程[5]:

(1)


(2)
其中r为圆轨道半径;n为平均运动(轨道平均角速度)。 将(1)式写成标量方程:
(3)
(4)
将G(t)展开为Taylor级数:
(5)
其中G(t0)=G0为牛顿引力常数(不随时间变化)。

(6)
(7)
将方程(6)~(7)同牛顿运动方程相比较后可得后牛顿项:
(8)
(9)
因此后牛顿摄动加速度的径向和切向分量是:
(10)
(11)
(δFr)PN和(δFθ)PN可以认为具有引力常数G0的牛顿运动方程的改正项或为变引力常数G(t)的摄动项。因此,S和T就是具有G0的高斯摄动方程的摄动加速度。 利用以时间为自变量的高斯方程[7]:
其中a为轨道半长轴;e为轨道偏心率;E为偏近点角;p=a(1-e2)。
本文研究圆形轨道情形。对于圆形轨道:a=r(圆轨道半径);e=0;E=θ=nt;p=r。将这些代入轨道半长径和轨道偏心率随时间变化的高斯摄动方程[7],得:
(12)
(13)
将(10)~(11)的S和T代入(12)~(13)式,得:
(14)
(15)
(16)
再推出轨道周期P的变化。将n=2π/P代入Kepler第三定律并对时间微分,得:
将(14)代入上方程,积分上述方程,可得:
(17)
下面推出轨道偏心率的变化。积分方程(15)后,可得到轨道偏心率e的变化:
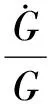
(18)
结果表示:轨道半径和周期以线性形式随时间而缩减,圆形轨道的形状以周期和混合长期项随时间而变化。
2 对5个密近食双星轨道半径和轨道周期的长期演变的上下限估计
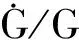


表1 5个密近食双星轨道半径和轨道周期长期演变的上下限估计
3 讨论和结论
(1) 由(16)式和(17)式可知,轨道半径和轨道周期以线性形式随时间缩小。
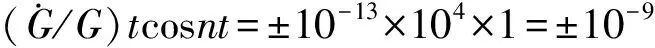

(4) 因二体问题在共面上运动,垂直轨道平面的摄动加速度分量W=0,将其代入摄动方程后轨道倾角的i和升变点经度Ω不变。
(5) 同其他4种效应相比较。如果将e=0(圆轨道情形)代入作者在文[10-13]中椭圆轨道情形中的双星多方模型摄动效应、后牛顿效应、二体自转效应和引力辐射阻尼效应的式子,可得引力常数变化对圆形轨道半径和轨道偏心率的效应同另外4种效应的对比如表2。

表2 在圆形轨道情形中引力常数变化对轨道半径和轨道偏心率产生的效应和其他4种效应的对比
由表2可以看出,只有引力辐射阻尼对轨道半径产生的长期效应同引力常数变化产生的长期效应相一致。而对轨道偏心率除前者有混合长期项外两者皆有周期项。两者在长期效应可在量级上比较。

[1] Dirac P A M.The cosmological constant[J].Nature,1937,139:323.
[2] Dirac P A M.A New basis for cosmology[J].Proc R Soc London A,1938,A165:199-208.
[3] Kholchevnikov C,Fracassins M.La Probleme dex edeux corps avec G variable selon l’hypothese de Dirac[J].Conferenze Dell’Osservatorio Astronomico di Milano Serie 1,1968, 9:1-50.
[4] Hut P,Verhulst F.The two-body problem with a decreasing gravitational constant[J]. M N R A S,1976,177:545-549.
[5] Bishop N T,Landsberg P T.Time-Varing Newtonian gravity and universal motion[J]. Nature,1976,264(25):346-347.
[6] Maiti S R.Time-varying gravitation in Newtonian theory[J].MNRAS,1978,185:293-295.
[7] Brouwer D,Clemence C M.Method of Celestial Mechanics[M].Academic press,New York and London,1961.
[8] http://binaries.boulder.swri.edu/atlas/.
[9] AI-Rawaf A S.Limits on the changes in the gravitational constant from nucleosynthesis [J].Astrophys &Space Sci,2007,310(1-2):173-175.
[10] 李林森.双星多方模型的形状及其对同步子星轨道要素的摄动影响[J].云南天文台刊,1997,(4):9-167.
Li Linsen.Configuration of the Polytropic Model of Binary Star and Its Perturbation Influence on the Orbital Elements of the Synchronous Components in Close Binary Sysetm[J].Publications of The Yunnan Observatory,1997,(4):9-17.
[11] 李林森.天体轨道要素变化的后牛顿效应[J].中国科学,A辑(数学物理学天文学技术科学)1988,31(5):523-529.
[12] 李林森.双星系中两子星的自转对双星轨道变化的后牛顿效应[J].天文学报,2001,42(4):428-435.
Li Linsen.The Post-newtonian Effects Due to Rotation of Stars on the Variation of the Orbital Elements of the Component in Binary System[J].Acta Astronomica Sinica,2001,42(4):428-435.
[13] 李林森.引力辐射阻尼对双星轨道要素变化的影响[J].物理学报,1989,38(11):1877-1881.
Li Linsen.The effect of gravitational radiation damping on the Variation of the orbital elements of binary systems[J].Acta Phrysica Sinica,1989,38(11):1877-1881.
[14] Khajavi M,Edalate M T,Jassur D M Z.BVRI photometry and light curve analysis of V W Cep[J].Astrophys & Space Sci,2002,282(4):645-653.
