基于动力测试的高速铁路大跨连续梁桥混凝土弹性模量识别研究

赵永军

(中铁十六局集团第五工程有限公司,河北唐山 063030)

1 概述

弹性模量是混凝土力学性能指标中一个重要物理参数,是结构质量评价中一个重要的参考指标,而影响混凝土弹性模量的因素有很多,如密实度,湿度,温度,骨料等,因此,实际结构的弹性模量与标准试件弹性模量存在较大的差别。对于采用悬臂施工的高速铁路大跨连续梁桥,纵向划分节段较多使各节段混凝土由于实际施工条件的不同有所差异,施工周期长更使结构的施工条件发生较大的变化。综合以上各种影响因素,如果采用试件弹性模量评价实际结构将存在较大偏差。一般情况下,基于结构实际变形观测代入结构力学平衡方程也可得到反映整体结构的弹性模量,然而对于大跨度悬臂施工连续梁桥而言,结构由于受风、施工等影响,结构变形观测值容易偏离实际情况,存在一定误差。结构动力特性测试,特别是基于环境激励作用进行结构动力测试时,这些因素甚至可以成为有利因素,因此,本文基于桥梁在悬臂施工状态下的动力特征值推导计算得出结构的弹性模量,并与试件弹性模量进行对比分析,引入一种更为准确的弹性模量识别方法,从而为评价结构施工质量提供更为可靠的参考指标,并可以为工程师、科研工作者建立更为准确的结构计算模型提供更为符合实际的结构基本参数。

2 工程背景

武广铁路客运专线王灌冲大桥位于湖南省株洲市,横跨京珠高速公路,主跨采用(70+125+70)m双线预应力混凝土连续梁。主梁采用箱梁结构,主梁根部梁高920 cm,跨中梁高520.1 cm。混凝土强度等级为C55,采用挂篮悬臂施工；两边跨现浇段均采用满堂支架施工。设计荷载为ZK活载,见图1、图2。

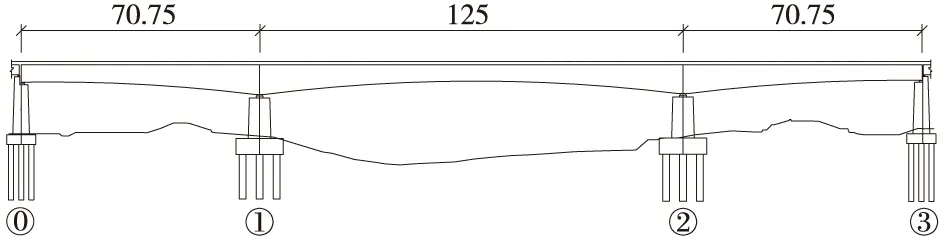
图1 王灌冲大桥主桥布置(单位：m)

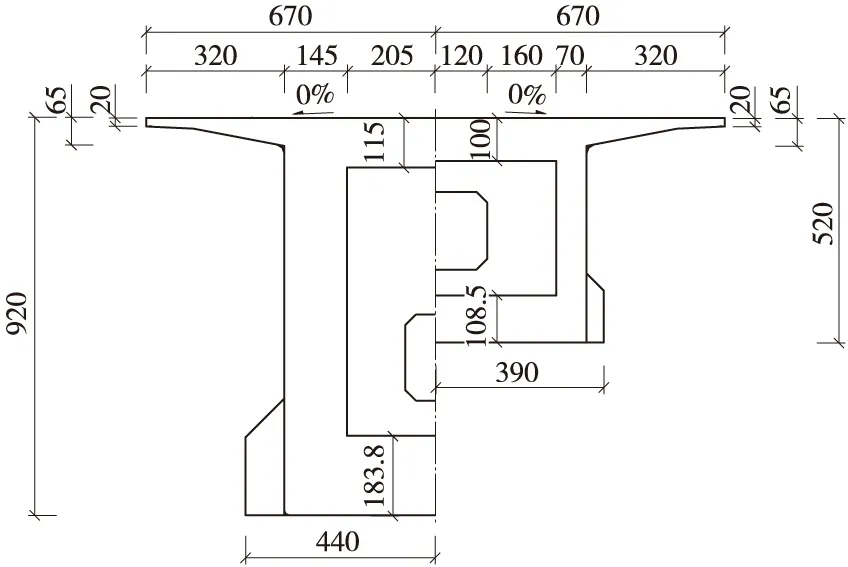
图2 0(16)号段截面(单位：cm)

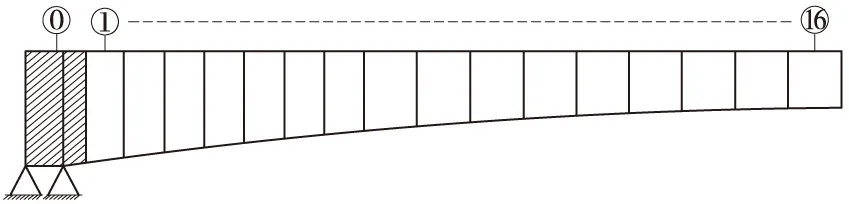
图3 半立面(0—16号段)

3 试验分析

3.1 试验概况

本桥采用悬臂对称施工,桥梁施工节段划分为4.5 m+7×3 m+9×4 m=61.5 m(图3),本文取桥梁最大悬臂状态即图3中第16号节段施工阶段进行动力测试。

试验仪器：德国HBM动力测试仪器一套,采用环境激励采集数据,采样频率50 Hz,结构为对称结构取一半结构布置测点,测点布置于桥梁箱梁顶面对应于腹板位置处,见图4。

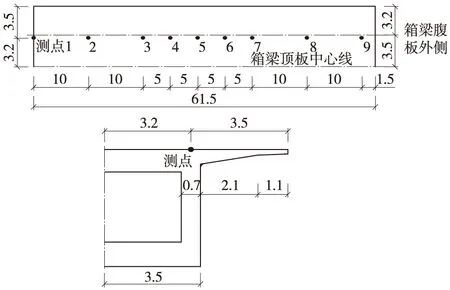
图4 测点布置(单位：m)

3.2 试验结果

将采集数据进行分析处理得到结构动力特性,结果见图5、图6。

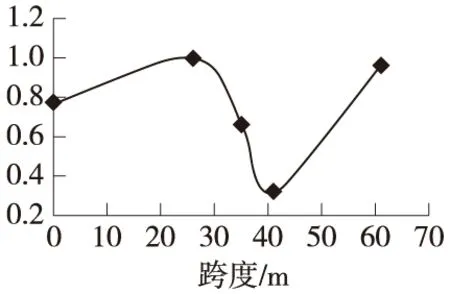
图5 1号墩16号段第六阶振型

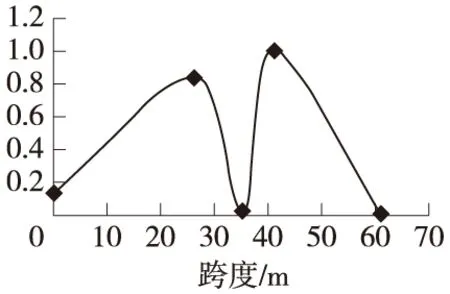
图6 1号墩16号段第九阶振型

4 弹性模量识别

4.1 建立动力特性方程

首先建立结构动力特性方程,本文连续梁桥梁截面形式为变截面箱形梁,梁高、腹板、顶板、底板沿纵向均有变化,建立结构动力方程后,应用解析方法计算困难,通常利用数值解法进行计算,综合比较文献[1～2]所用方法,本文引入文献[2]所述方法,以便于得到精度较高的单元划分,并便于计算程序编制。

设梁体单位梁长质量为m(x),惯性矩为I(x),梁体自由振动微分方程可表示为

将梁用等步长h=0.1 m划分为615个单元,在每一分段线上设置一个节点,有

其中

a1i=ki[(cosαi+sinαithαi)tanαi+

(shαi+chαitanαi)thαi]

a2i=ki[(shαi-cosαi)+(chαitanαi-

sinαithαi)

a3i=-2ki[(shαi+chαitanαi)(cosαi-

sinαithαi)

a4i=a1ia5i=-a3i

b1i=ki[(cosαi-sinαicthαi)cotαi+

(chαi-shαicotαi)cthαi]

b2i=ki[(chαi+cosαi)-(shαicotαi+

sinαicthαi)

b3i=-2[(chαi+shαicotαi)(cosαi-

sinαitanαi)

b4i=-b1ib5i=b2i

αi=kih

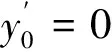
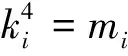
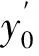
由此可知式(4)中,其他参数均是作为已知量,仅频率ω为未知量,且[Y]振动时不恒为零,则下式即为结构频率方程

|[L]|=0 (5)

4.2 求解弹性模量方程的建立

将实测结构频率作为已知量代入式(5)中的频率ω,这样频率方程中仅余弹性模量作为未知量,由此频率方程也转变为求解弹性模量方程,即

4.3 计算结果对比分析

将试验采集数据识别得到的桥梁自振频率代入式(6),编制相应计算程序,即可解出相应频率下的桥梁结构弹性模量值(表1)，与试件弹性模量进行对比。为便于两者比较,本文定义“综合弹性模量值”,即：将试件弹性模量按结构节段质量进行加权平均而得到的弹性模量。

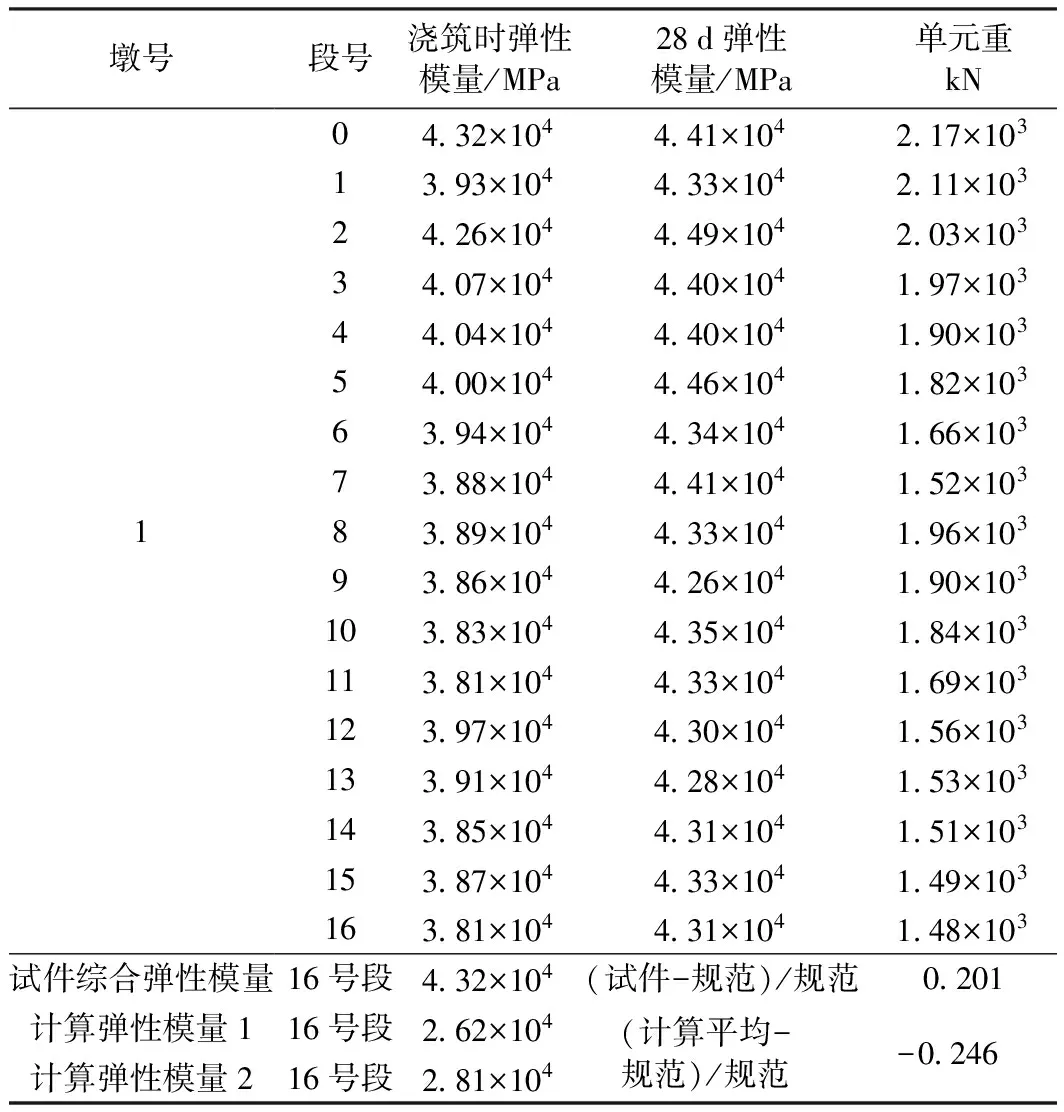
表1 计算弹性模量与试件弹性模量

注：表中试件综合弹性模量由各施工节段占全桥比重以试件弹性模量计算而得,其中养护期满28 d的节段弹性模量按28 d弹性模量计算,不足28 d的按养护天数与初始值和28 d弹性模量插值计算得到,计算弹性模量1表示由第6阶频率计算得到的弹性模量,计算弹性模量2表示由第9阶频率计算得到的弹性模量。

由表1可见：由结构动力特性值计算推得的弹性模量小于由试件弹性模量所表征的综合弹性模量,由文献[3]知,轴向力引起刚度折减,结构预应力含轴向力分量,根据结构刚度与弹性模量的关系可知,由动力特性反推计算得到的弹性模量已包含轴向力引起的刚度折减效应,应略低于实际结构弹性模量。文中的结果基本符合上述规律,而根据试件弹性模量表征的综合弹性模量超出计算所得弹性模量较多,与实际结构弹性模量偏差相应更大,而由此判断结构实际施工质量,必然存在较大偏差,为今后的结构安全也埋下了隐患,因此,本文所提出的利用实测得到的结构动力特性反推计算结构弹性量,对结构质量评断更有可靠的参考意义,同时由此获得的较为符合结构实际的弹性模量指标也可用于结构后期的理论计算中,从而得到更为符合实际的理论计算结果。

5 结语

本文通过采用动力测试仪器采集识别频率并由此计算其结构整体弹性模量,并与由试件弹性模量评价对比,得到较为真实的桥梁结构力学特性,为桥梁施工质量评价提供参考,具有较大的现实意义。

(1)由于桥梁结构属于多自由度体系,必然存在多阶振动模态,利用实测得到的结构多阶模态作为已知量,代入频率方程求解结构弹性模量,可以得到多个弹性模量值,结构弹性模量在结构正常状态下是稳定的,因此利用概率统计可以计算得到一个近似的真值,由此真值作为评价指标更准确更可靠,这对准确评价桥梁结构的施工质量是很有意义的。

(2)本文取大跨度桥梁最大悬臂状态进行动力测试的研究意义在于：结构最大悬臂状态时结构已接近成桥状态,由此得到的还可与成桥阶段以此法计算推得的弹性模量对比分析，提高弹性模量识别的准确度。

(3)本文的研究意义还在于：准确识别结构物理特性参数,由此,工程工作人员以及科研人员可以建立更为准确的计算模型,以便用于对结构运营期真实状态的预测,及早发现问题解决问题；

(4)本文限于试验条件较差,高速铁路大跨度连续梁桥结构刚度很大,通常的环境激励(风,交通等)无法引起结构的自由振动,振动信号微弱,环境噪声以及仪器自身的误差将大部分结构振动信号淹没掉,因此试验采集得到的数据识别效果不佳,这也与笔者起初的设想有较大的出入。因此,应根据实际结构的结构特点选取合适的测试方法,如锤击法等。

(5)本文试验时桥梁处于施工阶段,在某些情况下：挂篮移动过程中,混凝土浇筑后挂篮锚固未松等的力学模型不明确,而又无法干预施工进程,这也就使得本文计算结果的准确度有所折扣,因此为保证准确度以后可以先考虑试验室试验。

(6)本文暂未考虑预应力对结构刚度折减效应的影响,而要更加准确的评价结构弹性模量时,必须准确得到结构预应力效应,并得到相应准确的结构刚度折减效应,这些都值得再做研究。

[1] 朱勇涛,易传云.变截面梁弯剪振动的传递矩阵法求解[J].机械传动,2002(2)．

[2] 刘礼华,周剑波,雷仲庄.变截面梁振动问题的一种数值计算方法[J].武汉水利电力大学学报，1996(5)．

[3] 刘晶波,杜修力.结构动力学[M].北京：机械工业出版社，2005．