基于灰色GM(1,1)和灰色-马尔可夫模型的轨道几何不平顺预测及应用研究
2010-01-22潘海泽黄远春刘仍奎胥耀方
潘海泽,黄远春,,汪 磊,刘仍奎,胥耀方
(1.上海工程技术大学城市轨道交通学院,上海 201620; 2.北京交通大学轨道交通安全与控制国家重点实验室,北京 100044;3.北京交通大学交通长江学者研究中心,北京 100044)
我国新建200 km/h的客货共线铁路,既有线也提速到200 km/h。速度高、轴重大、运行条件复杂,对线路的整体平顺性提出了更严格的要求[1~3]。轨道质量状态的评价主要依靠轨检车的检测数据,其方法有2种:一种是通过峰值管理来评价线路的状态;另一种是均值管理,用轨道不平顺统计特征值,即轨道质量指数(TQI)来评价轨道状态[4~6]。欧美及日本等许多国家的铁路也都用轨道谱诊断和综合评判铁路轨道的平顺性。欧洲高速铁路采用轨道谱反演曲线的上、下限界谱,对轨道的平顺性进行评判[7~11]。
轨道不平顺的评价指标一般有峰值和区段内的标准差两种[12~13],但鉴于这2种指标无法反映不平顺波长的影响,因此有学者又增加了利用功率谱指标来评价轨道不平顺的方法,故描述轨道不平顺状态一般有3个指标:不平顺的最大值、不平顺的区段标准差、不平顺的功率谱[14~16]。本文主要研究几何形位不平顺的状态影响。在分析国外轨道几何不平顺预测模型的基础上,结合国内的实际情况,对轨道不平顺的区段标准差提出不同方法建立预测模型,并对预测结果进行分析比选。
1 灰色预测模型的建立及应用研究
1.1 灰色预测模型GM(1,1)的基本原理
GM(1,1)反映了一个变量对时间的一阶微分函数,其相应的微分方程为
式中,x(1)为经过一次累加生成的数列;t为时间;a,u为待估参数,分别称为发展灰数和内生控制灰数[6]。建立一次累加生成数列。设原始数列为
x(0)={x(0)(1),x(0)(2),x(0)(3),…,x(0)(n)},
i=1,2,…,n
按下述方法做一次累加,得到生成数列(n为样本空间)
(1)利用最小二乘法求参数a、u。设
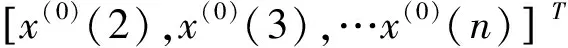
参数辨识a、u
(2)求出GM(1,1)的模型
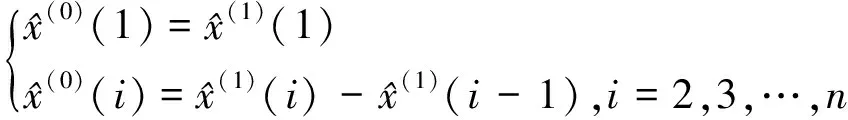
(3)对模型精度的检验。检验的方法有相对误差检验、残差检验、关联度检验和后验差检验。
首先计算原始数列x(0)(i)的均方差S0。其定义为
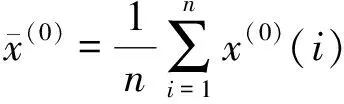
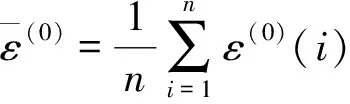
最后根据预测精度等级划分表(表1),检验得出模型的预测精度。
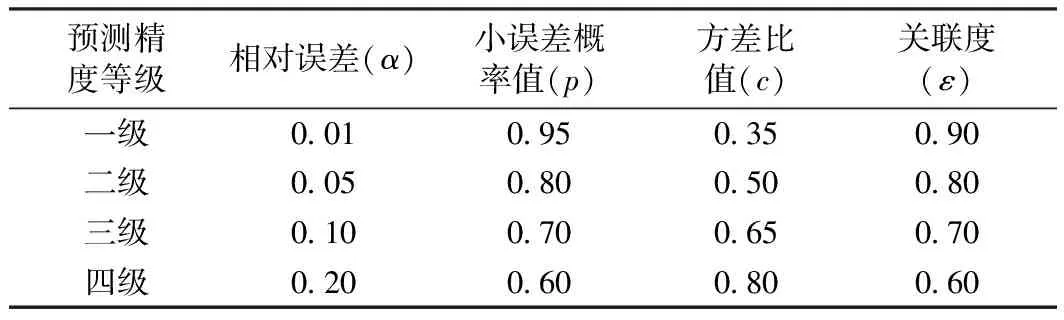
表1 预测精度等级划分
(4)如果检验合格,则可以用模型进行预测。即用
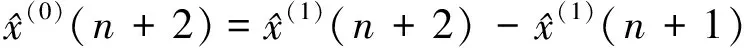
作为x(0)(n+1),x(0)(n+2),……的预测值。
1.2 基于GM(1,1)模型的TQI预测
数据选取轨检车检测数据库中沪昆线上行的数据,检测时间分别为2008年4月第1遍、2008年4月第2遍、2008年5月第1遍、2008年5月第2遍、2008年6月第1遍、2008年6月第2遍,预测的时间为2008年7月第1遍,间隔时间为90 d。长度上分别选取工务段、车间、工区管辖范围内的线路长度的平均TQI以及1 km和200 m的TQI数据,作者利用灰色预测原理设计并开发了相应软件以便计算。以下为此软件的计算预测结果。
(1)曲靖工务段(K2 471~K2 532)的TQI预测。通过软件进行预测,预测结果如图1所示。
平均相对误差为0.004 038,小于0.01,Δ6=0.004 36<0.01,所以预测精度为一级。
预测的结果为11.636 0,实际检测值为12.13。

图1 曲靖工务段(K2 471~K2 532)的TQI预测
(2)K2 500 TQI预测。

图2 K2 500 TQI预测
(3)多里程点(K2 500~K2 520)TQI预测,单元区段为200 m。预测结果及预测的绝对误差见图3、图4。
图3 多里程点(K2 500~K2 520)TQI预测
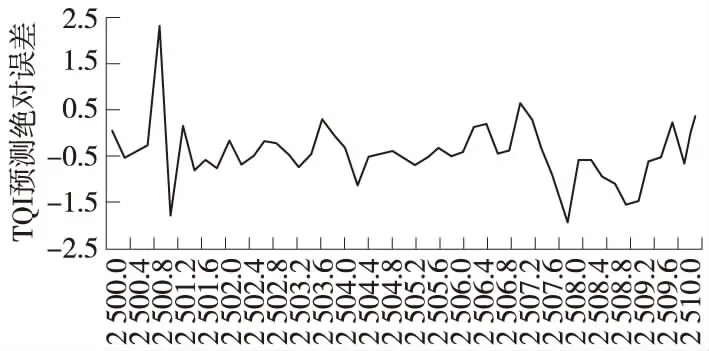
图4 多里程点(K2 500~K2 520)TQI预测绝对误差
1.3 灰色预测模型预测结果分析
将以上分析的一元线性回归的预测结果和灰色预测模型的结果归纳如表2所示。
由表2的统计结果可以发现,灰色预测模型预测结果比一元线性回归分析模型的精确度有所提高。其主要原因是,灰色预测的累积运算有效减少的数据随机波动性的影响。与一元线性回归相比,灰色预测能在各种里程范围内都取得较好的预测结果。但是不论是一元线性回归还是灰色预测,对短区段的TQI预测偏差较大。
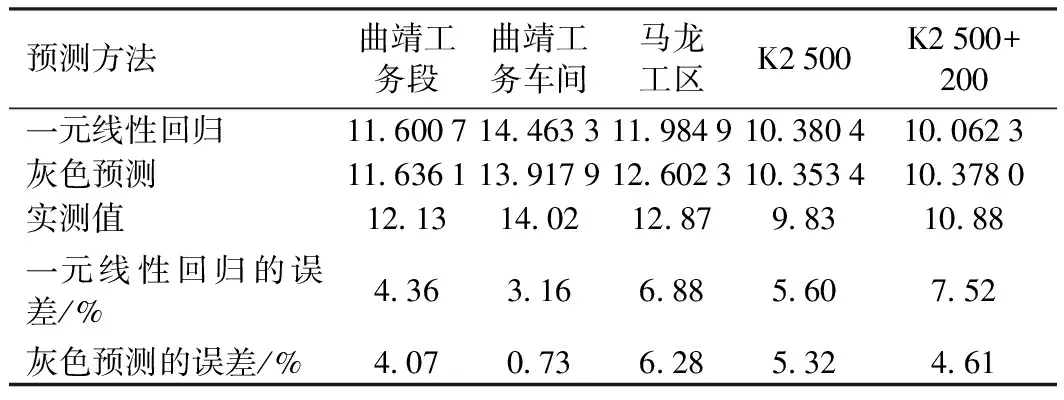
表2 TQI预测结果汇总
2 灰色-马尔可夫预测模型
灰色预测的优势在于短期预测,缺点在于对长期预测和波动较大数据序列的拟合较差。而马尔可夫预测的对象是一个随机变化的动态系统,对于长期预测和随机波动较大的数据序列的预测效果较好,但是,马尔可夫预测对象要求具有平移过程。将灰色预测与马尔可夫预测两者结合起来,形成灰色-马尔可夫预测模型,不仅能揭示数据序列的发展变化总趋势,又能预测状态规律。用马尔可夫预测方法对于解决无后效性的预测有独到之处,两者结合不仅避免考虑其他多种影响因素,还可使预测具有较强的科学性和实用性。
2.1 灰色-马尔可夫预测模型原理
应用灰色-马尔可夫预测模型进行预测的基本思路是[17]:
(2)状态划分:以γ′(k)曲线为基准,划分成与γ′(k)曲线平行的若干条形区域,每个条形区域构成一个状态,任意状态区间Qi表示为Qi=[Q1i,Q2i],(i=0,1,2,…,T)。式中:Q1i=γ′(k)+Ai,Q2i=γ′(k)+Bi,Ai,Bi可根据具体情况自行确定,显然状态Qi具有时态性。
(3)计算转移概率矩阵:公式为
Pij(m)=Mij(m)/mi(i,j=1,2,3…,T)(6)
式中,Pij(m)为由状态Qi经过m步转移到Qj的概率;T为划分状态数组;Mi为原始数据按一定概率落入状态Qi的样本数;Mij(m)为由状态Qi经m步转移到Qj的原始数据样本数。
当状态划分不太合适,以至于某一状态中无原始数据落入时,则可令Pij(m)=Pji(m)=0。由此,可求出状态转移概率矩阵p(m)来预测未来状态转向
(7)
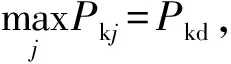
(4)确定预测值:当Qd确定后,也就确定了预测值的变动区间[Q1d,Q2d],则有
(8)
(5)模型精度检验:检验公式为
ε(k)=q(0)(k)/x(0)(k)
式中,q(0)(k)为残差;ε(k)为相对误差。
2.2 模型计算及分析
如上文所述灰色-马尔可夫适用于长期预测和随机性较大的预测,所以本节将此灰色-马尔可夫预测模型分别应用于较小区间范围(1 km,随机性较大),较短时间(15 d)和较长时间范围(45 d)的TQI预测。
(1)较短时间范围的TQI预测
如上文所述灰色-马尔可夫适用于长期预测和随机性较大的预测,所以本论文将此模型应用于小区间的预测(1 km和200 m的单元区段,随机性较大)。下面以1 km区段为例来描述模型的应用。
步骤 1:建立灰色 GM(1,1)模型。
由本文2.1节直接获得灰色GM(1,1)预测公式
(9)
式中a=-0.001 791 78,u/a=10.233 632 17
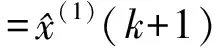
γ′=(10.16,10.261 026,10.279 428,10.277 863,10.316 331,10.334 833,10.353 367)。预测结果如图5所示。

图5 K2 500 TQI预测
步骤 2:状态划分。
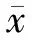
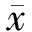
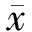
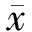
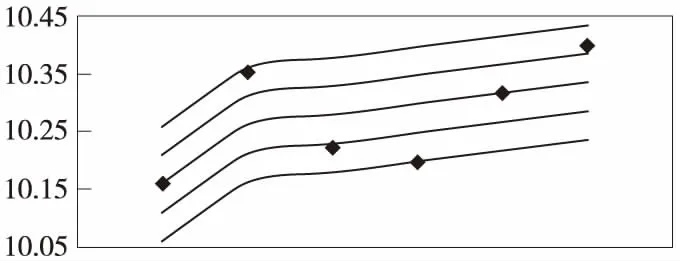
图6 状态划分
步骤3:计算状态转移概率矩阵。
在状态划分图中,横坐标表示时间,纵坐标为TQI值;实线为趋势曲线,相邻两实线之间为一状态,点为原始数据。根据状态划分图,容易计算出一步转移概率矩阵为

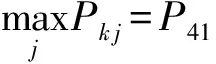
则可认为2007年6月第2遍检测TQI值处于状态⊗1,所以2007年7月第1遍检测TQI预测值为
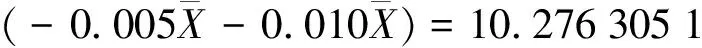
2007年7月下半月TQI预测值与实际值比较见表3。

表3 TQI对照(短时间)
(2)较长时间范围的TQI预测
数据的选取和预测的步骤都同上,将灰色-马尔可夫模型与一元线性回归分析模型与灰色预测模型的预测结果对照见表4。

表4 TQI对照
(3)结果分析
由以上预测分析可见,当原始数据存在随机波动性时(如本研究实例),应用灰色-马尔可夫组合预测方法进行预测,比直接应用灰色GM(1,1)模型预测更能反映TQI值的变化,短期预测精确度达到95.46%,提高了0.78%。长期预测达到了95.93%,比灰色预测提高了2.49%。因此,利用灰色-马尔可夫组合预测方法,分析和预测时间序列数据信息,不仅可以避免自然环境、人的主观因素等影响,还可以提高预测精确度,具有较强的科学性和实用性。
3 结 论
轨道结构的变形是无法避免的,其影响因素很多,目前,国内尚缺乏一个能全面反映轨道不平顺发展的预测公式。本文基于昆明铁路局的实际数据,提出了灰色预测模型和灰色-马尔可夫预测模型。通过将两种模型预测结果与一元线形回归的预测结果对比分析,得出下列结论。
(1)TQI的灰色预测模型,不仅适用于较长区段的TQI预测,对于更长区段的TQI预测也有比较好的效果,所以适用范围更为广泛,但是模型的计算过程相对复杂。
(2)灰色-马尔可夫预测模型在灰色模型的基础上,利用状态转移矩阵进一步降低由不平顺变化的随机性带来的影响,不仅能够预测随机性较强的TQI数据,也能应用于较长时间范围内的预测。但由于要建立复杂的状态转移矩阵和需要大量的检测数据来建立状态转移矩阵,所以需要进一步的收集历史检测数据才能更好的进行轨道不平顺的预测。
[1] 许玉德,周 宇.既有线轨道质量指数的分布与不平顺权重系数统计分析[J].中国铁道科学,2006,27(4):71-73.
[2] 陈宪麦,王 澜,陶夏新等. 我国干线铁路轨道平顺性评判方法的研究[J].中国铁道科学,2008,29(4):21-22.
[3] 张格明.160 km/h线路轨道不平顺管理标准的研究[J].中国铁道科学,1995,16(4):31-41.
[4] 陈宪麦,王 澜,陶夏新,等.我国干线铁路通用轨道谱的研究[J].中国铁道科学,2008,29(3):73-77.
[5] 周 正,赵国堂.轨道质量指数计算问题的探讨[J].中国铁道科学,2003,24(3):64-68.
[6] 周 宇,练松良.基于遗传算法的轨道综合养护决策系统的研究[J].中国铁道科学,2008,29(6):132-134.
[7] Coudert F, Sunaga Y, Takegami K. Use of Axle Box Acceleration to Detect Track and Rail Irregularities[C]. WCRR, 1999.
[8] Bocciolone M, Coprioli A, Cigada A. A measurement system for quick rail inspection and effective track maintenance stragety[J]. Mechanical systems and signal processing, 2007,21(3):1242-1254.
[9] Caprioli A, Cigada A, Raveglia D. A benchmark between the wavelet approach and the more conventional Fourier analysis[J]. Mechanical systems and signal processing, 2007,21(2):631-652.
[10] Fausto Pedro García Mrquez,Diego Jose Pedregal Tercero.Unobserved Component models applied to the assessment of wear in railway points: A case study[J]. European Journal of Operational Research, 2007,176(3):1703-1712.
[11] Iwnicke S.D, Grassie S, Kik W. “Track Settlement Prediction using Computer Simulation Tools”[R/OL]. The Rail Technology Unit, 2004.
[12] 王建西,李海锋,许玉德.基于概率分布推移变化的铁路轨道几何状态评价与预测方法[J].中国铁道科学,2008,29(5):31-34.
[13] 练松良,陆惠明.轨道不平顺分析程序[J].中国铁道科学,2006,27(1):68-71.
[14] 张曙光,康熊,刘秀波.京津城际铁路轨道不平顺谱特征分析[J].中国铁道科学,2008,29(5):25-30.
[15] 罗林,张格明,吴旺青,等. 轮轨系统轨道平顺状态的控制[M].北京:中国铁道出版社,2006.
[16] 陈宪麦,王 澜,杨凤春,等. 用于铁路轨道不平顺预测的综合因子法[J].中国铁道科学,2006,27(6):27-31.
[17] 石 扬.基于灰色马尔可夫模型的能耗预测[J].山东轻工业学院学报,2009,23(2):63-64.
