基于WLs的二维地球化学景观多重分形建模

高 歆

(中国地质大学(北京)地球科学与资源学院， 北京 100083)

利用多重分形理论建模构成了过去数十年来客观自然现象比较流行的一种尺度分析手段，广泛的被应用在包括地学、湍流和因特网等自然科学领域中。为了有效的指导地球化学勘探和矿产资源评价，Mandelbrot和Cheng[1-2]提出了多种多重分形模型来描述地球化学数据的空间尺度结构，这些新的模型不仅考虑地壳中矿石元素的分布几何形状，而且将传统的地质统计学纳入到了计算分维谱的框架之下，其中尤其是数据域的奇异性分析，即计算空间中每点的奇异值，一种高通滤波方式，可以有效的从由各种地质过程生成的混合模式和特征中分解背景值和异常值。

对多重分形谱的估计是多重分形分析的重要任务。针对多重分形谱建模，有两种最常用的建模方法，其中一种是基于分维谱f(α)，另外一种是基于余维数c(γ)。两种模型之间的内在联系现已得到证明[3]。多重分形理论已广泛用于各种学科领域，并因此产生了各种各样的计算多重分形谱函数的方法，如矩方法[4]、直方图法、小波方法[5],以及二次维矩法[6]等，其中应用最广泛的是将空间分成许多格子的矩统计方法。另外，多重分形模型将服从正态或者对数正态分布的微量元素的背景值与服从分形分布(幂律分布)的高低异常值统一到多重分形谱中，多重分形分析体现了统计手段上的进步,目前地学数据处理中，最常用到的是基于盒子的多重分析方法。Cheng等[7]通过频率-浓度、数量-浓度、浓度-浓度、浓度-周长、S-A等分形模型及矩分析等多重分形方法，将地球化学异常从背景中分离出来；郭科等[8]运用多重分形模型，通过研究Pb、Zn、Sb、Ag、Cu共五种元素的广义分形维数Dq，认为这些元素在空间上的分布服从多重分形分布特征，同时指出多重分形方法相比于传统的化探方法来说在判断元素的共生组合方面具有一定的优越性。Zheng等[9]运用周长-面积等分形学研究方法研究了中国3个金矿床中黄铁矿、雄黄等矿物表面As、S、Fe、Si等元素在成矿过程中的迁移和转换规律。

自从Parish和Frisch[10]提出用湍流域中的速度增量来刻画尺度函数：Sp(l)=<(δfl)p>～lξp，δfl(x)=f(x+l)-f(x)是尺度域中的增量。不幸的是，Muzy[11]发现了该种方法只能刻画信号中比较强的奇异性，对于一些弱的奇异性和谱值左半部分显得无能为力。Mallat[12]提出了利用小波极大模值捕捉信号的奇异性以来，Arneodo等人提出了WTMM代替直接的速度增量来计算尺度函数，从而避免了上述缺点。然而，WTMM需要连续小波变换，以及利用不同的半径在不同的尺度上进行搜索邻域中的模极大值，复杂的计算过程，高昂的计算量都使的这种方法变的不很实用。为了避免上述所述WTMM涉及到的繁琐的工作量，法国数据学Jaffard[13]等人提出了WLs的计算方法，不仅能够描述谱值的整个区域，还避免了连续小波变换以及寻值等繁琐步骤。多次研究证明，计算分形谱的方法严重依赖方法和数据本身，WLs的引入为这种情况提供了一种补充。Dojnow[14]通过基于小波系数的多重分形模型，考察了含有噪声信号的多条脑电图曲线，指出分析信号的相位携带了最多的尺度不变性信息；Khalil等[15]利用基于WTMM的多重分形模型考察了间歇染色体结构，将染色体版图从背景中分离出来，提出了一种新的边界分割方法，阐述了染色体结构、位置和不稳定性之间的潜在关系。

1 基于盒子的多重分形分析

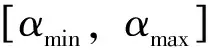
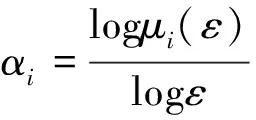
(1)

这里的非整数αi称为coarse holder指数[16]。把在分形上具有相同α值的小盒子数目记为Nα(ε)，它与ε的大小有关，并且可以写成：

(2)

将上式与N(ε)～ε-D的简单分形公式对比，可见f(α)的物理意义是表示具有相同α值的子集的分形维数，或者说它描述了ε→0+直方图N(ε)的变化，f(α)定义为具有相同α值的子集的Hausdorff维数，称为多重分形谱或奇异性谱。在多重分形谱的众多计算方法当中，矩方法是最常用的方法之一。为了解f(α)的分布特性，定义分割函数：

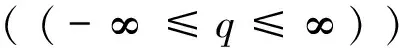
(3)

可以获得质量指数函数τ(q)，τ(q)是关于q的凸函数。当q=1时达到最大曲率，该点的曲率可以用于判断是否具有多重分形性。通过勒让德变换，可以得到α(q)和f(α)如下的两个函数：

(4)

三个函数τ(q)、α(q)和f(α)是相互关联的。

2 基于WLs的多重分形分析

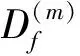
(5)

继续设H0(k)和G0(k)为两个具有有限冲击响应的滤波器，引入二进区间以及并集：

λj,k1,k2={[k12j,(k1+1)2j],[k22j,

(6)

(7)

理论上的WLs定义为(图1)

(8)

图1 WL的定义示意图

WLs正是通过其局部奇异性刻画能力构成了了尺度分析模型，如果X(t)在t0点存在奇异性指数α(t0)≥0，消失矩Nψ≥α(t0)，WLs与尺度之间的幂律关系为：

(9)

通过计算位于尺度2j上的WLs的q阶矩的平均值，可以得到结构函数和质量指数函数。

(10)

(11)

通过勒让德变换，奇异值函数和分维谱函数定义为：

(12)

同样，这三个函数τL(q)、αL(q)和fL(α)是相互联系的。

3 方法验证

3.1 De Wijs模拟数据

为了对比这两种方法的分析效果，本文采用De Wijs模拟数据[18]验证包括N=64和N=1028两种不同尺度数据，生成算子为1.96、0.84、0.84、0.36。图2是尺度指数和多重分形谱的估计值，对于两种不同数据盒子估计法均获得了比较的拟合，但是在谱值的首末端有点偏差，主要是由于边缘效应造成的。结果表明，对于小尺度的模拟数据，图2A中与理论曲线相比，质量指数曲线在左边和右边分别出现了上移和下移的情况，相应的谱值左边和右边偏离标准的谱域，因为基于WLs的计算中对原小波系数进行挑选导致的发散，而基于盒子法的估计比较接近理论值，也显示了盒子法对于小尺度的测度数据的稳定性和准确性。同样，值得注意的是，对于n=1的消失矩WLs估计，原理上等同于盒子法(盒子法：测度上的求和或者积分，一阶消失矩：加权求和或者积分)，谱值的左边现实了良好的逼近，即模拟数据中的小值模拟准确，而对于大值出现了偏差。对于大尺度多重分形分析，盒子估计法和WLs的基本都和理论曲线实现了基本重叠，表明对于大尺度数据，WLs和盒子估计都可以用来多重分形分析。总之，对于小尺度的逼近，由于分辨率有限，边缘效应，以及高阶消失矩的过分平滑都会导致估计发散，而对于大尺度的数据，两者都可以作为分析手段，对于消失矩，可以去2、3、4阶的均值来近似估计。

3.2 地球化学数据验证

本文地球化学数据验证来自云南个旧锡矿水系沉积物元素Sn、Cu和Pb(图3)，研究区域为29400 km2，，采样间隔为2km，分辨率为2km×2km，N=76×50，分析小波为Daubechies，消失矩为Nψ=1,2,3,4。如图4所示，对于Sn元素谱值估计，基于WLs不同的消失矩的计算，差别明显，显示了WLs估计得不稳定性，而Cu和Pb的估计，在左边还表示了部分的重叠，正则性方面强于Sn元素。另外，利用经典级联过程验证多重分形数据的正则性，也可获得同样的结果，本文限于篇幅，另文阐述。通过地球化学元素数据的验证，盒子估计法展现出来了优良的稳定性和准确性，对于小尺度数据WLs估计需慎重。从另外的角度来说，利用基于函数奇异性的这套框架某种程度上不符合以测度刻画的地学数据，或许WLs优势在于震荡的一维信号。

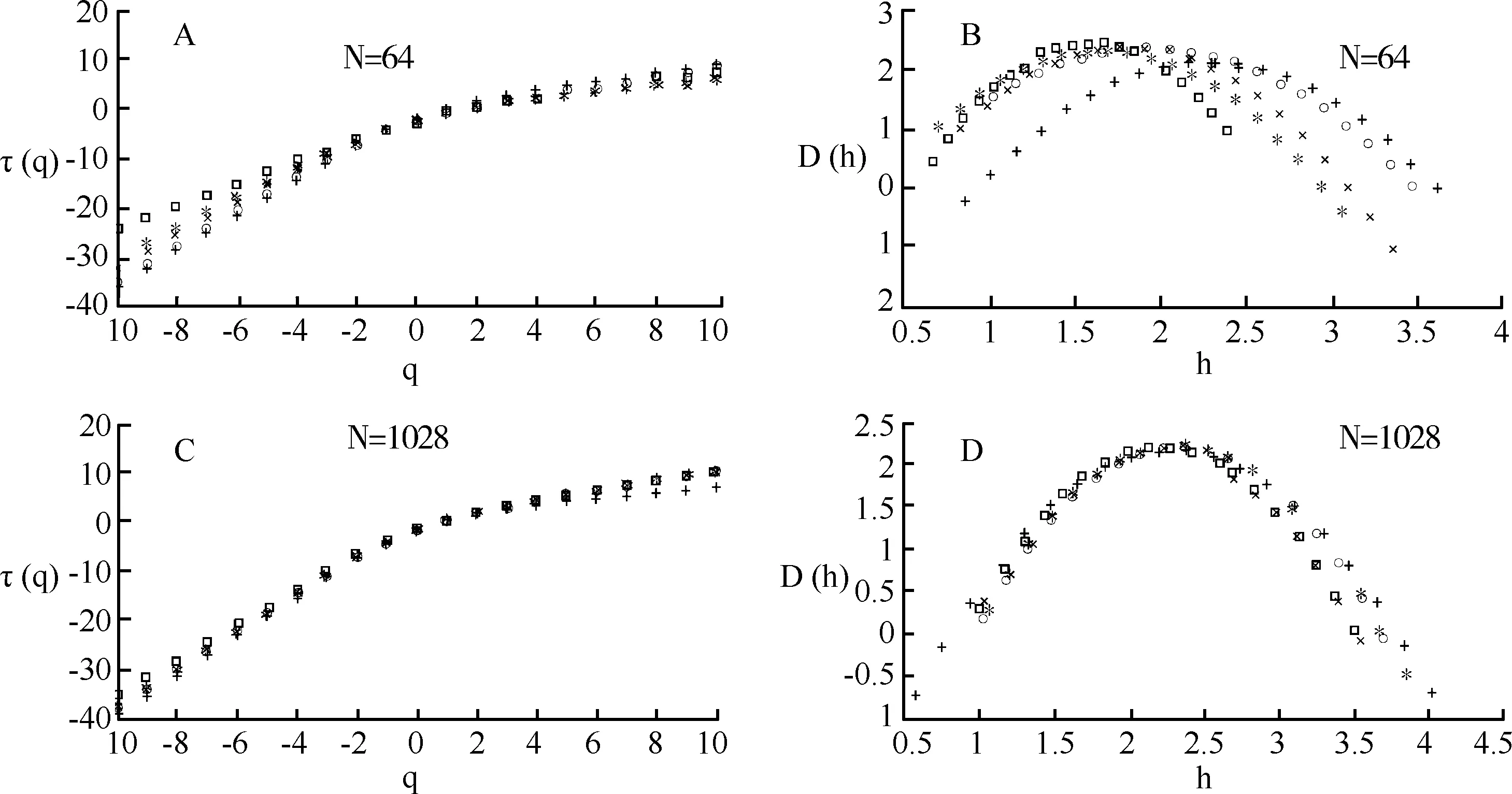
图2 De Wijs模拟数据的质量指数和分形谱(盒子法: “+”；WL:消失矩N=1,2,3,4，符号：“o”;“×”; “*”; “矩形”)

图3 云南个旧水系沉积物Sn、Cu和Pb元素IDW插值图(A-C: 分别为Sn、Cu和Pb元素浓度值)

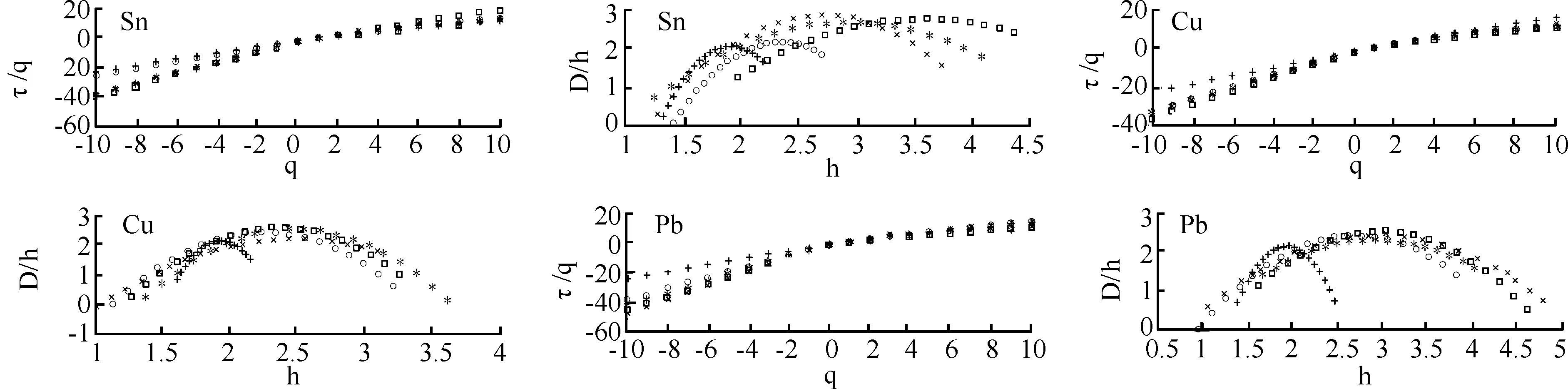
图4 地球化学元素数据的质量指数和分形谱(盒子法: “+”；WL:消失矩N=1,2,3,4，符号：“o”; “×”; “*”; “矩形”)

4 结论

对于分辨率有限、大小且不规则的现实地学数据，基于WLs的尺度分析，在准确性和稳定性方面都弱于盒子法，但是有时候尺度分析并不涉及到其多重分形谱的计算，仅仅利用系数与尺度之间的幂律关系，需要找到一个拐点，因此，小波系数不失为找不同尺度阈值一个好方法。对于小波消失矩的选择，消失矩过小，捕捉奇异性的强度不够，过大会导致分析的数据滤波过于平滑，从而导致谱值的两端发散，因此，一般取消失矩的比较大的加权平均较合适。另外，基于WLs的估计涉及到小波变换的多分辨率分析，在图像分割过程中，利用小波刻画的奇异性进行分割有着内在的优越性，延伸继续刻画多重分形谱，正如前文引用，是一个有效的方法。

这篇文章主要讨论了以积分为主的测度和以累积量为主的尺度分析，以经典矿物分割模型de Wijs模型模拟数据为例，结果表明，对于盒子法的尺度分析，不管是小尺度还是大尺度，都表现出了更优的结果，基于WLs的尺度分析对于大尺度的数据也表现出了良好的结果。此外，基于小波系数的WLs不仅可以为分析数据提供多分辨率分析，还可以检测信号的振荡器异性等行为。总之，一种是基于概率测度下的奇异性，一种基于连续函数的连续性，分别来源于不同的数据应用，对于大分辨率的数据，两者的刻画能力相同，而对于小尺度的地学数据，盒子法的效果更优。

[1] Mandelbrot BB. Intermittent turbulence in self similar cascades: Divergence of high moments and dimension of the carrier [J]. Fluid. Mech., 1974, 62: 331.

[2] Cheng Q. Multifractality and spatial statistics [J]. Computers & Geosciences, 1999, 25(9): 949-961.

[3] Cheng Q, Agterberg FP. Comparison between two types of multifractal modeling [J]. Mathmatical Geoglogy, 1996, 28(8):1001-1016.

[4] Halsey TC, Jensen MH, Kadanoff LP. Fractal measures and their singularities: The characterization of strange sets [J]. Phys. Rev., 1986, 33(2): 1141-1151

[5] Arneodo A, Bacry E, Muzy JF. The thermodynamics of fractals revisited with wavelets [J]. Physica A, 1995, 213: 232-275.

[6] Schertzer D, Lovejoy S, eds. Non-linear variability in geophysics [M]. The Netherlands: Kluwcr Acad. Publ., Dordrecht, 1991.

[7] Parisi G., Frisch U. On the singularity structure of fully developed turbulence, in Turbulence and Predictability in Geophysical Fluid Dynamics [M], edited by M. Ghil, R. Benzi, and G. Parisi, New York: Elsevier,1985.

[8] Muzy JF, Bacry E, Arneodo A.. Wavelets and multifractal formalism for singular signals-application to turbulent data [J]. Physical Review Letters, 1991, 67(25):3515-3518.

[9] Mallat S, Hwang WL. Singularity detection and processing with wavelets [J]. IEEE Trans. Inf. Theory, 1992, 38, 617-643.

[10] Jaffard S. Multifractal formalism for functions [J]. SIAM J. Math. Anal., 1997, 28(4): 944-998.

[11] Cheng QM, Agterberg FP, Ballantyne SB. the separation of geochemical anomalies from background by fractal methods [J]. Journal of geochemical exploration, 1994, 51(2):109-130.

[12] 郭科，施泽兴，唐菊兴等.用多重分形研究元素的共生组合.电子科技大学学报,2004,33(2)：221-224.

[13] Zheng Z, Mao H, Cheng QM. Fractal geometry of element distribution on mineral surfaces [J]. mathematical of geology, 2001, 33(2): 217-228.

[14] Dojnow P. Multifractal analysis of amplitude and phase components of EEG-based analytical signals [J]. Comptes Rendus De L Academic Bulgare Des Sciences, 2007, 60(10):1071-1076.

[15] Khalil A, Grant GL, Caddle Lb, et al. Chromosome territories have a highly nonspherical morphology and nonrandom positioning [J]. Chromosome Research, 2007, 15(7):899-916.

[16] Evertsz CJG., Mandelbrot BB. Multifractal measures, In: Peitgen, H.O., Jurgens, H., Saupe, D. (Eds.), Chaos and Fractals. Springer [M], New York: Springer, 1992.

[17] Wendt H, Roux SG., Jaffard S, et al. Wavelet leaders and bootstrap for multifractal analysis of images [J]. Signal Processing, 2008, 89(6): 1100-1114.

[18] De Wijs, HJ, Statistics of ore distribution [J], Geologic en Mijnbouw. 1951, 13 (8), 365-375.