数学教学要注重学习方式的转变

崔永红

（江阴职业技术教育中心校，江苏 江阴 214433）

建构主义认为：数学学习是一个主动建构的过程，对学生来说，获得知识需要经历对知识的再创造过程，学生学习数学的过程不是被动地吸收书本上的现成结论，而是亲自参与的充满丰富思维活动、经历实践和创新的过程。具体地说，学生从数学现实出发，在教师的帮助下，自己动手动脑做数学，通过观察、模仿、实验、猜想等手段收集材料，获得体验，并进行类比、分析、归纳，形成自己的数学知识结构。

一、彰显学生的主动性，变被动学习为主动学习

学生是学习的主人，数学学习离不开学生为主体的实践活动，课堂上，教师应给学生更多的自主学习的空间，让学生在教师的引导下独立地提出问题、分析问题和解决问题，在主动实践的过程中实现自我发展。

1.创设情境

上课伊始，教师用几何画板作出f1（x）=x2，f2（x）=2的图像，让学生观察图像，并相互交流，同学们积极性很高，纷纷提出了自己的看法，不少同学观察的结论很有价值，如f1（x）=x2的图像在y轴右边沿x轴上升并且关于y轴对称。教师趁机打铁，适时提问：

师：这两个图像有什么共同的特征？学生积极思考，或小组合作，或交流讨论。

要实现由被动学习为主动学习，教师要把学习内容巧妙地转化为问题情境，在学生心理上造成一种怀疑、困惑、焦虑，但又渴望探索、解决未知问题的心理，从而激发学生强烈的学习欲望，积极主动地投入学习。

2.适时铺垫

问题有些难度，教师适时做一些铺垫，让学生计算：

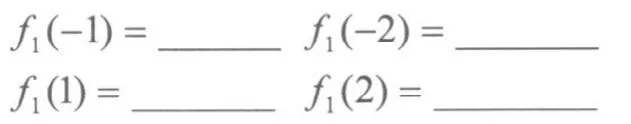
学生通过计算，由特殊到一般，很快得出了：f1（-x）=f1（x），f2（-x）=f2（x）。

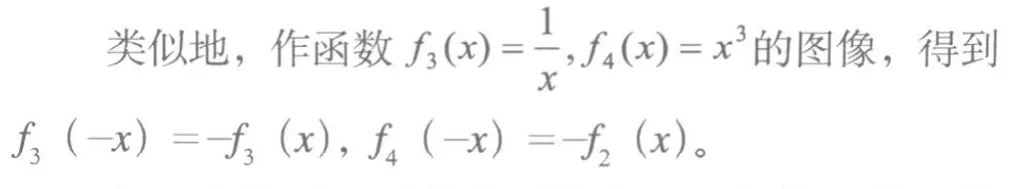
师：上述两个函数分别代表了两种特殊的函数——偶函数和奇函数。

3.构建概念

在教师指导下，让学生尝试给函数的奇偶性下一个定义：对于函数y=f（x）定义域内任一x，若f（-x）=f（x），则称函数y=f（x）为偶函数；

若，则称函数y= 为奇函数。

让学生自主构建概念，变“权威——服从”的课堂模式为“指导——参与”模式，变教师“带着知识走向学生”为“带着学生走向知识”，有利于形成和谐、民主、平等的师生关系，学生在这样的课堂氛围中，才能畅所欲言，各抒已见，主动地去获取知识，主动地去发现问题，才能由被动学习转变为主动学习。

4.理解概念

学生在自主探究的过程中，有时对概念的理解不够深刻，甚至会错误地理解概念，这时教师要为学生提供必要的帮助，为他们指明一条前进的方向。例如，学生对“奇偶函数的定义域必须关于原点对称”理解不深，教师可设计如下的教学方案，帮助学生理解。

师：判断下列区间是否关于原点对称。

（1）（-∞，＋∞）（2）［-1，1］（3）（-1，1］（4）（-∞，-1）∪［1，＋∞）

生：（1）（2）关于原点对称，（3）（4）不关于原点对称。

整个课堂上，学生不再是被动的接受者，而是主动的参与者、探索者，学生的自主性得到了充分的发挥。在教学中教师的主要任务不是把知识灌输给学生，而是把学习方法教给学生。

二、调动学生的积极性，变个别学习为合作学习

在自主探究过程中，教师应为学生提供广阔的空间，给予足够的时间，让学生主动参与到合作学习中去，从而调动他们的积极性。

例如，在学习了函数的奇偶性时，给出这样一道习题：判断函数y=（x-1）0的奇偶性。为了给学生一个相互合作的机会，笔者没有直接给出答案，而是让学生思考后各自说出自己的思路，再进行小组交流，答案错误的同学很快明白了错误的原因，为自己弄懂了一个新问题而兴奋不已，答案正确的同学更为自己的讲解而自豪，全班同学情绪高涨。

接着教师提问：既然存在既不是奇函数又不是偶函数的函数，那么是否存在既是奇函数又是偶函数的函数呢？

这一问，学生刚才那兴奋劲一下又被安静取代了，一阵深思之后，大家你看看我，我看看你，连平时善于回答问题的同学也在皱眉头。这时适时引导学生进行小组合作讨论与交流。

这样的安排，每个学生都有表现自己、展示才华的机会，课堂上同学们始终情绪高昂。小组合作学习不仅节省了时间，实现了能力的互补，而且很好地培养了学生的合作意识。

三、激发学生的创造性，变接受学习为探究学习

教师要把在课堂上激发出来的学习热情投入到具有创新意义的学习中去，为学生拓展创新学习的空间，让学生的创造潜能得以充分的发挥，以满足不同学生的发展需要。在学完了本节的内容之后，为了充分利用学生高涨的学习热情，将教学内容拓宽延伸，笔者没有直接讲解“f（x）=ax+b的奇偶性”，而是让学生合作探究，教师巡回指导或点拔，讨论的结果很快就出来了。

生甲：f（x）是非奇非偶函数。

生乙：应该讨论。

师：很好！怎样讨论呢？

生丙：当a≠0，b≠0时，f（x）是非奇非偶函数；当a≠0，b=0时，f（x）是奇函数；当a=0，b≠0时，f（x）是偶函数；当a=0，b=0时，f（x）既是奇函数又是偶函数。

学起于思，思源于疑。学生越是困惑，探究知识的欲望就越强烈，数学教学中只要抓住了学生的心理，抓住时机，教学效果就会事半功倍。当然在探究活动中，要正确处理好教与学的关系，在突出学生的主体地位的同时，不能忽视教师的指导，教师指导的原则是到位不越位，参谋不代谋，指导不指令，从而有效摒弃传统的“知识课堂”中那种忽视学生的主体地位，采用强制的“填鸭式”教学，学生缺少主观能动性，只是机械地记忆和接受知识的状况，转化为新课程所强调的学习数学过程不是被动吸收现成结论的过程，而是学生积极参与的充满丰富生活体验的活动过程，是实践与创新的过程。

［1］ 古德布罗菲.透视课堂［M］.中国轻工业出版社，2002.

［2］ 朱恒杰.新课程有效教学疑难问题操作性解读［M］.教育科学出版社，2008.

［3］ 方均斌.数学教学案例反思及延伸［M］.四川大学出版社，2009.