一种基于SUSAN算子和相位相关实现图像配准的算法

方 壮

(1.重庆大学 数理学院，重庆 400030；2.湖北民族学院 理学院，湖北 恩施 445000)

图像配准是将取自不同时间、不同角度的同一目标区域的两幅或多幅影像,在空间位置上对准.这些图像或者来自不同传感器，或者是由同一传感器在不同时刻获取.图像配准被广泛地应用在遥感图像、医学影像、三维重构、机器视觉等诸多领域中[1]，图像配准方法的研究一直是国内外的研究热点，到目前为止，出现了很多图像配准方法，它们大体可以分为两类：一类是基于各类变换如Fourier变换、小波变换等，在变换域中实现图像的配准；另一类是基于灰度图像在空间域实现图像的配准.

1 基于变换域的图像配准方法

傅里叶变换方法是基于变换域的图像配准方法中最主要的方法.依据傅里叶变换的平移性质，即同一幅图像无论如何平移，其对应的频域幅值和原始图像都是完全一样的，而发生变化的只是它们的相位.以此为依据的相位相关方法能够较好的实现图像在频率域中的配准，其主要原理可简述如下：

数字图像f(x,y)可以认为是二维离散信号构成的M×N矩阵，其傅里叶变换定义为:

其中u=0,1,…,M-1；v=0,1,…,N-1称为空域频率.

相应的傅里叶逆变换为:

其中x=0,1,…,M-1；y=0,1,…,N-1.

设同一场景两幅图像f(x,y),g(x,y)，f(x,y)是参考图像，g(x,y)是f(x,y)平移(x0,y0)后的位移图像，两者的关系可以写成:

g(x,y)=f(x-x0,y-y0)

令F(u,v)，G(u,v)分别是f(x,y),g(x,y)的傅里叶变换，则有:

G(u,v)=e-j2π(ux0+vy0)F(u,v)

即经过平移后的图像其傅里叶变换有相同的振幅，但存在相位上的差异，通过计算两幅图像的互功率谱来得到相位差，互功率谱定义为:

其中，F*是F的复共轭，由于傅里叶变换的平移理论保证了互功率谱的相位差与图像之间的相位差相等，对cp(u,v)取傅里叶逆变换，它在(x0,y0)处为冲击响应，因此在匹配点处可以得到傅里叶的逆变换峰值，进而确定图像之间的相位差(x0,y0).近来，文献[2]提出了基于梯度相位相关的自动图像配准方法，该方法有较强的抗噪能力，并能很精确的确定(x0,y0)，对于有旋转的情形，文献[3]通过极坐标变换，也能够求出旋转角度.基于梯度的相位相关方法能够较好解决整个图像的平移和旋转问题，但这一方法受限于傅里叶变换的平移不变性质，要求待配准图像g(x,y)和参考图像f(x,y)要有平移关系，而对于更一般的非平移的情形，比如g(x,y)是参考图像f(x,y)的一部分，或者图像g(x,y)和f(x,y)仅有一部分相互重叠，用该方法就不能实现图像的配准.因此相位相关方法虽然实现方法相对简单，但其缺点应用范围比较窄，不能满足实际中的条件要求.

2 基于灰度的图像配准方法

该方法的思想是建立这样一种假设：认为参考图像f(x,y)和待配准图像g(x,y)上的对应点及其周围区域具有相同或者相似的灰度.并以灰度相似为基础，定义相似性度量函数，然后通过一些匹配策略，找到一组最优或近似最优的几何变换参数，使得相似度函数最大，最终实现图像的配准.该方法的关键是定义度量函数，一种典型的的基于灰度的配准方法是Barnea[4]等人提出来的序贯相似检测算法，它定义了一种相似性度量准则:

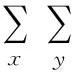
归一化准则为:

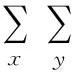
3 SUSAN角点检测算法

除了上述两种配准方法以外，角点检测实现图像的配准是现如今的一种比较常用的配准方法.角点没有准确的定义，一般认为在至少两个方向上图像灰度变化均较大的点是角点.角点具有信息量丰富、便于测量和表示、能够适应环境和光照变化等优点而受到了关注. 较早的角点检测算法有Moravec角点检测算法[5]，比较经典的有Harris角点检测算法[6]和SUSAN角点检测算法[7].SUSAN角点检测算法是由牛津大学的S M.Smith，J.M.Brady首先提出的，它主要用来计算图像中的角点特征的，因其运算效率高，角点检测准确，使其很适用于基于角点的图像配准.

SUSAN角点检测算法的主要原理.如图1所示，圆形区域内的每一个像素点的灰度值与中心像素点的灰度值比较，灰度值与中心像素点相近的点组成的区域称为USAN区域.从图1中可以看到，当核心点位于USAN区域内时，USAN区域面积最大，如图中e所示；当核心点位于直线或近似直线的边缘时，USAN区域的面积是最大时的一半，如图中b所示；当USAN区域面积最小时，核心点是角点，如图中a所示.

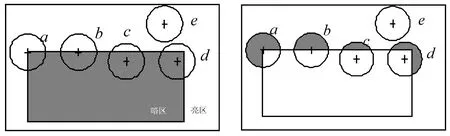
图1 不同位置的圆模板及所对应的USAN区域

SUSAN算法的数学描述：

SUSAN模板在图像上滑动，在每一个位置比较模板内各图像像素的灰度与模板核心的灰度：

其中，r是模板内除核之外的任意一点的位置，r0是图像中的核的位置，f(r)为r的灰度值，f(r0)为核的灰度值，t为阈值，主要用来控制生成角点的数量，C(r,r0)为灰度比较的结果.

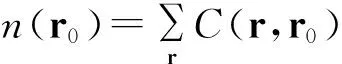
然后n(r0)与一个给定的阈值G进行比较：

n(r0)为反应函数，经过局部非极大值抑制之后确定为角点.

通过上述算法分析可以看出，SUSAN角点检测算法不需要进行梯度计算，这样就提高了算法的效率，实验还表明，该算法对局部噪声不敏感，抗噪能力强，检测角点的精确度较高， 适用于基于角点的图像配准.

4 本文算法及原理

同一目标区域在不同的成像条件下，其灰度关系保持一定的相关性，该目标区域作为参考图像f(x,y)中一部分，通过准确的角点检测，能够检测出该目标区域的角点，同时，该目标区域作为待配准图像g(x,y)的一部分，通过角点检测，也能够检测出该目标区域的角点，SUSAN角点检测算子能够保证两次检测的角点有很高的重复性度，即实际目标区域的同一个点在两次角点检测中都是角点的比率较高.以这些角点为中心，在f(x,y)和g(x,y)中取(2k+1)×(2k+1)的矩阵A和B，然后计算A和B的互功率谱cp(u,v)，最后计算cp(u,v)的傅里叶逆变换并求其峰值t，因为矩阵A和B是以同一目标区域的角点为中心，半径为k的(2k+1)×(2k+1)矩阵，其相关程度最高，反映在峰值上，此时t应为最大.

实际操作中，因为无法知道哪两个角点是准确对应的，需要分别求出参考图像f(x,y)和待配准图像g(x,y)的所有角点，按上述方法找到最大峰值两个角点为匹配的点，由此可以知道f(x,y)和g(x,y)的相对平移量，进而实现他们的配准.具体的算法步骤如下：

第1步，通过SUSAN角点检测算法检测参考图像f(x,y)和待配准图像g(x,y)的角点，此时可以得到各自图像的角点集 {P(xi,yi)|i=1,2,…,m}和{Q(xj,yj)|j=1,2,…，n}，m表示f(x,y)的角点个数，n表示g(x,y)的角点个数.

第2步，在各自图像中，以每个角点P(xi,yi)，Q(xj,yj)为中心，取半径为k的邻域，得到两列(2k+1)×(2k+1)的矩阵Ai(i=1,2,…,m)和Bj(j=1,2,…,n).

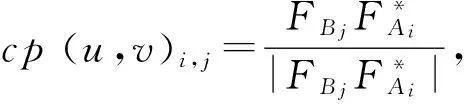
第4步，计算cp(u,v)i,j傅里叶逆变换icp(u,v)i,j(i=1,2,…,m；j=1,2,…,n).

第5步，计算icp(u,v)i,j的峰值Mi,j(i=1,2,…,m；j=1,2,…,n).在所有的峰值Mi,j中，最大峰值Ms,t对应的两个角点P(xs,ys)和Q(xt,yt)是匹配的，此时只要计算他们的坐标差就可以得到平移量.

在本算法中，唯一的参数是邻域半径k的大小，多次重复实验表明，k的范围在20～30之间能够有较好的配准效果.在k确定的情况下，输入参考图像和待配准图像便可以实现两幅图像的自动配准.

5 实验结果及结论

在Matlab环境中，以Lena384×384图像为基础图像(图2a)，加上随机噪声并且平移后得到的图像为模拟参考图像f(x,y)(图2b)，在Lena图像中任取一部分为待配准图像g(x,y)(图2c)，按下述方法进行独立实验，每个实验均独立重复10次，噪声强度一栏的数值以10次实验的理论值和实际值完全相符为准，实验结果见表1，配准后的图像见图2d.

表1 不同噪声下的配准结果

图2 配准结果

通过图2可以看出，当待配准图像是参考图像的一部分或这两幅图像只有一部分重叠时，本算法依然能很好地将它们配准，这就摆脱基于傅里叶变换的相位相关法对平移的限制.从表1中可以看出，本文提出的算法对噪声有很好的鲁棒性.事实上，通过大量的实验还可以发现，对于参考图像及待配准图像均有混合噪声和灰度变化时，本算法也能很好地实现两幅图像的配准.如实验结果所示，一幅先受到强度为0.05的Salt & pepper噪声影响，然后灰度值增加50，最后受到强度为0.05的Gaussian噪声影响后得到的参考图像(图2(e))域另一幅受到了强度为0.02的Salt & pepper噪声影响后得到的待配准图像(图2(f))，通过本算法配准后得到的结果如图2(g)，从图2(g)中可以看出，配准效果是十分理想的.

[1]冈萨雷斯.数字图像处理[M].北京:电子工业出版社，2003.

[2]甘亚莉，涂丹，李国辉.基于梯度相位相关的自动图像配准方法[J].微电子学与计算机，2007，24(7):1-3.

[3]甘亚莉，涂丹，李国辉.频率域基于梯度预处理的互相关图像配准方法[J].计算机工程与应用，2007，43(6)：24-26.

[4]S H F,Barnea D I.A class of algorithms for digital image registration[J].IEEE Transactions on Computers．1976，C-21(2)：179-186.

[5]Moravec H P. Towards automatic visual obstacle avoidance[C]//Proceedings of the 5thInternational Joint Conference on Artificial Intelligence，1977:584.

[6]Harrios C G,Stephens M.A combined corner and edge detector[C]//In 4thAlvey Uision Conference,1988:147-151.

[7]Smith M，Brady J M．SUSAN-A New Approach to Low Level Image Processing[J]．International Journal of Computer Vision,1997，23(1)：45-78.