Vander Waals势能问题不变积分保持算法研究

马大柱

(湖北民族学院 理学院，湖北 恩施 445000)

可靠的数值方法是非线性研究的基础.由于传统低阶数值算法如四阶龙格库塔法(RK4)本身的截断误差较大，高阶算法引入了人工耗散等因素，而相对热门的辛算法应用有限，所以寻找合适的数值计算方法成为当前非线性工作研究的热点问题.

自1971年Nacozy[1]提出流形改正方法以来，基于流形改正原理相继提出了一系列的不变积分保持算法.Vander Waals势能问题[2]存在两个稳定积分，为改正数值误差，可同时稳定两个或者其中一个积分.基于这种考虑，采用Ma[3]设计的速度因子方法稳定其能量积分，以及Zhong[4]构造的最小二乘法速度因子改正方法同时稳定两个积分.通过数值实验比较两种稳定方法优劣，推荐适用算法，力图避免数值误差产生的混沌.

1 不变积分保持算法

对一含有m个运动积分的微分动力系统：φi(x)=ci(i=1,2，…,m)，这里x为状态矢量，可分别代表坐标r和速度V，ci为运动常数.理想状态下有：

εi(x)=φ(x)-ci=0

(1)

由于数值误差的存在，往往在实际计算中εi≠0[5].为消除数值误差的影响，可选择两种方式，一种是构造高阶算法，但由于其引入人工耗散，不是理想的方案.另外一种就是改造低阶算法，如各种流形改正思想，也是目前通用的方案.

1.1 速度因子方法

Ma[3]在Nacozy流形改正原理的基础上，提出对速度分量可作如下形式的变换：

v*=s·v

(2)

式中v*和v分别代表速度真实值和数值解，s是标度因子.将式(2)代入到含标准积分值的表达式中，即可求出标度因子，此方法称之为速度因子方法.此方法对系统只要求含有一个积分即可.当然，还有很多其它的构造方式，此处不一一列举.

1.2 两个积分保持算法

若系统存在两个孤立积分，除采用以上的方法稳定一个积分外，还可以对两个积分同时稳定.一类仍然利用流形改正方法[6]，即将两个积分H1和H2对坐标分量和速度分量的偏导数组成以下矩阵形式：

(3)

真实值与数值解之间满足关系：

r*=r+Δηx，v*=v+Δηv

(4)

而Δη的计算需从下式中获得：

Δη=-ET(EET)-1ε

(5)

另外一类就是最小二乘法速度因子改正方法[4].该方法利用到了最小二乘法原理，其构造方式类似于速度因子改正方法.即要求速度分量都乘以一改正因子λ，有v*=λv.误差函数φ(λ)的形式为：

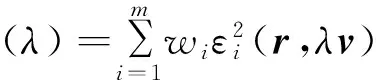
(6)

这里wi是权重因子.若误差函数最小，即要求φ′(λ)=0，可得出改正因子λ的具体表达式.

两类不同的改正方法以上已经详细介绍，其不同主要体现在构造方式上，尤其是速度因子方法构造极为简单，两个积分同时保持算法又存在两种不同形式，在实际运用中效果是否一样？实际模型将给出具体回答.

2 模型与计算结果分析

以标准的Vander Waals势能问题模型为例，其哈密顿形式为：

(7)

系统可积时要求B=15A.计算时为方便计，可令B=1.式(7)为该系统的一个积分，记为H1.此外系统还存在另外一个积分H2：

(8)

需注意的是式(8)是一对称形式，将x和y，px和py交换顺序，积分并无改变.获得这两个积分之后，将采用以上几种稳定方法投入实算，并进行比较.

数值比较之前，规定基本的数值积分方法为四阶龙格库塔法(RK4)，初始能量为E=1/12，庞加莱截面取(x,px)平面.首先关注无任何改正的情况，如图1(a)所示，截面上点的分布杂乱无章，轨道在截面上的投影非常模糊，轨迹极其粗糙，在平面下部尚能看出大致规律，上方却不能.这些都是由于RK4算法本身的误差较大引入的，实际轨道并不如此.再看单个稳定的情况，稳定之前需将稳定化程序代入到实际模型中去，获得改正因子.图1(b)即为能量积分稳定情况，与图1(a)相比，情况明显好很多，可看出轨道穿越情况，在截面上方的分布并非杂乱无章，只是点的分布略为粗糙，仍然不能完全清晰的反映轨道动力学特征.考虑将两个积分同时稳定的情况，计算过程与前相同，只是稳定化因子的求解稍显复杂，计算结果如图1(c)所示.从图中可以清晰的看到轨道在截面上的分布，与真实轨道最为接近，将数值误差的影响降低到最小.

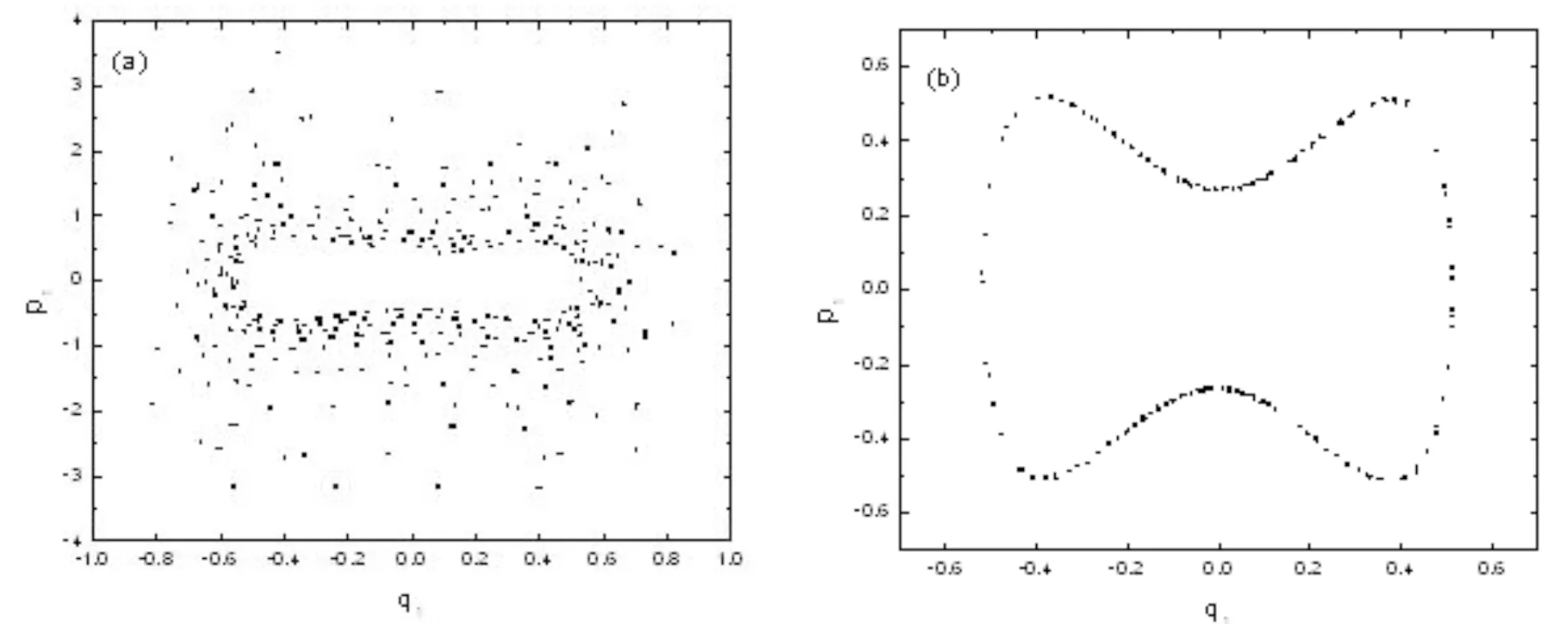
图2 (x,px)的相图

图1 (x,px)平面庞加莱截面图

通过以上数值实验可知，最小二乘法速度因子改正方法与速度因子方法相比，更能准确的保持系统的两个积分，真实反映相空间结构，最低限度的减少数值误差.如前所述，稳定两个积分还可以采用Nacozy提出的流形改正方法.数值实验的时候，也投入过实算，效果不太理想.究其原因，不难发现，该模型中第二个积分式(8)是一完全对称形式，其对坐标两个分量的导数完全相同，速度分量亦是如此.正是由于这样，导致该算法不再适用.

通过庞加莱截面比较了两种改正方法，对该模型的其它非线性性质的研究我们推荐采用最小二乘法速度因子改正方法.在这里一并做出该模型的相图，如图2所示.其中图2(a)是无改正时的情况，图2(b)是两个积分同时改正时的情况.通过(p1,q1)的相图，不难发现单纯的用RK4法计算得到的相图与实际情况相比误差极大.

3 结论

基于Vander Waals势能问题模型，通过庞加莱截面分析比较了单个积分改正方法与两个积分同时改正方法.相比较而言，速度因子方法虽然在一定程度上保持了单个积分，但是两个积分同时改正的最小二乘法速度因子方法却能更好的同时保持两个积分的数值精度，更加准确的反映了相空间几何动力学.另外，两个积分同时改正的流形改正方法不能处理含对称形式的积分，其应用有限.

[1]Nacozy P E.The use of integrals in numerical integtations of the n-body problem[J].Ap&SS，1971,14(11):40-51.

[2]Ganesan K, Lakshmanan M. Dynamics of atomic hydrogen in a generalized van der Waals potential[J].Phys Rev A,1990,42(10):3 490-3 497.

[3]Ma D Z. Velocity Scaling Method to Correct Individual Kepler Energies[J].New Astron,2008,13(5):216-223.

[4]Zhong S Y. Velocity Scale Factor with Least-squares Correction[J].Astrophys space sci,2009,324(1):31-40.

[5]Wu X. Comparison Among Correction Methods of Individual Kepler Energies in n-Body Simulations[J].A J,2007,133(6):2 643-2 653.

[6]Ma D Z. Velocity Corrections to Kepler Energy and Laplace Integral[J].Int J Mod Phys C,2008,19(9):1 411-1 424.