基于可拓距离的K近邻算法
2010-01-18向长城
向长城
(湖北民族学院 理学院,湖北 恩施 445000)
将物理或抽象对象的集合按照对象相似性进行分类的过程称为聚类.聚类分析的算法可以分为划分法(partitioning methods)、层次法(hierarchical methods)、基于密度的方法(density-based methods)、基于网格的方法(grid-based methods)、基于模型的方法(model-based methods).最近邻方法(K nearest neighbor,KNN)[1,2]工作原理是首先找到被分类对象在训练数据集中的K个最近的邻居,然后根据这些邻居的分类属性进行投票,将得出的预测值赋给被分类对象的分类属性.其优点在于分类准确率要高,无须事先知道属性值分布,自从KNN方法被提出以来,就在故障诊断、数据聚内、图像识别、文本分类[3,4]等领域得到广泛的应用.
相似性度量是KNN中的关键部分,传统上的相似性采用欧式距离等将各个属性取值的差异通过距离函数来计算.但对于同一属性内取值的差异怎样计算,欧式距离显然是不妥的.而由我国学者蔡文教授发明的可拓学中用来定量描述事物关联函数[5],不仅可以描述同一属性取值的差异,而且还可以提高聚类的准确率.在关联函数的基础上,设计了可拓距离,主要是用属性值与属性值区间描述的.本文利用可拓距离与KNN算法的思想,提出了可拓K近邻算法(extension K nearest neighbors,EKNN),并通过故障诊断与UCI的Iris数据集进了验证.
本文介绍了EKNN算法的设计,给出了新方法在故障诊断的过程和与其他算法在一些通用数据库分类准确率的比较结果,并对结论进行了分析与评价.
1 EKNN聚类算法
1.1 KNN算法
KNN基本思想是[3]:假定有n个类别为w1,w2,…,wn的样本集合,每类有标明类别的样本Ni个(i= 1,2,…,n),设样本的m个指标有构成一个m维特征空间,所有的样本点在这个m维特征空间里都有惟一的点与它对应.则对任何一个待识别的样本x=
(1)
通过构造距离公式(1),可以找到样本x的k个近邻.
又设这N个样本中,来自w1类的样本有N1个,来自w2类的样本有N2个,…,来自wn类的样本有Nn个.则对于一待分类的查询实例x,使用KNN进行分类的具体步骤是:
首先在训练样本数据集中选出最接近x的K个实例,并用x1,x2,…,xk表示,设k1,k2,…,kn分别是k个近邻中属于类w1,w2,…,wn的样本数.
定义序偶对
(2)
其中,若a=b,则σ(a,b)=1,否则σ(a,b)=0.
1.2 EKNN判别分析方法
可拓学是我国学者蔡文教授为解决不相容问题于1983年提出的一种方法,用形式化的语言对系统进行的定性和定量描述,其基于区间和点的关联函数的提出,为模式识别和模式分类提出了新的方法和思想.该算法首先按照样本的指标或者维数建立物元模型:
(3)
其中aj(x)为样本物元Sx的第j个指标Ij的值,j=1,2,…,m.
其次将N个向量xj(j=1,2,…,N)划分为n个组w1,w2,…,wn,又设这N个组中,来自w1类的样本有N1个,来自w2类的样本有N2个,…,来自wn类的样本有Nn个.并求每组的中心,使得相似性(或距离)指标的价值函数(目标函数)达到最小.其函数采用式(1)欧式距离.
计算该类别的中心物元为建立:
(4)
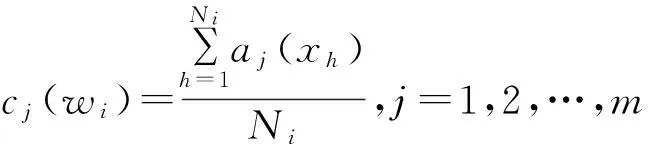
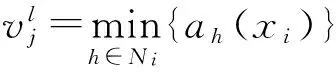
(5)
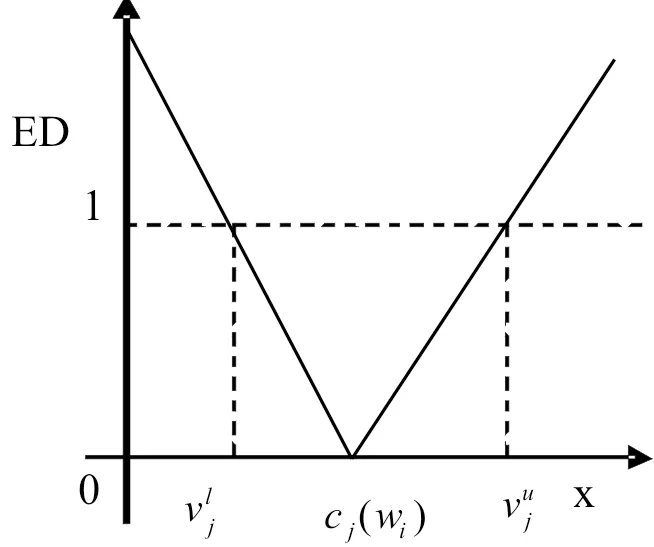
图1 一维可拓距离函数
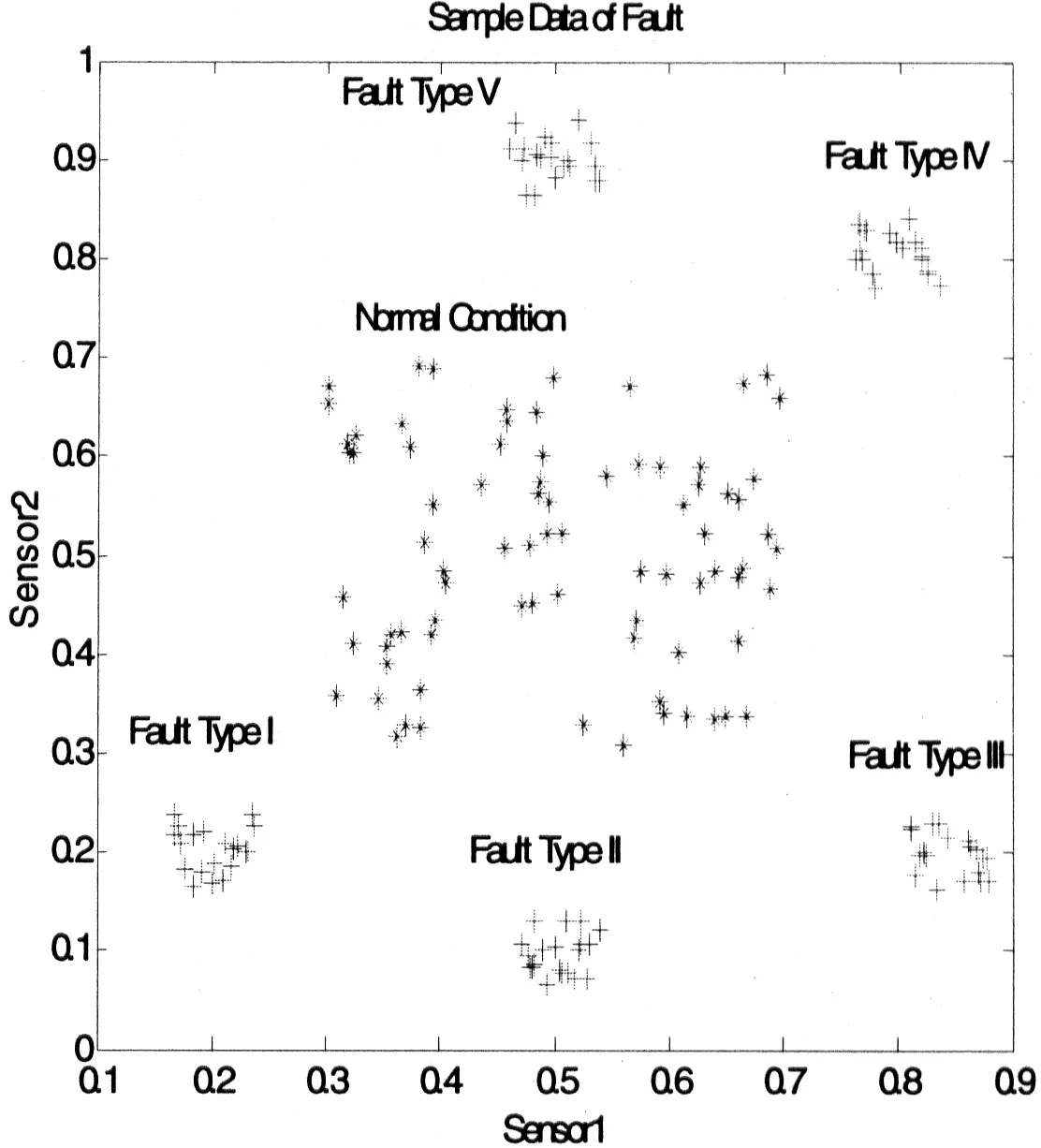
图2 180对传感器数据
可拓距离函数定义为:
(6)
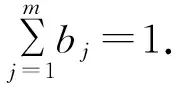
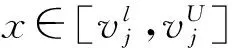
按照可拓距离值的大小从小到大对相应类别的进行排序,根据阈值σ选取最临近的K个类别.如果所有EDi≤σ(i=1,2,…,n)只有K′个,并且K≥K′,则令K=K′.
根据式(2)计算f(x).那个类别的个数越多,则样本点是该类.
2 实验验证
2.1 故障诊断
在本节用EKNN算法对故障进行识别.其样本数据集如图2所示,采用只有两个传感器的系统,来描述五个故障状态和正常状态.这6类数据分别代表了系统5个故障类型状态和正常状态,建立类别物元分别为:
其每个类别的中心物元通过计算可以得到:
通过采集测试物元并对其分类,建立测试物元分别为:
其中xi(i=1,2,…,6)为检策样本点,在图3中用“☆”标记.
以ND、FD1、FD2、FD3、FD4、FD5分别表示相关测试物元与正常类别、5个故障类别的可拓距离.根据式(6)和故障诊断的实际要求,取σ=3,K=3,其结果表1.

图3 样本数据和测试数据分布图
表1测试物元可拓距离表
Tab.1 Testing matter element ED table
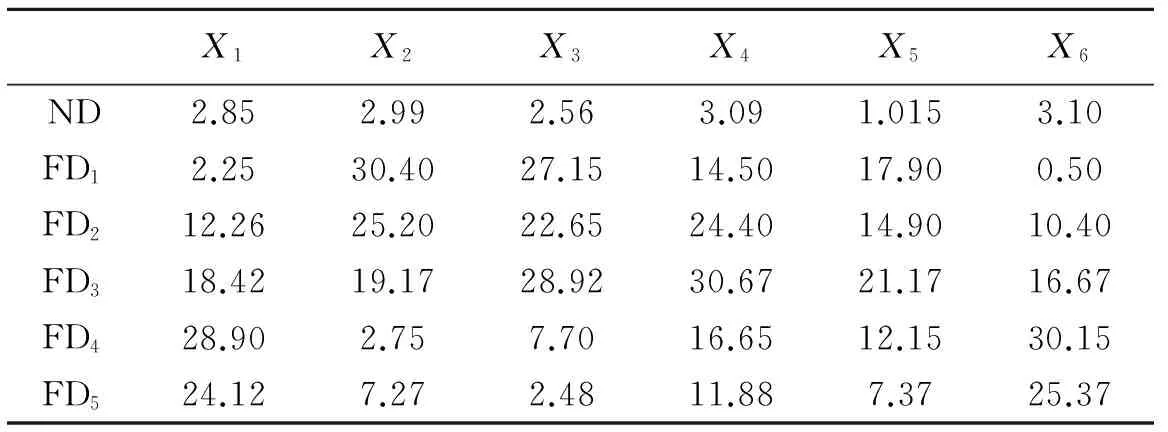
X1X2X3X4X5X6ND2.852.992.563.091.0153.10FD12.2530.4027.1514.5017.900.50FD212.2625.2022.6524.4014.9010.40FD318.4219.1728.9230.6721.1716.67FD428.902.757.7016.6512.1530.15FD524.127.272.4811.887.3725.37
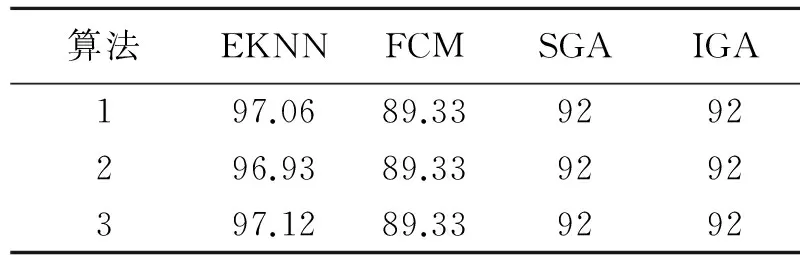
表2 各类算法分类正确率比较表
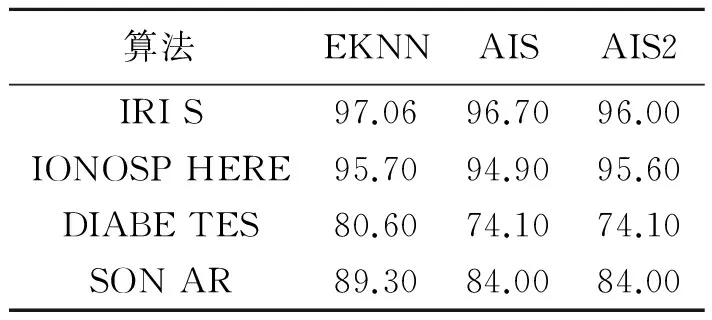
表3 不同数据集分类成功率
在表1中,第一列所表示物元,其可拓距离阈值取为σ=3,且3>ND>FD1,所以K=2,由式(2)可知,样本点x1属于第一种故障类型.同理可知,x2,x3,x5,x6分别为第四类、第五类、正常和第二类故障类型,其中第四类样本点,ND、FD1、FD2、FD3、FD4、FD5均大于3,此时可知该样本点不属于已有的类别.分析其原因可知,系统在原来基础上已经发生了新的变化,可能是系统新的故障类型出现.此时需要对该类型故障进行学习和记忆,并且作为一种新的故障类别加入到故障诊断数据库中.
2.2 数据集聚类
Fisher的Iris植物样本数据共有150个样本,每个样本均为4维sepal length,sepal width,petal length and petal width模式向量,代表植物的4种特征数据.其中Iris-setosa、Iris-virginica,Iris-versicolor各50个样本组成三类数据.表2为分别用遗传算法(SGA)[6]、模糊C-均值算法(FCM)[6],免疫遗传算法(IGA)[6]做了3次实验与EKNN算法的比较.
表3为数据集合IRIS与其他三个数据集DIABETES[7]、IONOSPHERE[7]、SONAR[7]分别用EKNN与AIS[8],AIS2[8]的比较.
通过表2可知,本文EKNN算法的分类准确率较SGA,FCM,IGA算法更高,其中FCM准确率最低,在表3中发现EKNN算法在性能上优越于AIS,AIS2法,尤其在维数较大时,其准确率更高.
3 结论
通过上述两个实例说明,本文构造的基于可拓距离的K近邻算法在数据聚类和故障诊断方面分类准确率高,对于算法运算速度问题研究和改进,是下一步的重点工作.
[1]Thierry Denoeux.A k-Nearest Neighbor Classification Rule Based on Dempster-Shafer Theory[J].IEEE Trans,on Systems Man and Cybernetics,1995,25(5):804-813.
[2]Lalla Meriem Zouhalm,Thierry Denoeux.An Evidence-Theoretic k2NN Rule with Parameter Optimization[J].IEEE Trans,on Systems Man and Cybernetics,1998,28(2):263-271.
[3] Pan J S,Qiao Y L,Sun S H.A fast K nearest neighbors classification algorithm[J].IEICE Trans Fundamentals,2004,E87-A(4):961-963.
[4]朱大奇,于盛林.基于DS证据理论的数据融合算法及其在电路故障诊断中的应用[J].电子学报,2002,30(2):221-223.
[5]蔡文,杨春燕,林伟初.可拓工程方法[M].北京:科学出版社,2000:1-50.
[6]时念云,蒋红芬.基于免疫单亲遗传和模糊C均值的聚类算法[J].控制工程,2006,13(2):158-160.
[7]Machine Learning Repository,Center for Marchine Learning and Intelligent Sytem[OL].[1993-03-08].http://archive.ics.uci.edu/ml/machire-learning-databases/iris.
[8]A Watkins and Timmis J. Artificial immune recognition system (airs):Revisions and renements[C]//Timmis and P.J.Benltey.1st International Conference on Articial Immune Systems.kent,UK:University of Kent at Canter Bury Printing Unit,2002:173-181.
