因子分析在学生成绩影响因素调查结果中的应用
2010-01-18张喜娟丁钊鹏
张喜娟,丁钊鹏
(北京联合大学 商务学院,北京 100025)
因子分析在学生成绩影响因素调查结果中的应用
张喜娟,丁钊鹏
(北京联合大学 商务学院,北京 100025)
因子分析基本思想是通过对多个原始变量提取主成分,经过正交旋转,可以找出主要的独立影响因素。通过对学生的多因素多样本问卷调查,将因子分析应用于教育教学数据分析之中,从而找出影响学生学习成绩的主要原因,为进一步的教育教学改革提供了一定的理论依据。
主成分;因子分析;正交旋转
1 因子分析的基本原理
在实践中,往往收集到的数据是多指标的。各指标之间通常不是独立的,或多或少存在着一定程度的关系。因子分析的目的是通过少数几个变量去描述这众多变量间的协方差关系。这少数几个变量是潜在的,但不能观察,我们称之为因子。
在所收集到的众多变量中,必定存在某些是高度相关的,把这些高度相关的变量组成各组。这样,同一组内变量具有高度相关,而与其他的各组变量却只有较小的相关或是不相关。这些组内高度相关的变量可以设想是一个共同的东西在影响着它们而导致高度相关。这个共同的东西称之为公共因子。如前所述,这些公共因子是潜在但不能观测的。
因子分析法是利用著名的统计软件 SPSS,对收集到的大量数据进行统计分析,用较少的相互独立的因子变量代替原来变量的大部分信息。
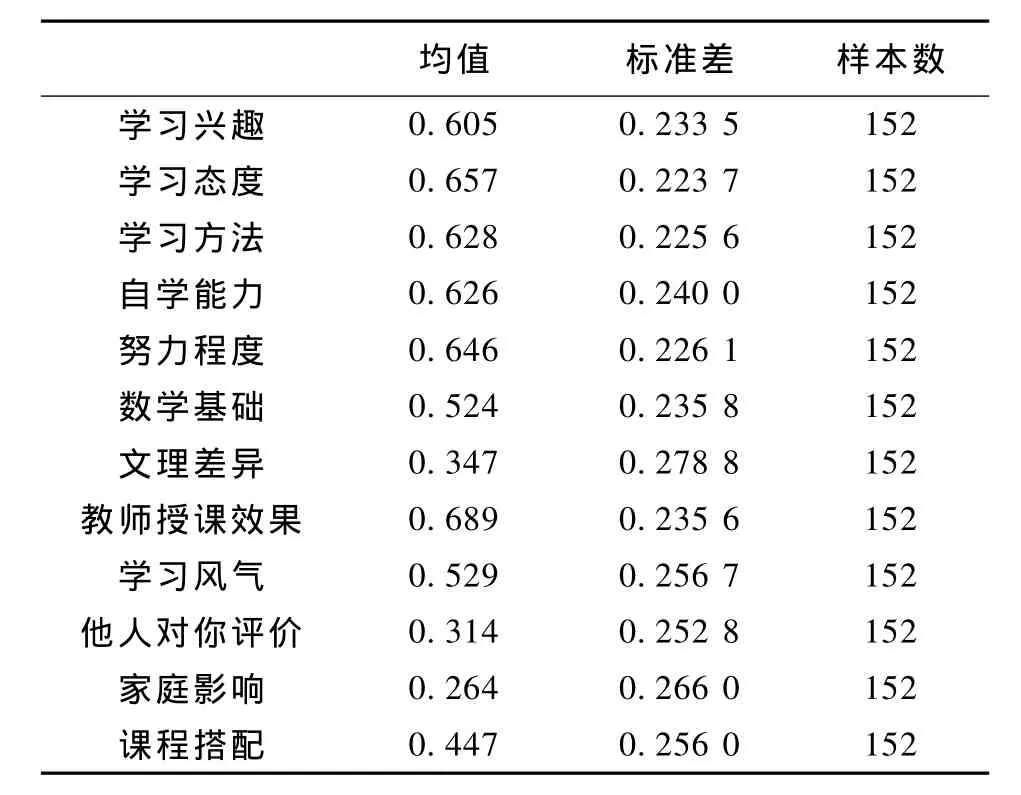
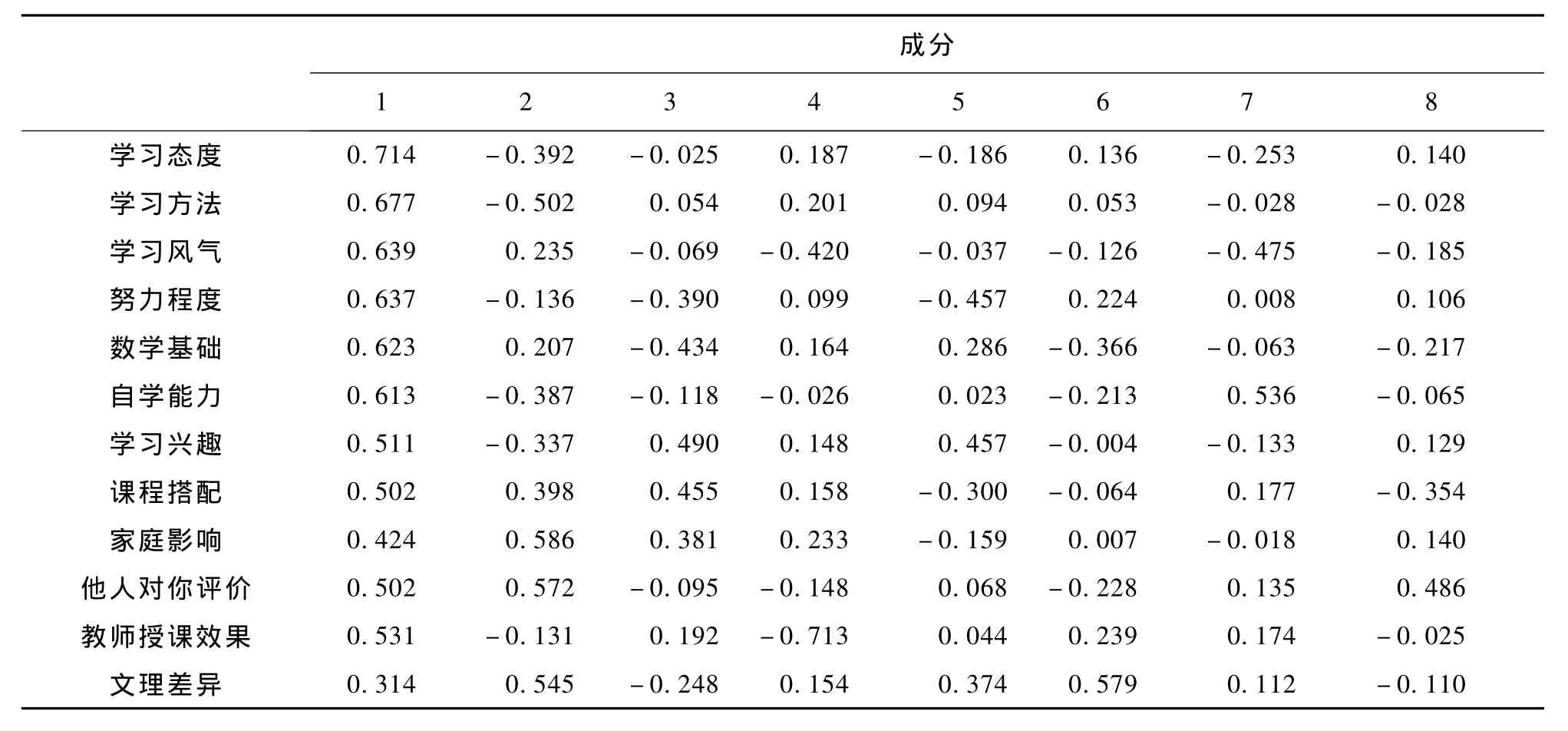
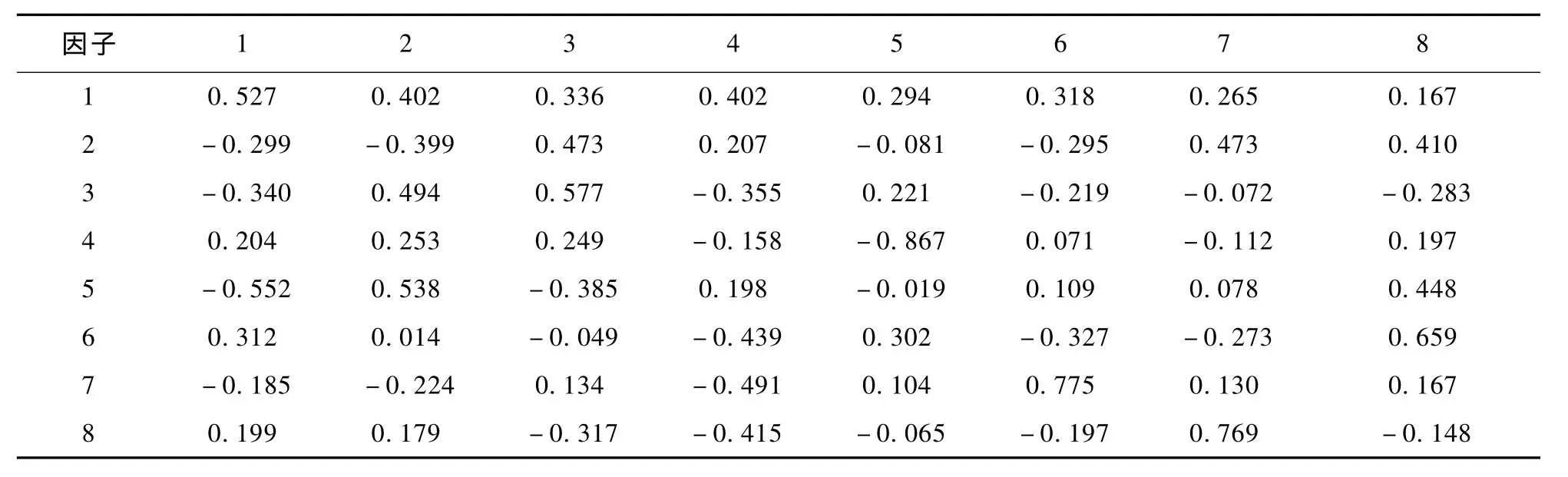
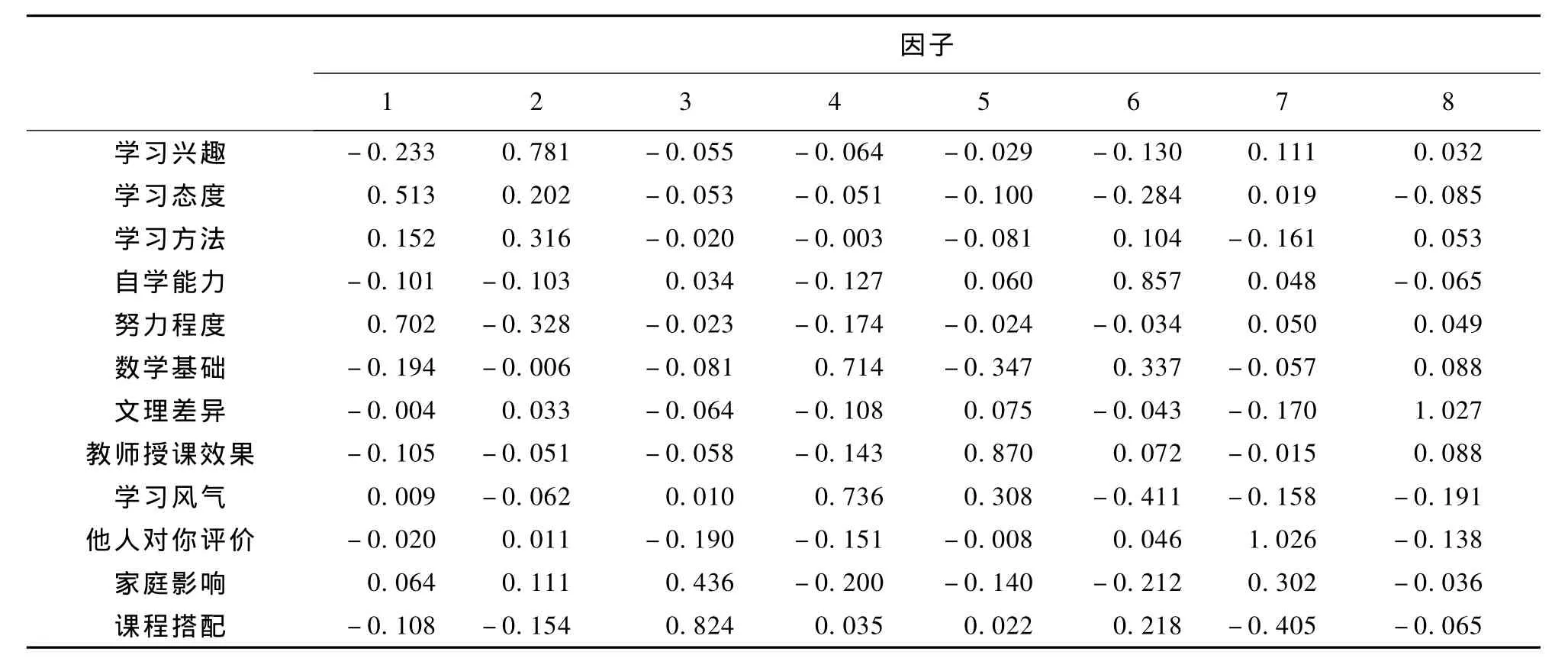
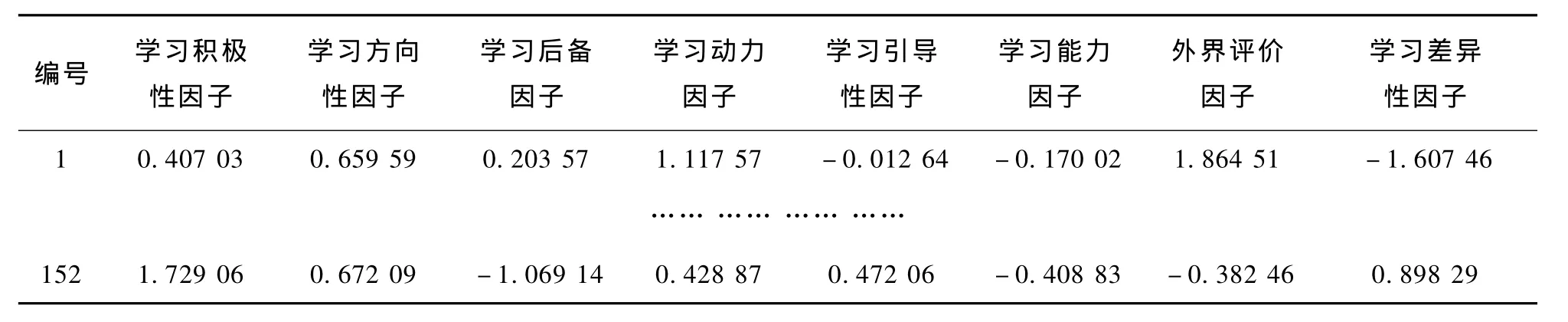
设有样本容量为 n的 p个变量,通过变换,将原变量Xi转换成主成分(用F表示)。主成分是原变量的线性组合,且具有正交特征,即将X1,X2,…,Xp综合成 k(k 这样确定的综合变量 F1,F2,…,Fk分别称作原变量的第 1、第 2、…、第 k个主成分,且 F1,F2,…,Fk在总方差中占的比例依次递减。 下面,我们就以学生成绩影响因素调查为例,阐述因子分析法在具体事例中的应用。 表1 观测数据 影响学生学习效果的因素错综复杂,本文从学习兴趣、学习态度、学习方法、自学能力、努力程度、数学基础、文理差异、教师授课效果、学习风气、他人评价、家庭影响、课程搭配等12个方面进行了问卷调查和严谨的统计分析。 为了调查影响学生成绩的主次因素,我们对上述可能的12个影响因素做出一张调查表,进行全面调研。每种因素从0~1依次分为6个等级,分别是0/0.2/0.4/0.6/0.8/1,所选影响因素分数越高,则代表学生认为此项因素对学习的影响越大。从所得的调查表结果中剔除一些明显的极端值,共得到152组观测数据。 首先看一下各变量的描述性统计量(数学期望和标准差),结果如表2所示。 表2 数学期望和标准差 各因素的标准差大体一致,说明离散程度(对各因素认同的离差)大体一致,而其中均值比较大的依次有教师授课效果(0.689)、学习态度(0.657)、努力程度(0.646)、学习方法(0.628)、自学能力(0.626)。但是,调查表中的各变量往往不是独立存在的,各变量之间总是或多或少地存在相关关系,比如说学习方法与自学能力之间一般就是相辅相成的,自学能力强的同学往往能摸索出一套较好的学习方法,学习方法优良的同学其自学能力自然也更强一些。从上面的调查表中,我们不妨对学习方法与自学能力进行Pearson correlations相关分析,可以得到这两个变量之间的相关系数为0.515。结果说明,仅就以上的描述性统计量得出教师授课效果是学生认为的第一影响因素的结论(因其均值最大)还言之过早。 目前,比较理想的变量降维的方法就是主成分分析与因子分析。这两种方法同时可以用较少的综合性指标分别综合存在于各变量中的各类信息。在这里,我们采用SPSS for Windows社会科学统计软件包,通过FACTOR过程进行因子分析。 在FACTOR过程中,选取学习兴趣等上述12个变量作为分析变量,选择Principal components主成分分析法,初步结果如表3所示。 既然有12个变量,自然就有12个成分(Component),位于上表第1列,在第2列Initial Eigenvalues中列出了各成分的特征方程的根,它是确定主成分数目之根据。这些特征值从大到小依次排列,根据方差的定义,第i个成分的方差是总方差在各成分上从新分配后在第i个成分上的分配结果,它恒等于第i个成分的特征值。在Initial Eigenvalues列同时也列出了各成分的贡献率(%of Variance)与累积贡献率(Cumulative%),它们表示了各成分能包含总信息的百分比和累积百分比。在此,我们选取12个主成分中的前8个作为主成分,这8个成分能解释原数据当中87.932%的信息。从下面的Scree Plot碎石图当中(见图1),也能看出各成分所包含信息之大小。表4中列出了成分矩阵,可以由它写出每个原始变量的因子表达式,如: 学习态度=0.714F1+(-0.392)F2-0.025F3+0.187F4-0.186F5+0.136F6-0.253F7+0.140F8 上式的F1~F8正是上面提到的8个主成分Component,在此也称为共性因子,其前面的系数表示该因子对变量的影响程度,即变量在因子上的负荷。 为了给共性因子命名,通过Varimax方差最大旋转(一种正交旋转方法),可以得到表5的因子转换矩阵,由原来的8个共性因子通过此矩阵的旋转得到另外8个正交因子。 图1 碎石图 表3 主成分分析法 表4 成分矩阵 表5 因子转换矩阵 表6是旋转后的因子(主成分)矩阵,此表给出了旋转后的因子负荷矩阵,可以看出,经过旋转后,负荷系数已经明显地分化了。 第1个主成分对努力程度、学习态度有绝对值较大的正负荷系数,可称之为学习积极性因子,解释了原始信息中的14.754%; 第2个主成分对学习兴趣、学习方法有绝对值较大的正负荷系数,可称之为学习方向性因子,解释了原始信息中的12.812%; 第3个主成分对课程搭配、家庭影响有绝对值较大的正负荷系数,可称之为学习后备因子,解释了原始信息中的12.224%; 第4个主成分对数学基础、学习风气有绝对值较大的正负荷系数,可称之为学习动力因子,解释了原始信息中的10.778%; 第5个主成分对教师授课效果有绝对值较大的正负荷系数,可称之为学习引导性因子,解释了原始信息中的9.876%; 第6个主成分对自学能力有绝对值较大的正负荷系数,可称之为学习能力因子,解释了原始信息中的9.488%; 第7个主成分对他人对你评价有绝对值较大的正负荷系数,可称之为外界评价因子,解释了原始信息中的9.185%; 第8个主成分对文理差异有绝对值较大的正负荷系数,可称之为学习差异性因子,解释了原始信息中的8.814%。 从表6中可以写出每个原始变量的因子表达式,比如: 表7是有关因子得分的信息,可以根据因子得分系数和原始变量的标准化计算每个观测量的各因子得分数,可以写出旋转后的因子表达式,比如 在数据编辑窗口中,可以以新的变量保存因子得分信息,新的8个正交因子变量得分数据如表8所示。 通过 Hierarchical Cluster聚类分析,对观测量进行两类聚类,因观测量过多,细节就不在此罗列。 结果表明,在两类聚类中,唯有第113个观测量落在第2类,其他151个观测量均落在第1类,从而说明这152个观测量共性很大。 从分析的结果可以看出,影响学习成绩的首要因素是学习的积极性(努力程度和学习态度),其次是学习的方向性(学习兴趣、学习方法)。虽然课程搭配、家庭影响、数学基础、学习风气、教师授课效果、自学能力、他人评价、文理差异各个因素都依次有不同程度的影响,但是首要的问题是学生自身的努力程度、学习态度、学习兴趣和学习方法。 表6 因子(主成分)矩阵 表7 因子得分系数 表8 得分信息 [1] 何晓群.现代统计分析方法与应用[M].北京:中国人民大学出版社,1998:281-332. [2] 于秀林,任雪任.多元统计分析[M].北京:中国统计出版社,1999:154-197. [3] 卢纹岱.SPSS for Windows统计分析[M].2版.北京:电子工业出版社,2002. [4] 赵新.层次分析法在教学质量综合评价中的应用[J].宁夏医学院学报,2002,24(2):155-156. [5] 杨德芹.教学质量评价模型及案例分析应用研究[D].武汉:华中师范大学,2008. The Application of Factor Analysis to a Study of Student’s Grades ZHANG Xi-juan,DING Zhao-peng Factor analysis obtains the main independent factors by principal components picking and orthogonal rotation from the original variables.This method analyzes the data obtained from the students’questionnaire survey and to find the main factor influencing their achievements. principal components;factor analysis;orthogonal rotation O 29 A 1005-0310(2010)01-0077-05 2009-11-26 张喜娟(1965—),女,河北省顺平县人,北京联合大学商务学院讲师,硕士,研究方向为数学教学与研究。 (责任编辑 李亚青)

2 样本及变量指标的选择
3 关于调查数据的因子分析


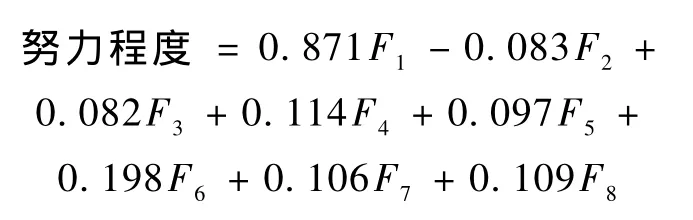

4 结论

(Business college of Beijing Union University,Beijing 10025,China)
