一类食饵捕食系统的持久生存性

陈红兵，何万生，刘晓君

(天水师范学院 数学与统计学院，甘肃 天水 741001)

一类食饵捕食系统的持久生存性

陈红兵，何万生，刘晓君

(天水师范学院 数学与统计学院，甘肃 天水 741001)

建立了一类3种群食饵捕食时滞系统，该系统由两类食饵和一类捕食者组成，并且能很好地反映捕食者与食饵之间的相互关系。接着研究了该系统解的存在性，该系统的解在满足初值条件下存在并且保持恒正。接着又研究了该系统的一致持久性问题，并给出该系统一致持久生存的充分条件和证明。最后举例论证了该结论的可行性。

食饵捕食系统;持久性;模型

许多文献都研究了两种群之间捕食与被捕食、相互竞争、互惠共存的模型，并且给出周期解存在性及全局渐近稳定性的充分条件。

［1］、［2］研究了一类恒化器数学模型

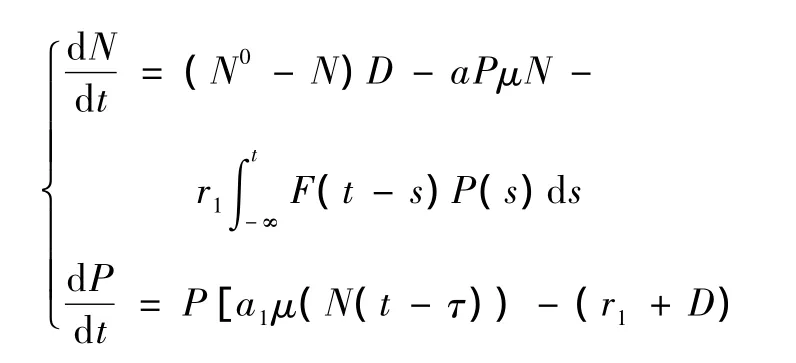
其中，N和P分别表示营养动物和浮游动物的浓度，并证明了该系统的一致持久性。

参考文献［3］研究了如下系统的持久性。

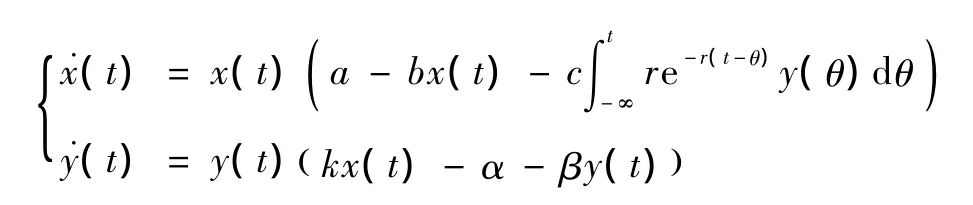
受上述文献的启发，本文我们建立如下系统。

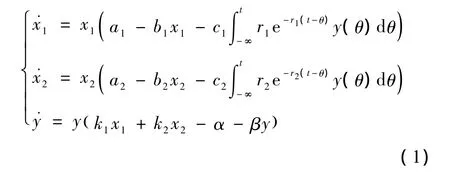
其中x1(t)、x2(t)表示t时刻食饵种群的密度，且x1(t)、x2(t)为相互独立的两种群。y(t)为 t时刻捕食者种群的密度，且满足 Lotka-Volterra模型。x1(t)、x2(t)分别满足Logistic模型。

1 一致持久性

引理 1［4］R3+是系统(1)的正向不变集。

证明 系统(1)等价于

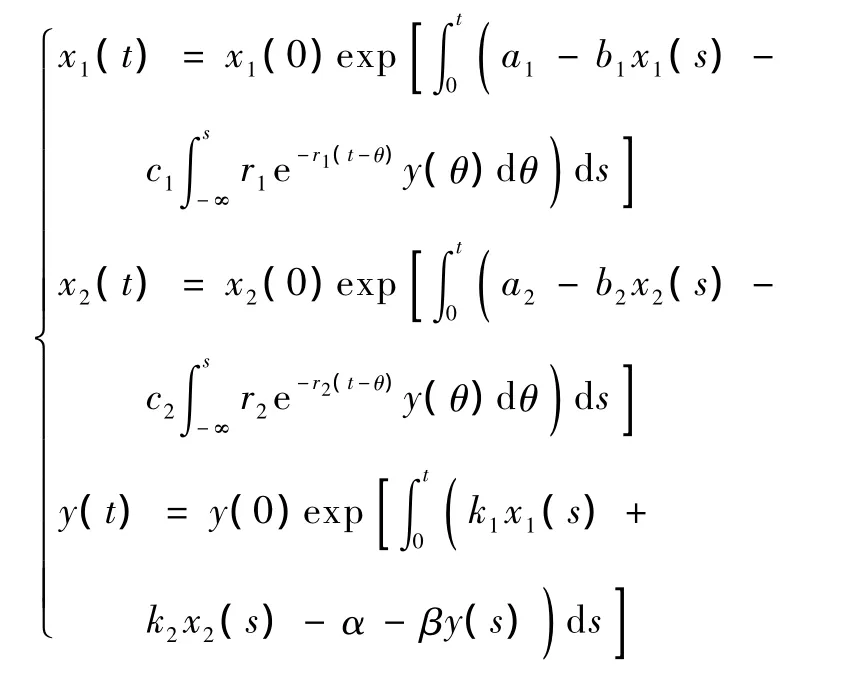
当 x1(0)= φ1(0)>0，x2(0)= φ2(0)>0，y(0)= ψ(0)>0时，必有 x1(t)>0，x2(t)>0，y(t)>0。

所以，该系统满足正初值的解保持恒正。

所以，R3+是系统(1)的正向不变集。

定义1［5］对于生态系统，如果存在一个紧区域DIntR3+，使得系统的任何满足初始条件的解(x1(t)、x2(t)、y(t))都最终进入并保留在紧区域D内，则称该系统是一致持久的。

定理1 设 (x1(t)、x2(t)、y(t))是生态系统满足初值条件的解，若满足下列条件

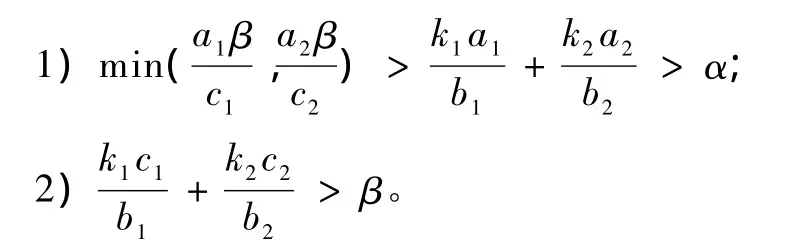
则系统是一致持久的。

证明 首先讨论上界

由引理1知R3+是系统(1)的正向不变集，则对于系统的任一正解(x1(t)、x2(t)、y(t))，由已知有(t)≤x1(t)(a1－b1x1(t))，则有

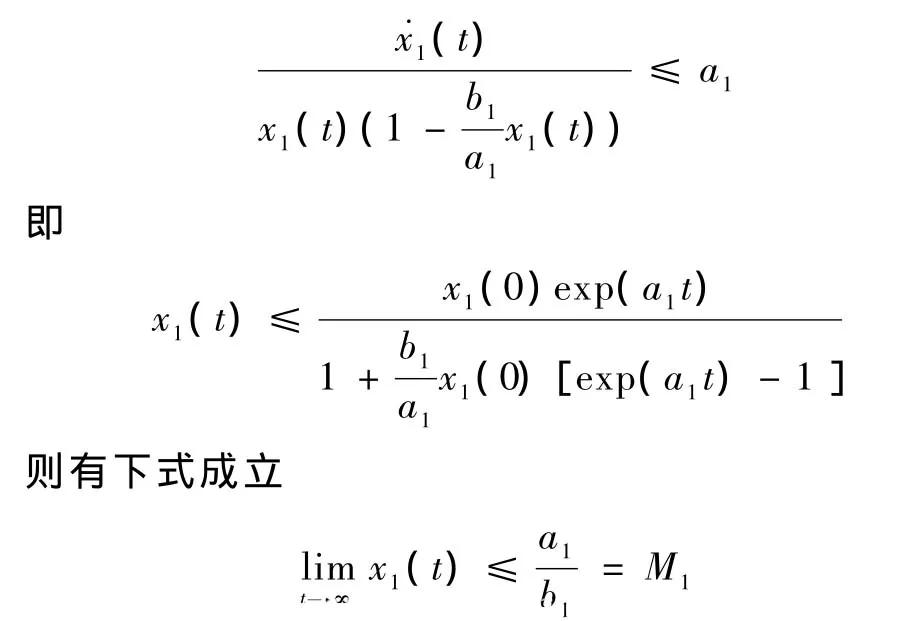
2 举例

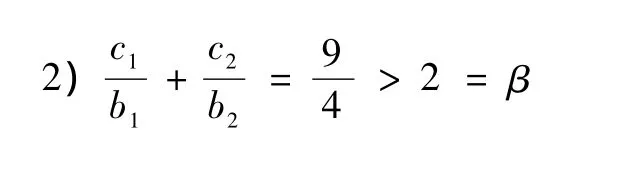
［参考文献］

［1］ Ruan Shigui.The dynamics of chemostat models［J］.Journal of Central China Normal University:Natural Sciences，1997，31(4):377－397.

［2］ 付桂芳，马万彪.由微生物方程描述的微生物连续培养动力系统［J］.微生物通报，2004，31(6):128－131.

［3］ 陈荣福，赵明.一类捕食者与被捕食者模型的持久性与稳定性［J］.生物数学学报，2008，23(2):289－294.

［4］ 孟新柱，董焕河，张宁.一类 Lotka－Volterra捕食 －竞争扩散系统的概周期解［J］.数学研究，2004，37(4):387－393.

［5］ Chen F D，Shi J L，Chen X X.Persistence and global stability for two－species nonautonomous predator－prey system with diffusion and time delay［J］.Annal ofDifferential Equation，2004 20(2):111 －117.

［6］ 徐建华.一类时滞积分方程概周期解的存在性［J］.系统科学与数学，2003，23(2):251－256.

The Persistence of a Predator-prey Model

CHEN Hong-bing，HE Wan-sheng，LIU Xiao-jun

(School of Mathematics and Statistics Tianshui Normal University，Tianshui Gansu 741001，China)

A new prey-predator system is proposed，which is constituted of two prey and one predator，and the prey-predator system is presented by this modle.Next，the existence of the positive solution for this system is studied.In addition，the persistence of this mode is given and proved.The example is given to illustrate the results.

prey-predator system;persistence;model

TP 13

A

1005-0310(2010)01-0065-02

2009－09－25

甘肃省自然科学基金项目(096RJZE106)

陈红兵(1983—)，女，甘肃省静宁人，天水师范学院助教，硕士，研究方向为应用微分方程。

(责任编辑 李亚青)