工程测量中新旧坐标转换的一种实现方法

赵小领

(山西省地质勘查局二一七地质队测量公司，山西 大同 037008)

工程测量中新旧坐标转换的一种实现方法

赵小领

(山西省地质勘查局二一七地质队测量公司，山西 大同 037008)

常规的测量坐标转换模型因采用确定的变换参数而导致坐标换算误差。将转换区域内各新旧坐标公共点视为精度均匀的离散点，通过计算区域重心坐标和坐标转换的初始参数，求取各公共点的坐标换算近似值及其改正数。在此基础上，根据公共点旧坐标与其改正数的对应关系，利用常规数字成图软件的离散函数插值功能，获取任意点的坐标换算改正数，实现新、旧坐标转换。实例应用表明，该法简便可行，换算精度高，是新旧测量坐标转换的有效方法。

工程测量；坐标转换；初始换算参数；坐标改正数

在工程测量和地籍测量中，经常要对现有的控制网或已有的测绘成果进行重测、补测或坐标纠正。[1、2]不同起始数据和不同测量条件下得到的测量结果会有所差别，通常不可能对已有旧坐标的全部点重测其新坐标，而是对旧坐标系中若干控制点进行重新测量，根据这些公共点的新、旧坐标建立坐标转换模型，将任意点旧坐标转换为新坐标。根据测量学理论，当新、旧坐标系的坐标原点和坐标轴夹角关系已知，或者新、旧边长比为常数时，可通过坐标轴旋转、平移和比例缩放，由平面坐标转换公式来实现坐标换算。[3、4]对于两个以上公共点的情形，可按最小二乘原理采用间接平差法确定新、旧坐标统一转换模型的参数；[5、6]但对于较大面积的换算区域或有多个公共点的情形，上述平面坐标转换的确定数学模型不能精确地反映新、旧坐标转换参数随位置变化的特征，导致坐标换算存在较大的模型误差。为此，将转换区域内各新、旧坐标公共点视为精度均匀的离散点，在计算区域重心坐标和初始换算参数的基础上，求取各公共点的坐标换算近似值及其改正数。根据公共点旧坐标与其改正数的对应关系，选择合适的改正数函数模型，[7、8]利用常规数字成图软件中的插值功能，[9]获取任意点的坐标换算改正数，实现新、旧坐标的高精度换算。

1 坐标转换模型

假设区域内包含n个公共点，其旧坐标xi，yi和新坐标Xi，Yi为已知，按下述步骤实现新、旧坐标的转换：

(1)计算旧、新坐标的重心坐标x0，y0，X0，Y0

(2)计算初始转换参数

通过坐标反算得旧、新坐标系中公共点i与其重心0的连线长度 l0－i，L0－i，重心 0 至公共点 i的方位角α0－i，α0－i及相应方位角之差。按下式计算初始长度比λ0；初始旋转角φ。及转换参数A，B。

(3)在旧坐标系中，计算各公共点相对于重心坐标x0，y0的坐标增量△xi，△yi及坐标增量的初步换算值η xi，η yi

(4)按下式计算初步坐标换算值X′i，Y′i及其改正数δXi，δYi

(5)根据n个公共点的旧坐标及相应的坐标换算改正数分别建立δX，δY的插值函数模型。

(5)式中插值函数的形式可根据公共点数量的多少来合理选择，如一次线性函数、二次多项式或样条函数等。其多项式系数可由公共点的已知坐标换算改正数 δXi，δYi按最小二乘法确定。在实际应用中，一般无需确定插值函数模型的具体表达式，可利用常规数字成图软件中已有的离散点插值功能，生成改正数δX，δY的插值模型或等值线图，自动获取任意非公共点 xj，yj的坐标换算改正数 δXj，δYj。

(6)在旧坐标系中按式(3)计算任意非公共点j相对于重心0的坐标增量△xi，△yi及坐标增量的初步换算值ηxj，ηyj，由下式计算非公共点的j新坐标Xj，Yj。

2 坐标换算的精度分析

分析式(6)可知，坐标换算误差主要由坐标增量换算值ηxi，ηyi的误差引起。将式(3)中第三、四两式分别对A，B，△x，△y求偏导得：

(7)式中

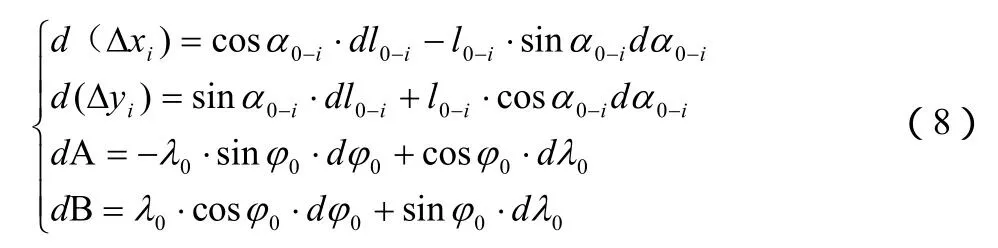
由于新、旧坐标换算的初始旋转角φ0一般接近于零，初始长度比λo接近于1。因此，可令A＝1，B＝0，d(λo)＝0，则式(8)可近似简化为：

将式(8)(9)代人式(7)并写为误差形式为[10]

(10)式表明，坐标换算误差主要由控制网本身的误差和计算初始旋转角的误差构成。因此，只要新旧坐标本身精度较高，即可获得高精度的坐标换算成果。

3 算例

已知某区域 8个控制点的旧坐标xi，yi与新坐标 Xi，Yi，见表1。

(1)将1～4点作为公共点，将5～8点视为待转换点进行坐标换算，并与实际坐标对比，以检测新、旧坐标换算的精度。由式①计算公共点1～4在旧、新坐标系的重心坐标x0，y0；X0，Y0，见表1。

(2)由式(2)计算初始转换参数，得：

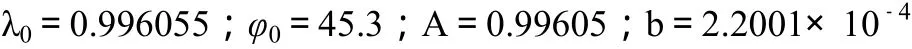
(3)由式(3)、(4)计算公共点1～4的初步坐标换算值X′i，Y′i及其改正数δXi，δYi，见表2 所示。

(4)由式(3)、(4)计算待换算点5～8坐标增量的初步换算值ηxj，ηyj和初步坐标换算值 x′j，Y′j，见表1 所示。

(5)利用常规的测绘专业软件获取非公共点坐标换算值的改正数δXj，δYj。本例在南方CASS5.0数字成图软件中，按规定的格式导人公共点坐标文件，xi，yi，δXi及xi，yi，δYi，将δXi或δYi视为“高程值”，由软件自动生成数字高程模型和改正数δX，δY的等值线图，在等值线图中根据待换算点的旧坐标xj，yj，直接获取改正数δXj，δYj，结果见表2。该法特别适用于公共点和待换算点数量较多的情形，由于无需设定和解算插值函数，使计算过程大为简化。

(6)按式(7)计算5～8的换算坐标。结果与实际坐标的偏差中误差为5.4 mm。表明上述坐标换算模型具有较高的精度。

4 结束语

本文采用了一种简便可行的方法实现新、旧测量坐标的换算。该法数学模型简单，适于计算机编程解算，借助常规数字成图软件可实现较大区域内多点新旧坐标的快速转换，在控制点本身测量精度较高的条件下，坐标换算误差很小，可满足工程测量要求。

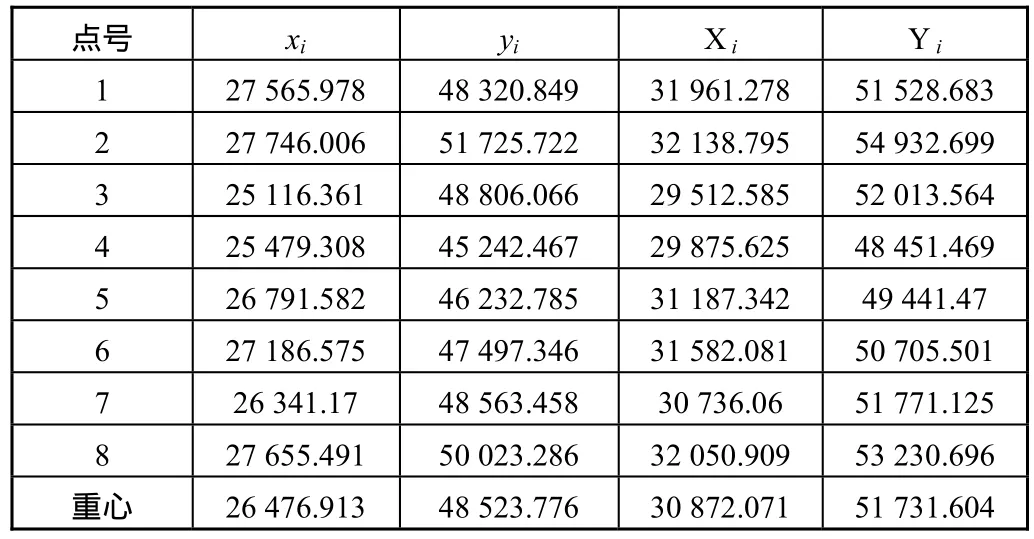
表1 已知点的旧坐标、新坐标与重心坐标

表2 初步换算值及其改正数

1 张正禄、李广云、潘国荣等.工程测量学[M].武汉：武汉大学出版社，2005：31～35

2 杨德麟.大比例尺测图的原理方法与应用[M].北京：清华大学出版社，2002：133～143

3 潘正风.数字测图原理与方法[M].武汉：武汉大学出版社，2004：150～152

4 金国兴、刘大杰、施一民.GPS定位的应用与数据处理[M].上海：同济大学出版社，1994：120～125

5 桑吉章.GPS定位结果的坐标转换[J].城市勘测，1999(3)：10～13

6 周家香、左廷英、朱建军.地理数据的几何校正方法[J].矿山测量，2004(4)：25～27

7 王建弟.用二次多项式实现54坐标到80坐标的转换[J].矿山测量，2005(3)：29～32

8 刘云峰、李 若.数字地图产品生产坐标系统转换问题的探讨[J].测绘技术装备，2004(2)：20～23

9 李志林、朱 庆.数字高程模型[M].武汉：武汉测绘科技大学出版社，2000：165～166

10 於宗寿、鲁林成.测量平差原理[M].北京：测绘出版社，1994：55～60

Implementing of coordinate transfering between two survey system in engineering survey

Zhao Xiaoling

Coordinate error is produced by taking deterministic transformation parameters in ordinary coordinate transformation mode1.Regarding common point in diferent coordinate system as discrete point, w ith same accuracy in conversion zone, approximate conversion coordinates and it’s corrective values of common points are obtained by calculating barycentric coordinates and initial conversion parameters.According to the coresponding relation between old coordinates and corective values of common points, corective values of unknown conversion cordinates are obtained by using interpolating function in ordinary digital mapping software, and coordinates in different system are conversed. Application indicates that this method, w ith a simple model and a high conversion accuracy, is a efective way of coordinate transformation.

engineering survey; coordinate transformation; initial conversion parameters; coordinate corective value

TB22

A

1000－8136(2010)12－0038－02