解特殊凸二次半定规划的边界点法
2010-01-15李成进
李成进
(福建师范大学 数学与计算机科学学院,福建 福州 350007)
1 前言
本文将要考虑的是具有如下形式的凸二次半定规划问题:

其中,实数a≠0,b∈Rm,C∈Sn,符号<.,.>表示Frobenius内积,而Rm,Sn,分别表示m-维实向量空间,n×n实对称矩阵空间表示空间以及Sn中的半正定矩阵锥。另外,I表示单位矩阵,线性算子φ(X):=(<A1,X>,Λ<Am,X>),其中
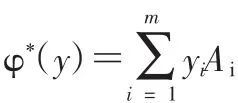
问题(1.1)是特殊的非线性半定规划问题,因此可以利用文献[1]中的过滤集序列线性化方法来求解。但考虑到其特殊结构,故而本文将利用边界点法对其进行求解。
易知,问题(1.1)的KKT条件为:

它又等价与以下的条件:

A:=(svec(A1),svec(A2),svec(Am))T
则可以得到φ(X)=Asvec(X),φ*(y)=smat(ATy)为了讨论方便,假设以下的假定条件成立。
假定1.1 矩阵A满行秩;且问题(1.1)存在严格可行点,即Slater条件成立。
最后,介绍一下本文的结构:在第二节中将介绍解问题(1.1)的边界点法,同时分析其全局收敛性;而在第三、四节中分别给出其初步的数值试验与结论。
2 边界点法
通过条件(1.3)可以很容易地构造出解问题(1.1)的边界点法:由初始点S0出发,在第k-次迭代中先暂时固定S=Sk然后通过(1.3)的第三式求出yk+1;当yk+1确定下来后可由(1.3)中的第一、二式再求出Xk+1与Sk+1。把上述过程编成程序便可得到以下的边界点法。
算法2.1(边界点法)
取ε>0,k=0,Sk=0,δ≥ε;
重复迭代直至δ<ε被满足。
求解yk+1:AATyk+1=ab-Asvec(Sk-C);

δ=‖φ(Xk+1)-b‖/(1+‖b‖2);
k=k+1;
结束。
其中‖·‖F,‖·‖2分别表示矩阵空间的F-范数与向量空间的2-范数。算法2.1的运行过程中不需要用到文献[2]中边界点方法的外部迭代,这是因为(1.2)的第一个等式中包含X。
由构造可知,每次由边界点法产生的迭代点对X,S满足

这就是“边界点”这个名称的由来。停止准则‖φ(X)-b‖≤ε保证迭代点列的极限点会充分接近问题(1.1)的可行域。
定义y(S):=(AAT)-1(b-Asvec(S-C)),V(S):=smat(AT(y(S)))-C=smat[AT(AAT)-1b-AT(AAT)-1Asvec(S-C)]-C,P(V):=(V1,V2):=(a-1(V);(-V))
以及M:=AT(AAT)-1A,接下来先介绍文献中的一个重要结论。
引理2.2 对任意的V,V∈Sn有

类似于文献[3]中引理2.7的证明过程,可推导下引理。
引理2.3 对任意的S,S∈有

证明:直接计算可得V(S)-V()=smat(Msvec(-S))而M是一个谱半径为1的正交投影矩阵,从而有
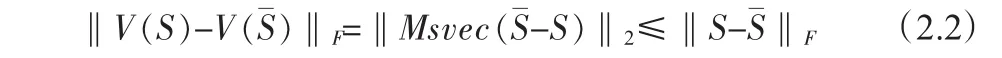
上述引理说明算子P(V(·))是收缩的,这对于边界点法的全局收敛性分析是至关重要的。
引理2.4 设(X*,y*,S*)其中y*=y(S*)是问题(1.2)的一个解并且X,S∈,XS=0。如果
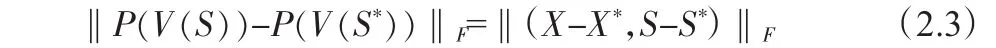
那么(X,S)是个不动点,即,(X,S)=P(V(S))因此,(X,y,S),其中y=y(S),是问题(1.1)的一个KKT点。
证明:由引理2.2与引理2.3可知
‖P(V(S))-P(V(S*))‖F≤‖V(S)-V(S)*‖F≤‖S-S*‖F联立(2.3)与‖S-S*‖F≤‖X-X*,S-S*‖F,可得
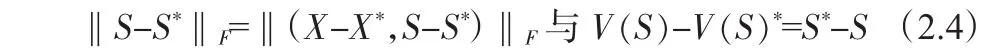
成立。从而有

再由(1.2)的第一个等式,V(S)*的公式,(2.5)以及(2.4)的后一式,可推导出

联立(2.6)式与X,S∈,XS=0可得到(X,S)=PV(S)证毕。
现在,可以来推导本节的主要结论了。
定理2.5 从任意一个起始点(X0,y0,S0)开始迭代,由算法2.1产生的迭代点列(Xk,yk,Sk)收敛到点(X*,y*,S*)∈Θ其中Θ表示(1.2)的解集。
证明:对任意的(X*,y*,S*)∈Θ由P(V(·))的收缩性可得
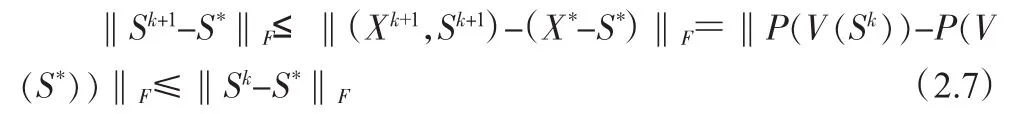
从而有{Sk}是一个紧集.由(2.7)的后三个关系式与集合{Sk}的紧性可推导出点列{(Xk,Sk)}是一紧集,故而至少存在一个聚点,不妨设其中{kj}是指标集{k}的某个子集。由算法2.1中对Xk,Sk的迭代更新可知,且<,>=0。
联立(2.7)的后三个关系式与‖Sk-S*‖F≤‖(Xk-Sk)-(X*-S*)‖F,可得序列{‖(Xk,Sk)-(X*,S*)‖F}是单调下降的。因此,

其中(X′,S′)可以取为点列{(Xk,Sk)}的任意一个聚点。由P(V(·))的连续性可知的像

也是{(Xk,Sk)}的一个聚点。因此有
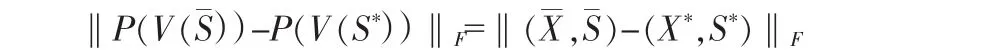
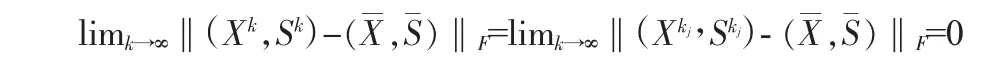
即,点列(Xk,Sk)收敛到唯一的一个极限点(,)证毕。
3 结论
本文给出了解一类特殊凸二次半定规划问题的边界点算法,并证明了其具有全局收敛性。最后,还针对此算法进行了初步的数值试验,得到的数据证实了边界点法的有效性。
[1]C.J.Li and W.Y.Sun,On filter-successive linearization methods for nonlinear semidefinite programming[J].Sci,2009,(39).
[2]J Povh,F Rendl,A Wiegele.A boundary point method to solve semidefinite programs[J].Computing,2006(78).
[3]Z Wen,D Goldfarb,W Yin.Alternating direction augmented lagrangian methods for semidefinite programming[J].preprint,2009,(10).
