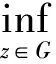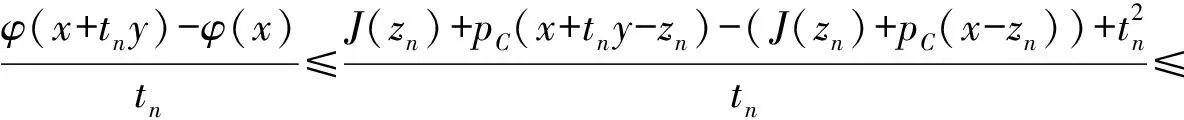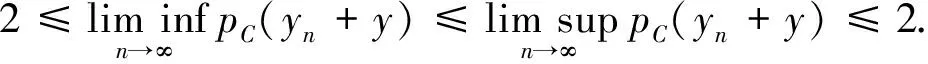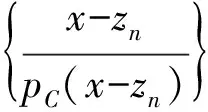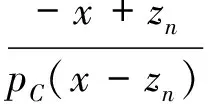Banach空间中一类广义扰动优化问题最优解的存在性*
2010-01-11何金苏
何金苏
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
0 引 言
设X是维数至少为2的实Banach空间,X*表示X的共轭,A为X的非空闭子集,intA,∂A分别表示有界集A的内部和边界,B(x,r)表示X的以x为中心r为半径的闭球,特别令B=B(0,1).
设C是X的闭有界凸子集,且0∈intC,显然C是X的吸收集但不一定对称.定义
pC(x)=inf{α>0:x∈αC},∀x∈X.
称pC(x)为集合C上的Minkowski泛函.
设G是X的非空闭子集,J:G→R是下半连续下有界函数.对∀x∈X,考虑广义扰动优化问题
(1)
显然,当C=B时,pC(5)是范数‖5‖,(JC,x)-inf问题即为文献[1]中的扰动优化问题.扰动优化问题最先由Baranger在文献[2]中提出,由于该类扰动优化问题在由偏微分方程决定的优化控制问题中有着广泛的应用[2-4],因此引起了很多优化和逼近论学者的重视[5-7],但对广义扰动优化问题的研究未见报道.本文主要借助集合的紧性概念和广义最优值函数的方向导数,研究广义最优解的存在性,推广了文献[1,8]中的部分结果.
1 预备知识
首先给出Minkowski泛函的一些已有性质,具体可参阅文献[8-10].
命题1设C如上定义,则对于任意x,y∈X,有
1)-pC(y-x)≤pC(x)-pC(y)≤pC(x-y);
2)(pC(x+ty)-pC(x))/t≤(pC(x+t′y)-pC(x))/t′,∀t,t′∈R{0},t -pC(y-x)≤dG(x)-dG(y)≤pC(x-y),且|dG(x)-dG(y)|≤υ‖x-y‖. 定义1令y∈∂C. 2)对任意y∈∂C,C在y处紧局一致凸,则称C紧局一致凸. 定义2设{zn}⊆G,若 则称{zn}为x的JC-极小化序列. 定义3设x∈X,若x的任何JC-极小化序列{zn}均有收敛于G中元的子列,则称G在x处是JC-逼近紧;若对任意x∈X,G在x处JC-逼近紧,则称G是JC-逼近紧. 设G是Banach空间X的非空闭子集,C是X的闭有界凸子集,且0∈intC.定义X上的函数φ为 (2) 则由命题2可知φ是Lipschitz连续,即 |φ(x)-φ(y)|≤υ‖x-y‖,∀x,y∈X. (3) 对x,y∈X,用φ′+(x)(y)表示φ在x处沿y方向的方向导数,其定义为 (4) 接下来主要讨论广义最优值函数φ(x)的方向导数之值同相关集G的JC-逼近紧性和问题(JC,x)-inf最优解存在性的关系. 引理1设x∈XG,y∈∂C,使 (5) (6) 不妨设tn 因此 定理1设x∈XG,y∈∂C,使式(5)成立.若C在y处紧局一致凸,则G在x处是JC-逼近紧的. 证明 设{zn}⊂G是x的任一JC-极小化序列,则由引理1有 不失一般性(取子列),可设 由定理1可得: 推论1设C是紧局一致凸空间,若对于任意x∈XG,存在y∈∂C,使φ′+(x)(y)=1,则G是JC-逼近紧集.因而,对任意x∈X,问题(JC,x)-inf的最优解存在. 注1当pC(5)是范数(C=B)时,定理1即为文献[1]中的定理4.1;当J(x)=0时,定理1即为文献[8]中的定理3.1. 定理2若x∈XG,y∈∂C,使 (7) 若C在y处紧局一致凸,则对任意x∈X,问题(JC,x)-inf的最优解存在. 证明 由式(7)可取{tn},使tn→0+,且 取zn∈G,满足0 J(zn)+pC(x+tny-zn)<φ(x+tny)+tn2. 事实上,因为 φ(x)≤J(zn)+pC(x-zn)≤J(zn)+pC(x-zn+tny)+pC(tny)=J(zn)+pC(x-zn+tny)+tn≤ φ(x+tny)+tn+t2n≤φ(x)+2tn+t2n, 所以令tn→0+,得 (8) 则{zn}是x的一个JC-极小化序列.进一步,不妨设 由命题1的2)知 (9) 所以,z0是问题(JC,x)-inf的最优解.定理2证毕. 推论2设X紧局一致凸,G是X的非空闭子集.若对于任意x∈XG,存在y∈∂C,使φ′+(x)(y)=-1,则对任意x∈X,问题(JC,x)-inf的最优解存在. 注2当J(x)=0时,定理2即为文献[1]中的定理4.2. [1]何金苏.Banach空间中一类扰动优化问题最优解的特征与存在性[J].数学学报,2007,50(3):669-678. [2]Baranger J,Temam R.Nonconvex optimization problems depending on a parameter[J].SIAM J Control,1975,13(1):146-152. [3]Bidaut M F.Existence the theorems for usual and approximate solutions of optimal control problem[J].J Optim Theory Appl,1975,15(4):393-411. [4]Cobzas S.Nonconvex optimization problems on weakly compact subsets of Banach spaces[J].Anal Numer Theor Approx,1980,9(1):19-25. [5]Ni Renxing.Generic solutions for some perturbed optimization problem in non-reflexive Banach space[J].J Math Anal Appl,2005,302(2):417-424. [6]Baranger J.Existence de solution pour des problemes d′ optimization nonconvex[J].C R Acad Sci Paris,1972,274:307-309. [7]Cobzas S.Generic existence of solutions for some perturbed optimization problems[J].J Math Anal Appl,2000,234(2):344-356. [8]Li Chong,Ni Renxing.Derivatives of generalized distance functions and existence of generalized nearest points[J].J Approx Theory,2002,115(1):44-55. [9]De Blasi F S,Myjak J.On a generalized best approximation problem[J].J Approx Theory,1998,94(1):54-72. [10]Li Chong.On well posed generalized best approximation problem[J].J Approx Theory,2000,107(1):96-108.

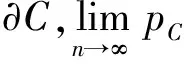

2 主要结果