有时间窗物流配送路径优化问题的混合并购算法＊

赵建民, 刘芳华, 徐慧英, 朱信忠

(浙江师范大学数理与信息工程学院,浙江金华 321004)

0 引 言

随着市场经济的发展,物流配送在货物运输成本中所占的比例越来越高.物流配送路径优化问题就是通过合理配送路线,使总运行距离最短或总成本最低.有时间窗物流配送路径优化问题则是在物流配送路径优化问题的基础上,增加了有时间窗约束的条件.解决有时间窗物流配送路径优化问题的常用算法有:遗传算法[1-4]、禁忌搜索算法、蚁群算法[5]等.目前,在 Solomon Benchmark problems数据集上实验获得最佳效果的方法分别为:进化启发式算法[6]、概率多元化算法[7]、禁忌算法[8]、混合算法[9]和节约法[10].

并购算法是通过并购、重组操作达到资源整合、优化配置的企业并购行为,是基于企业并购思想之上形成的一种优化方法.企业并购是在市场经济环境下,根据市场自身规律,企业在诞生、发展、灭亡的过程中形成的市场资源的再整合,也是优化市场资源配置的市场自身调节行为.根据并购操作的不同,又分为单一并购算法 (也简称并购算法,http://www.idsia.ch/～luca/macs-vrptw/problems/welcome.htm)和混合并购算法.本文通过建立混合并购算法模型,把混合并购算法应用到有时间窗物流配送路径优化问题中,获取有时间窗物流配送路径问题的最优解或近似最优解.

1 物流配送路径优化问题的数学模型

1.1 符号定义

有时间窗物流配送路径优化问题模型涉及到客户数量、客户需求量、汽车数量、汽车载重以及时间窗等,为了操作方面,特定义变量如下:

n:客户数量;dij:客户点 i到客户点 j的距离;K:汽车的总数;qk(k=1,2,…,K):车辆 k的最大载重量;gi(i=1,2,…,n):客户点 i的货物需求量;wd:单位距离成本惩罚权重;wq:超出最大载重量的单位载量成本惩罚权重;we:客户点的单位等待时间惩罚权重;wl:客户点的单位迟到时间惩罚权重;ti:到达客户 i的时间;[ETi,LTi]:客户点 i要求的时间窗,其中 ETi是客户要求被服务的时间窗的始点,LTi是客户要求被服务的时间窗的终点.

1.2 目标函数及约束条件

有时间窗物流配送路径问题的目标就是获取问题的最优解或近似最优解,即使物流配送的成本最小化.但要达到所求的目标,就要满足相关约束条件.定义变量如下:

目标函数

式 (1)中:minZ表示完成物流配送的最小运行成

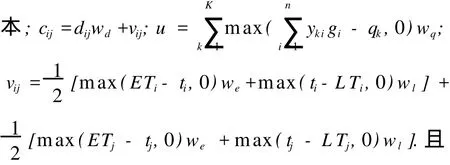
满足以下约束条件:

其中:式 (2)表示某车辆所访问的客户需求量之和不能超过车辆的最大载量;式 (3)表示客户点 i由车辆 k完成的唯一性;式 (4)和式 (5)表示到达客户的车辆的唯一性.

2 混合并购算法在有时间窗物流配送路径优化问题中的应用

2.1 混合并购算法简介

混合并购算法是在并购算法的基础上形成的,也是基于企业并购思想之上形成的一种优化方法.混合并购算法包括企业生态编码、初始化企业生态、预处理企业生态、评估劣信度、混合并购操作、重组操作、选择操作主要行为,其流程图如图 1所示.

混合并购算法的主要步骤如下:

步骤 1 参数设置及初始化.企业生态链条数 NT;循环迭代次数 Nc=1;最大迭代次数 Nmax;当前参与出售的企业集团标识 Group M ark=ones(NT,1);当前参与出售企业个体标识Single M ark=ones(NT,1);MASingleSum是 som e函数获取的企业个体总数;GroupChain表示NT个企业生态链;GroupSum为当前企业链上企业集团的数目;随机生成 NT条企业生态链,每条链上有 n个企业个体;当前企业生态所执行的并购操作类型 runType=zeros(NT,1),zeros是赋值为 0的函数.

图 1 混合并购算法流程图

步骤 2 预处理操作.针对具体求解的问题,降解约束条件,对企业生态进行预处理操作.

步骤 3 若 Nc≤Nmax,判断迭代次数是否达到最大迭代次数,如果是,就结束循环,转至步骤8;否则,继续循环,转至步骤 4.

步骤 4 混合并购操作.令 SingleChain =GroupChain(i).则

若 runType(i)=0,则执行单个并购操作:先修正参数 Group M ark(i),Single M ark(i),再对企业生态链进行单个并购操作,即把 Single M ark(i)分别预出售给其他企业集团,计算 min{cost(1),cost(2),…,cost(GroupSum(i))},选择劣信度最小的企业集团 k作为并购的主体.

若 runType(i)=1,则执行多个并购操作:依次选取临时企业个体集合 T=Tem p,把 Tem p预出售给其他企业集团,计算min{cost(1),cost(2),…,cost(GroupSum(i))},选择劣信度最小的企业集团 E,最后确认把 Tem p出售给企业集团 E.

步骤5 重组操作.令 S ingleChain =GroupChain(i).则

1)插入法部分:待重组企业个体集合 T=som e(S ingleChain(j)),把 T中的每一个企业个体先后插入至当前企业集团 j内部适当位置,计算min(cost(S ingleChain(j))),保证当前企业集团 j的劣信度最小.

2)调整法部分:依次取出企业集团 j中的每一企业个体,插入至当前企业集团 j内部适当位置,计算 min(cost(S ingleChain(j))),保证当前企业集团 j的劣信度最小.

步骤 6 劣信度评估.根据并购算法中的劣信度评估及求解的具体问题,分别定义 3个劣信度的计算方法或影响劣信度的要素.用 cost函数计算劣信度.

步骤 7 选择操作.若 runType(i)=0,则执行以下操作:根据得到的新企业生态链劣信度,如果低于旧的企业生态链劣信度,则更新企业生态链,修正参数 Group M ark(i),runType(i);否则,不更新,修正 S ingle M ark(i),并记录符合要求的最佳企业生态链.

若 runType(i)=1,则执行以下操作:根据得到的新企业生态链劣信度,如果低于旧的企业生态链劣信度,则更新企业生态链,修正参数runType(i),Group M ark(i),S ingle M ark(i),并记录符合要求的最佳企业生态链;否则,只更新当前企业生态链,继续下一次循环,转至步骤 3.

步骤 8 程序结束,获得最佳企业生态链.

注 1 一般地,将 som e函数定义为:取出企业集团内部的一部分企业个体.企业个体的选择原则是:计算 max{cost(1),cost(2),…,cost(x)},选择企业个体劣信度最大的客户个体 p及其左侧(或右侧)的所有企业个体,具体数目以不大于当前企业集团内企业个体总数的 1/2为准则.

2.2 有时间窗物流配送路径优化问题应用模型

根据混合并购算法的思想,结合对有时间窗物流配送路径优化问题的研究,把混合并购算法应用到有时间窗物流配送路径优化问题中,建立对应的问题模型,即企业生态编码、初始化企业生态、预处理企业生态、评估劣信度、混合并购操作、重组操作、选择操作等.

1)企业生态编码.采用自然数直接编码的方法,把一个企业的个体对应至物流配送中的一个客户.设共有 n个客户,用 0表示配送中心,用1～n的自然数分别对 n个客户编号,根据可供使用的汽车总数 K,分成 K组,所形成的编码就代表一个企业生态链,多条企业生态链就构成了企业生态 (市场).

2)初始化企业生态.根据企业生态链编码方法,产生一条企业生态链,M条这样的企业生态链就构成了企业生态.

3)预处理企业生态.在初始化的同时,用不考虑时间窗和最大载重等因素、只考虑距离因素的并购算法处理物流配送路径优化问题,可以迅速获得初始化的最优解,有利于提高混合并购算法的效率.

4)评估劣信度.要判断某条企业生态链所对应的配送路径方案的优劣,完全由劣信度决定.所谓劣信度,就是企业个体、企业集团或企业生态链上运行成本高低的判断标准,劣信度越低,运行成本越低,否则运行成本越高.根据不同的对象,劣信度计算标准也不一样;根据并购操作的选择不同,劣信度评估的标准也有可能不同.只有在定义企业个体劣信度评估时,才会根据单个或多个并购操作,分别定义企业个体劣信度.

企业个体劣信度评估只局限于某个企业集团中.在物流配送路径优化问题中,它的劣信度包括3个部分,分别是在任一个车辆配送路径方案中,当前配送客户与其他客户间的运输距离成本 cs,完成当前客户配送的等待时间成本 ce,完成当前客户配送的迟到时间成本 cl.这 3个部分的成本之和就构成了企业个体的劣信度.根据并购操作的不同,对距离成本的定义有所不同.如果是单个并购操作,距离成本则定义为:在车辆配送路径方案中,当前客户偏离其他客户的距离成本;如果是多个并购操作,距离成本则定义为:在车辆配送路径方案中,当前客户偏离其他客户的距离成本,以及偏离与之相邻客户的距离成本.则企业个体的劣信度评估函数为 cs+ce+cl.

企业集团劣信度评估,就是对企业集团内部生态链进行劣信度评估.在物流配送路径优化中,它的劣信度包括 4个部分,即是在任一个车辆配送路径方案中,完成客户配送所需的运输距离成本 cs,运输超载成本 cq,完成所有客户配送的等待时间成本之和 ce,完成所有客户配送的迟到时间成本之和 cl.企业集团的劣信度评估函数为 (cs+ce+cl)exp(cq).

企业生态链劣信度评估,则只针对一个生态链而已.在物流配送路径优化问题中,它的劣信度也包括 4个部分,分别是在物流配送方案中,完成所有客户配送所需的运输距离成本 Cs,运输超载成本之和 Cq,完成所有客户配送的等待时间成本之和 Ce,完成所有客户配送的迟到时间成本之和cl.则企业生态链的劣信度评估函数为 (Cs+Ce+Cl)exp(Cq),也即是一个完整的物流运输配送方案的运行成本 (式 (1)).

5)混合并购操作.混合并购操作只针对每一条企业生态链上的企业集团和个体.如果是单个并购操作,则遵循以企业集团劣信度从高到低、企业个体劣信度从高到低的原则,逐步出售.收购的企业集团则是按从低到高的原则去收购出售的企业个体.如果是多个并购操作,则由所有企业集团的某些企业个体组成出售的个体集合,分别出售给企业集团劣信度变化最小的企业集团.

6)重组操作.采用插入法和调整法相结合的方法.但插入法在运用上与单一并购算法中的重组操作略有不同.插入法操作的对象不再是集团内部所有个体,而是随机抽取集团内部相邻的部分个体 (不大于内部个体总数的 1/2)集合.每次操作随机选择一个对象,以插入后当前企业集团劣信度最低为准则,选择判断插入位置.由于后插入的每一个客户都可能对其他客户产生影响,为了降低影响,需对其再进行调整.所谓调整法,就是对链上每个客户所在的位置按以下规则进行调整:如果该位置上客户的当前企业集团劣信度不是最低的,则将其调整至最佳位置.当然,调整的次数越多,重组效果越好,但重组效率随之降低,本文只做一次调整.

7)选择操作.无论是单个并购操作还是多个并购操作,在每次并购、重组之后,判断每一条企业生态链劣信度是否降低.如果降低,则更新企业生态链,否则,不更新.如果当前操作是单个并购操作,且操作还没有达到终止条件,算法不能再收敛,单个并购算法就有可能“陷入局部最优”,因此可把单个并购操作修改为多个并购操作,继续循环;如果当前操作是多个并购操作,在每次并购、重组之后,判断每一条企业生态链劣信度是否降低.如果降低,则把多个并购操作修改为单个并购操作,否则,不更新并继续循环.同时,在当前企业生态中,记录劣信度最低的企业生态链,暂时作为当前最佳物流配送方案.

3 实验与数据分析

基于MATLAB 7.0开发平台,编程实现了有时间窗物流配送路径优化问题的混合并购算法,进行了算法原型系统的构建和模拟运行,并进行了数据的实验和分析.实验采用 Solomon所设计的 Solomon Benchmark problems数据集 (http://www.idsia.ch/～luca/macs-vrptw/problems/welcome.htm).其中,每一个问题类型都有 100个客户,共有 C1,C2,R1,R2,RC1,RC2等 6大类的 56种问题类型.

实验参数说明:(RT,EC,wq,wd,we,wl)=(迭代次数,企业生态链数目,单位超载载量成本惩罚权重,单位距离成本惩罚权重,等待时间惩罚权重,迟到时间惩罚权重).硬件环境:CPU:Genuine Intel 1.86 GHz;内存 :1 G;运行时间 :600 s以内为宜.最后把实验结果与目前已知的最优解[11]进行比较,结果如表 1所示.其中:Data代表问题类型;K代表需求的汽车数;TD代表汽车总的行驶路程;ET代表等待时间;LE代表迟到时间;N表示第一目标与已知最优解的相对误差;T表示第二目标与已知最优解的相对误差.其中,Data,K是设置变量,TD,ET,LE是通过获取最小成本最优解 (式 (1))对应的物流配送方案得出的.

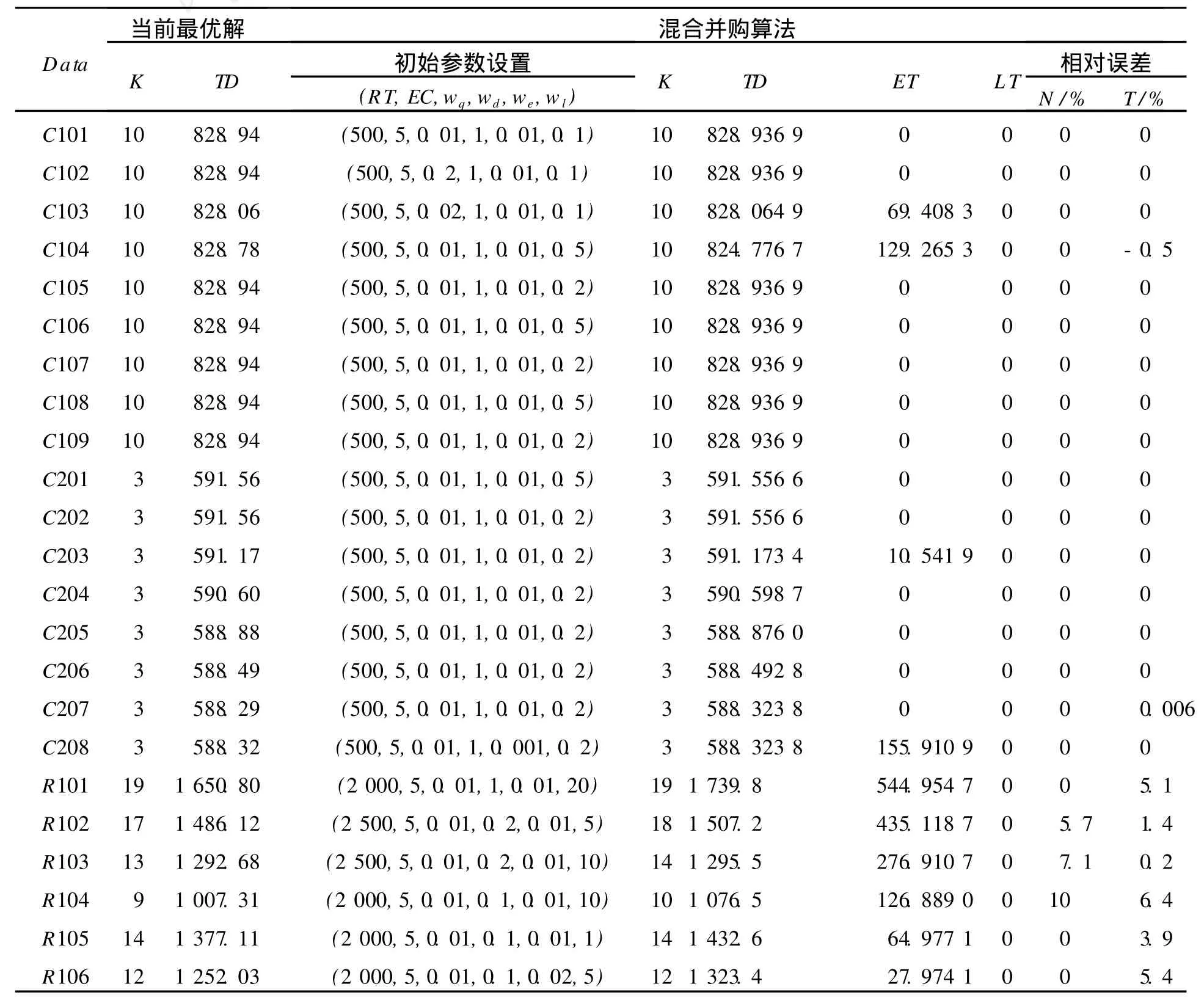
表 1 混合并购算法在 Solomon数据集上的实验结果

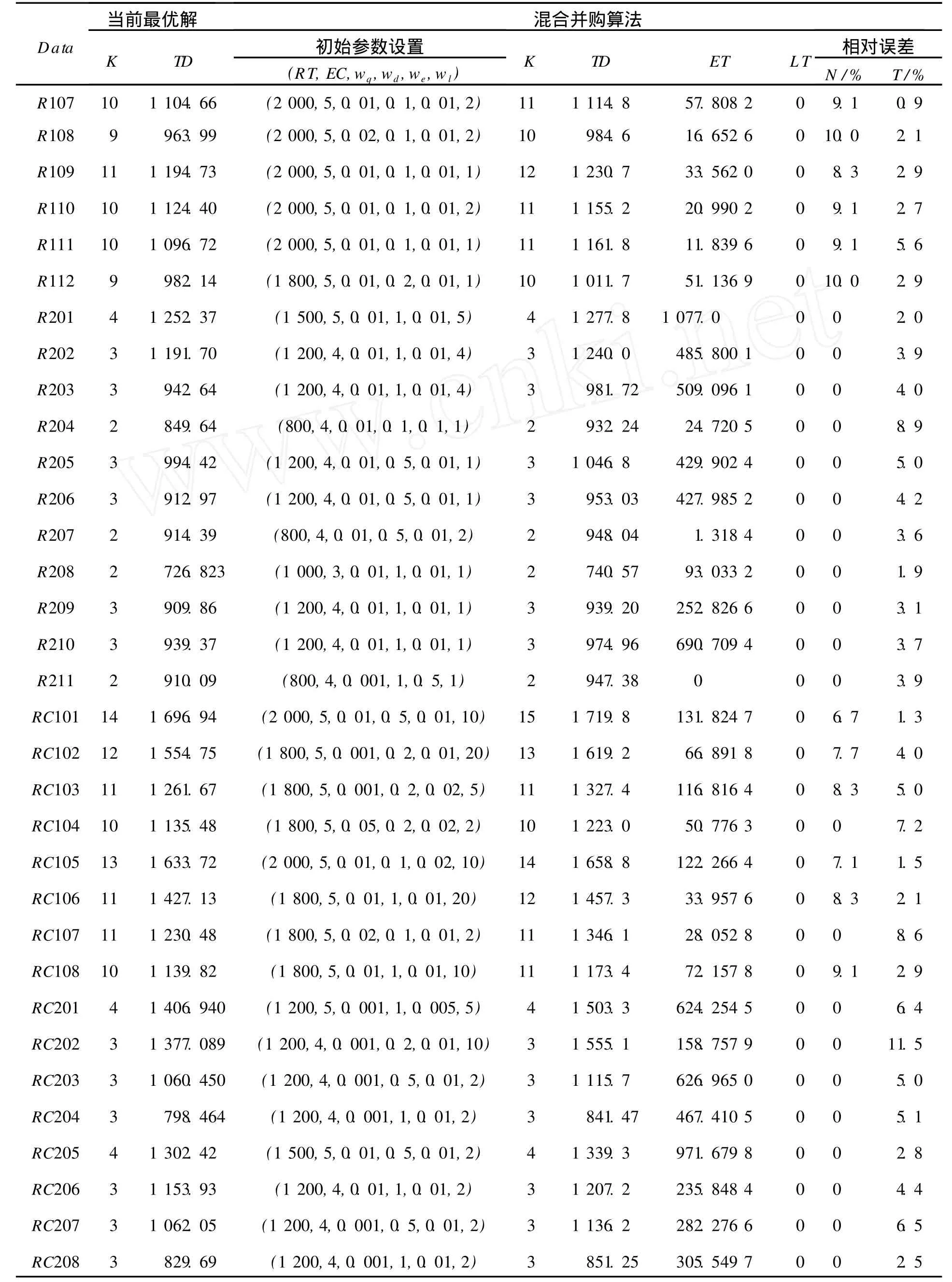
续表1

通过对实验数据分析得出:1)混合并购算法在解决 C类问题上效果最为明显,第一目标和第二目标都达到了最优解,比近似算法[12]的最优解还要好,而且在 C104类问题上获得了更优解;2)混合并购算法在求解 R2和 RC2类问题上效果也比较好,第一目标达到了最优解,第二目标也基本接近最优解,与近似算法获得的最优解差不多;3)混合并购算法在解决 R1和 RC1类问题上效果不甚理想,虽然部分问题类型在第一目标上也达到了最优解,但与近似算法的最优解或目前最优解相比,都还有进一步改进的空间.原因是这两种问题类型的客户点分布分散,客户之间的相互影响不大,且时间窗宽窄不一,增大了求解难度.

通过对算法模型分析得出:1)混合并购算法是在并购算法的基础上形成和发展的,能有效地解决单一并购算法“陷入局部最优”的不足;2)混

合并购算法的时间复杂度不高于其他传统算法的时间复杂度,如遗传算法、蚁群算法;3)混合并购算法在求解有时间窗物流配送路径优化问题时,大部分问题类型获得了最优解或近似最优解;4)混合并购算法是一种求解物流配送路径优化问题的新算法,拓宽了求解问题的渠道和方法.

4 结 语

混合并购算法是在单一并购算法的基础上改进而成的,不仅继承了单一并购算法的优点,而且有效地解决了单一并购算法“陷入局部最优”的不足.通过模拟实验,获得了有时间窗物流配送路径优化问题的最优解或近似最优解,体现混合并购算法的可行性、有效性、收敛性.虽然在 Solomon数据集上得到了很好的效果,但仍有进一步改进的空间.

[1]BakerB M,Ayechew M A.Agenetic algorithm for the vehicle routing problem[J].Computers&Operations Research,2003,30(5):787-800.

[2]Hanshar F T,Ombuki-Ber man B M.Dynamic vehicle routing using genetic algorithms[J].Applied Intelligence,2007,27(1):89-99.

[3]Alvarenga GB,Mateus G R,de Tomi G.A genetic and set partitioning two-phase approach for the vehicle routing problem with time windows[J].Computers&Operations Research,2007,34(6):1561-1584.

[4]Beatrice O,Brian J R,Franklin H.Multi-objective genetic algorithms for vehicle routing problem with time windows[J].Applied Intelligence,2006,24(1):17-30.

[5]Chen Chiaho,Ting Chingjung,Chang Peiahan.Applying a hybrid ant colony system to the vehicle routing problem with time windows[J].Journal of the Eastern Asia Society of Transportation Studies,2005(6):2822-2836.

[6]Homberger J,Gehring H.Two evolutionary metaheuristics for the vehicle routing problem with time windows[J].I NFOR,1999,37(3):297-318.

[7]Rochat Y,Taillard E.Probabilistic diversification and intensification in local search for vehicle routing[J].Journal of Heuristics,1995,1(1):147-167.

[8]Taillard E,Badeau P,GenderauM,et al.A tabu search heuristic for the vehicle routing problem with soft time windows[J].Transportation Science,1997,31(2):170-186.

[9]Thangiah S R,Osman IH,Inayagamoorthy R,et al.Algorithms for the vehicle routing problemswith time deadlines[J].Amer J MathManagement Sci,1994,13(3/4):323-355.

[10]刘芳华,赵建民,徐慧英.基于并购算法的物流配送路径优化的研究[J].计算机与数字工程,2009,37(8):25-28.

[11]Bent R,Van Hentenryck P.A Two-Stage Hybrid Local Search for the Vehicle Routing Problem with Time W indows[J].Transportation Science,2004,38(4):515-530.

[12]刘小兰,郝志峰,汪国强,等.有时间窗的车辆路径问题的近似算法研究[J].计算机集成制造系统,2004,10(7):825-831.