区间数判断矩阵的满意一致性及排序方法

王西静

(晋城职业技术学院数学系,山西晋城 048026)

0 引 言

利用区间数判断矩阵的一致性和排序方法是区间数层次分析法的2个重要的课题.一些学者依据权重可行域建立线性规划模型,用模型的极点来表示区间数判断矩阵的权重范围,显然此方法只适用于满足一致性的区间数判断矩阵[1-3].Saaty等[4]提出了Monte Carlo模拟方法确定区间数判断矩阵的排序权值.Wang等[5]给出了对一致性和不一致性区间数判断矩阵均适用的区间数判断矩阵排序权值的方法.冯向前等[6]指出现有的满意一致性定义大多是通过判断在决策允许偏差下是否具有一致性来衡量判断矩阵是否是满意的.但是,如果偏差设得较小,可能使得扩大后的区间数判断矩阵不具有一致性信息,而偏差设得较大又会使原有区间数判断矩阵表达的优先信息变得更加模糊,此时产生的排序权值是否合理则是一个值得讨论的问题[7].Wang等[8]提出一种不改变区间数判断矩阵的元素,在区间数判断矩阵中求具有满意一致性的排序权值的思路,但是并没有给出满意一致判别方法.基于此,本文从理论上对此进一步做了补充,给出了区间数判断矩阵的满意一致性的判别方法,并且证明了此方法适用判别区间数判断矩阵是否具有一致性.另外,还给出了求解排序向量的优化模型,并用算例证明不论区间数判断矩阵是否具有一致性,此模型均适用.

1 区间数判断矩阵的满意一致性

定义1 称A=(aij)n×n是区间数判断矩阵,如果对任意的i,j∈N={1,2,…,n}均有:aij=[lij, uij],且0＜ lj≤uij;aij=1/aji,aii=1.

定义2[7]称区间数判断矩阵 A=(aij)n×n具有一致性,若存在数字判断矩阵A—= (a—ij)n×n,a—ij∈[lij,uij],具有一致性.

定义3 称区间数判断矩阵A=(aij)n×n具有满意一致性,若存在数字判断矩阵A—= (a—ij)n×n,a—ij∈[lij,uij],具有满意一致性.

引理1[9]设A—=(a—ij)n×n是数字判断矩阵,则对任意标准化数字向量w—=(w—1,w—2,…,w—n)T,有,

定理1[9]设A=(aij)n×n为区间数判断矩阵, A具有满意一致性的充分必要条件是集合Tw—非空,其中,

其中,w—=(w—1,w—2,…,w—n)T,δ是满意一致性指标,一般取δ≤0.1,RI为平均随机一致性指标[1].

对于区间数判断矩阵 A(aij)n×n,要检验其是否具有满意一致性,由定理1知,需要判断集合 Tw—是否非空.为此,特建立下面的非线性规划模型 P1.

定理2 设 A=(aij)n×n为区间数判断矩阵, δ＊是模型 P1目标函数的最优值,则:A具有一致性的充要条件是,δ＊=0;A具有满意一致性的充要条件是,δ＊≤δU,其中,δU是满意一致性指标阙值.

证明 根据定理1,易证定理2之②成立,下面证明定理2之 ①成立.

若δ＊=0,则存在a—ij、w—i≥0,i,j∈N,使得,

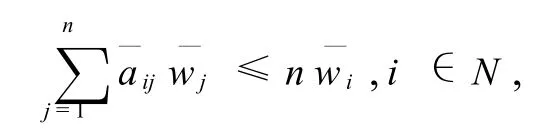
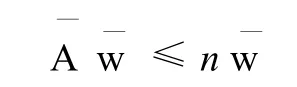
根据引理1知,Aw—≥nw—,所以,A—w—=nw—,由引理2知,对于区间数判断矩阵A,存在数字判断矩阵A—(—aij∈aij)具有一致性,故 A具有一致性.

若 A具有一致性,则存在数字判断矩阵A—= (a—ij)n×n,a—ij∈aij,具有一致性,即存在标准化向量w—=(w—1,w—2,L,w—n)T,使得,

即,

所以,δ＊≤0,根据引理1知,δ＊≥0,因此,δ＊=0.

定理证毕.

综上所述,定理2说明了模型 P1不仅可以用来判别区间数判断矩阵是否具有满意一致性,同时还可以用来判别区间数判断矩阵是否具有一致性.

2 排序方法

对具有满意一致性的区间数判断矩阵A,可以采用下面的规划模型 P2来求解判断矩阵的区间数排序向量.

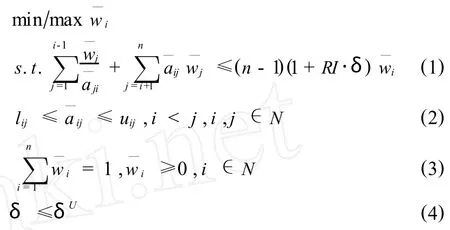
下面证明,若令δU=0,则模型 P2等价于文献[8]给出的线性规划模型 P3,

事实上,我们只需证明,当δ=0时,式(1)、(2)等价于式(5).若存在w—i≥0,i∈N,使得式(1)成立,则有,A—w—≤n w—.根据引理1可得,A—w—= n w—,又根据引理2有,a—ij=w—i/w—j,i,j∈N,代入式(2)直接得到式(5).反之,若存在w—i≥0,i∈N使得式(5)成立,令a—ij=w—i/w—j,i,j∈N,则A—= (aij)n×n具有一致性,根据判断矩阵的互反性易得式(1)成立.

由此可知,模型 P2既适用于求解不一致的区间数判断矩阵的排序向量,也适用于求解一致的区间数判断矩阵的排序向量.

3 算例分析

通常,供应链伙伴企业之间的合作状况,直接关系到供应链系统运作的绩效与成败.因此,企业在选择合作伙伴时,常需要对伙伴企业的绩效、业务能力、质量管理系统以及企业所处的环境进行综合评价[10].假设某企业拟在4个企业{X1,X2,X3,X4}中选择合作伙伴,并聘请了 m个专家进行决策(m≥2),专家根据企业的基本状况进行两两比较,给出如下的区间数判断矩阵B,

对此,我们可首先考查判断矩阵的合理性,即把判断矩阵B的数据代入规划模型P1,求解得,δ＊= 0.0168＜0.1,说明判断矩阵具有满意一致性.进一步,取δU=0.1,求得区间数排序向量w为,

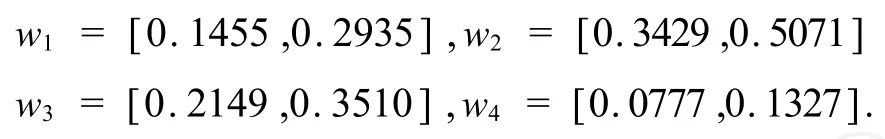
据此可做出判断,企业 X2是最佳的合作伙伴.

4 结 语

在文献[8]的基础上,本文推导出了区间数判断矩阵满意一致性判别方法,并证明了此方法还可以用来判别一致性问题.同时,本文提出的排序向量优化模型,既适用于求解一致性区间数判断矩阵,也适用于求解非一致性区间数判断矩阵.

[1]HainesL.A Statistical Approach to the Analytic Hierarchy Process with Interval Judgments(I) Distributions on Feasible Regions [J].European Journal of Operational Research,1998,110(1): 112-125.

[2]Salo A.On Fuzzy Ratio Comparisons in Hierarchical Decision Models[J].Fuzzy Sets and Systems,1996,84(1):21-32.

[3]Arbel A.Approximate Articulation of Preference and Priority Derivation[J].European Journal of Operational Research,1989,43 (3):126-317.

[4]Satty TL,Vargas L.Uncertainty and Rank Order in the Analytic Hierarchy process[J].European Journal of Operational Research,1987,32(1):107-117.

[5]Wang YM,Yang J B,Xu D L.A Two Stage Logarithmic Goal Programming Method for Generating Weights from Interval Comparison Matrices[J].Fuzzy Sets and Systems,2005,152(1):475 -498.

[6]冯向前,魏翠萍,胡 钢,等.区间数判断矩阵的一致性研究[J].控制与决策,2008,23(2):82-85.

[7]钱 钢,冯向前,魏翠萍.基于一致性指标的两类不确定偏好信息集结[J].控制与决策,2009,24(1):29-34.

[8]Wang YM,Yang J B,Xu D L.Interval Weight Generation Approaches Based on Consistency Test and Interval Comparison Matrices[J].Applied Mathematics and Computation,2005,167(1): 252-273.

[9]Satty T L.The Analysis Hierarchy Process[M].New Y ork: McGraw-Hill Press,1980.

[10]吴 隽,张剑英,任丽娟.基于证据推理与粗集理论的供应链合作伙伴选择方法研究[J].中国软科学,2005,21 (3):130-133.