区间直觉模糊集的包含度的多目标属性决策方法

屈 克,汤 磊,黄建宝

(成都理工大学信息管理学院,四川成都 610059)

0 引 言

1986年,Atanassov[1,2]提出了直觉模糊集的概念,随后又对其进一步的拓展,提出了区间直觉模糊集的概念,并将其运用到多目标属性决策领域中. 2007年,许泽水[3,4]提出了区间直觉模糊的加权平均算子和加权几何算子,为区间直觉模糊信息提供了一种新的决策方法,同时,又进一步地研究并提出了区间直觉模糊的有序加权平均算子和混合平均算子.2007年,胡辉等[5]提出了将TOPSIS方法运用于区间直觉模糊集的多目标属性决策中的方法.本文主要是将文献[6]中的Vague中的包含度拓展到区间直觉模糊集上,并给出了区间直觉模糊集的包含度公式,为区间直觉模糊的多目标属性决策提供一种新的思路.

1 预备知识

定义1.1[2]设 X是一个非空集合,则称,

A={x∈X|([t-A(x),t+A(x)],[f-A(x),f+A(x)])}为区间直觉模糊集.其中,[t-A(x),t+A(x)]、[f-A(x), f+A(x)]⊂[0,1],分别表示隶属度和非隶属度的上下界,x∈X,且 t+A(x)+f+A(x)≤1,∀x∈X,特别的,t-A(x)=t+A(x),且f-A(x)=f+A(x),则区间直觉模糊集退化为直觉模糊集.

定义1.2[2]设A、B是X上的区间直觉模糊集(简写为 IVIFS(X)),则其运算法则为:

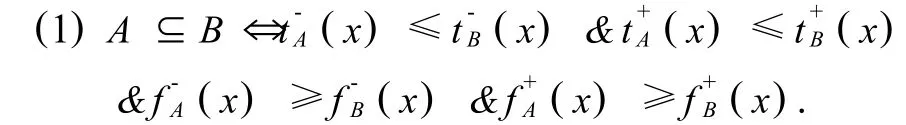
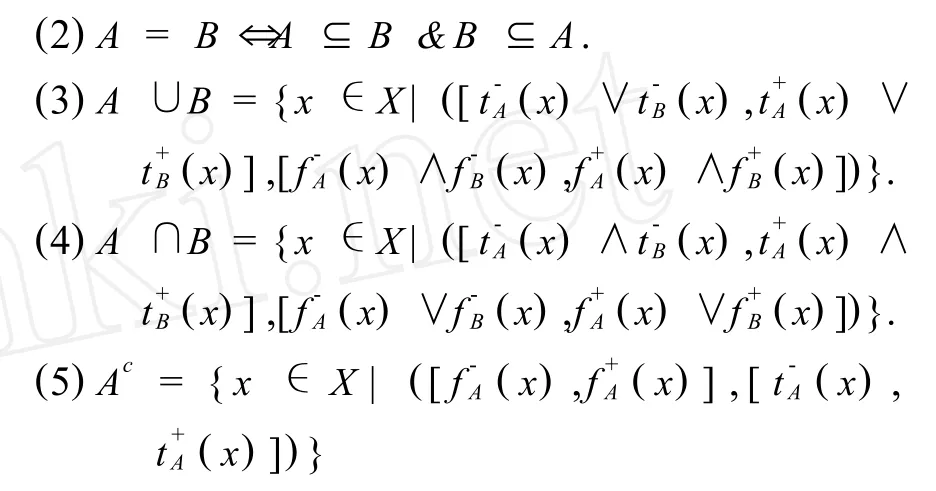
容易验证,(IVIFS(X),⊆)为一偏序集.

2 区间直觉模糊集的包含度

定义2.1 若映射 I:IVIFS(X)×IVIFS(X)→[0,1]满足条件:

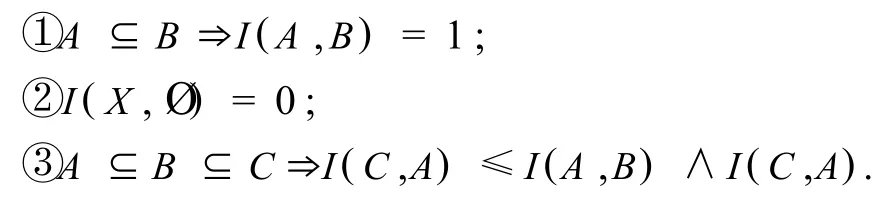
则称I(A,B)为A在B中的包含度,称映射I为包含度函数.

定义2.2[7]若映射θ:[0,1]2→[0,1],满足条件:①θ(1,0)=0;②θ(0,0)=θ(0,1)=θ(1,1).则称θ是模糊正常蕴涵算子,简称正常蕴涵.

设区间直觉模糊集合的全体集为D.

定义2.3[3]设(D,≤)是一子序集,即D上的关系“≤”满足自反性与传递性,且(D,“≤”)上有唯一的最小元素([0,0],[1,1])和最大元素([1,1], [0,0]),称映射D×D→D为T模.若 T满足:对任意的 a,b,c∈D,①交换律 T(a,b)=T(b,a);②结合律 T(T(a,b),c)=T(a,T(b,c));③单调律b≤c,T(a,b)≤T(a,c);④元律 T(a,([1,1][0,0])= a.

定理2.1 设X是一有限论域,θ为一正常蕴涵.

(1)∀u,v∈[0,1],且 u≤v⇒θ(u,v)=1;

(2)θ(u,v)为关于 u的非增函数,θ(u,v)为关于v的非减函数.

则以下 I1,I2均为 IVIFS(X)集的包含度函数.

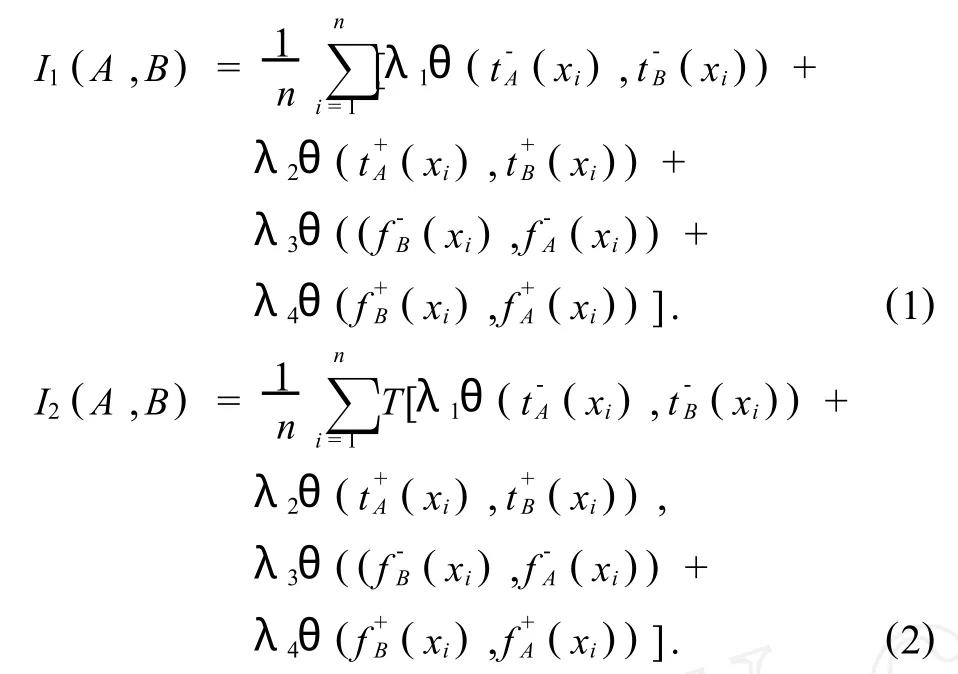
其中,T:[0,1]2→[0,1]为一 T模.且(1)式中的λ1+λ2+λ3+λ4=1,(2)式中的λ1+λ2=1,λ3+λ4=1.

证明 下面仅证 I1,类似可证 I2

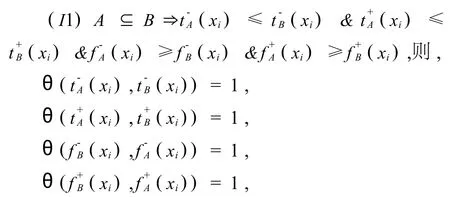
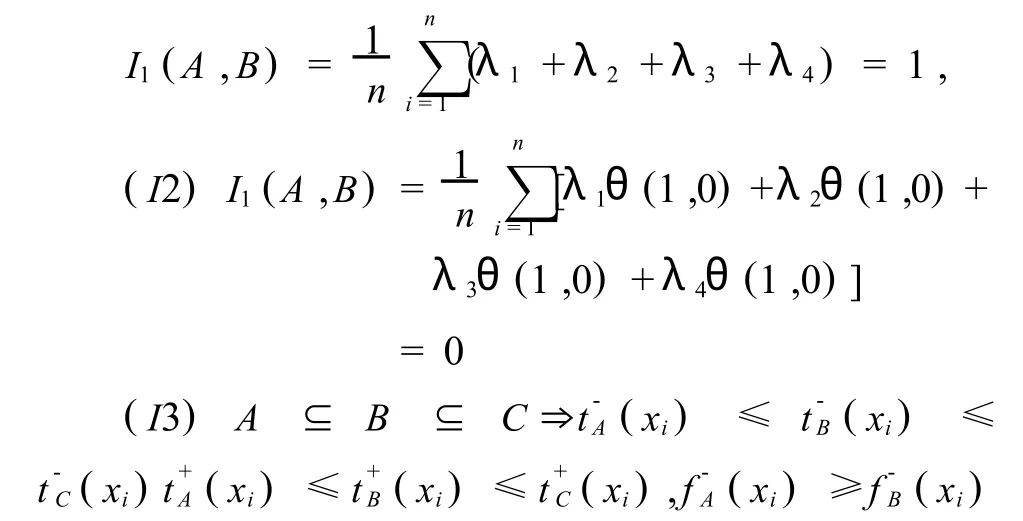
由于θ(u,·)为关于 u递减的,θ(·,v)为关于v递增的,得,

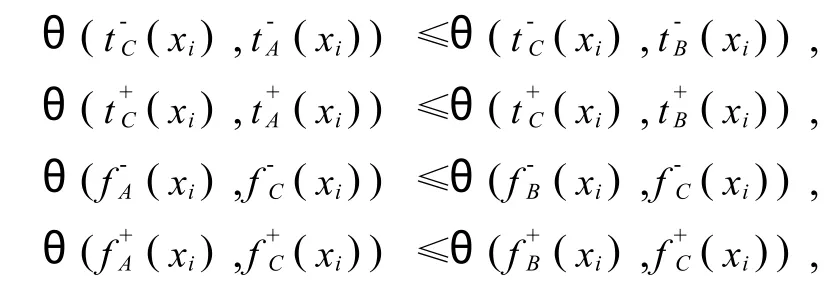
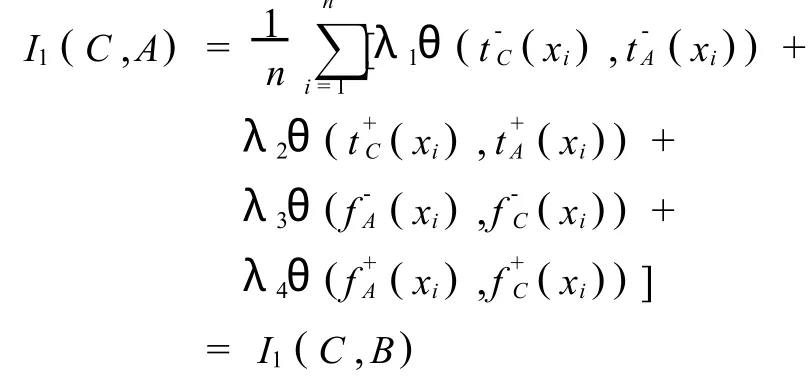
同理即可证:

即,

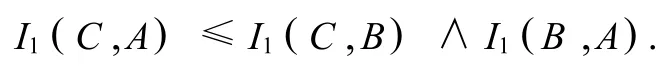
3 基于区间直觉模糊集的模糊多目标决策

设,A为决策方案集,C为目标集,

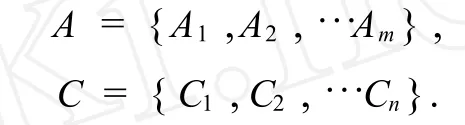
假设决策方案Ai在目标集C下的特征用下列区间直觉模糊集来表示:

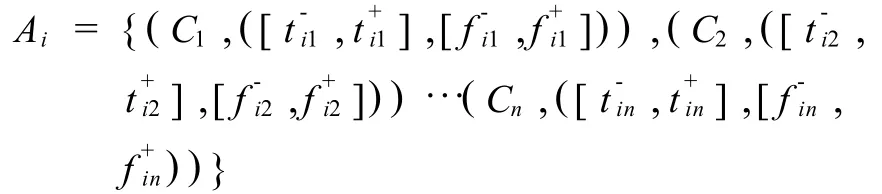
其中,[t-ij,t+ij]为决策方案Ai满意属性Cj的程度区间,[f-ij,f+ij]为不满意属性Cj的程度区间,若决策者要在决策方案集A中选择一个方案使其同时满足属性 Cj,Ck,…Cp或满足Cs,即,Cjand Ck…Cpor Cs.

对该问题现利用区间直觉模糊集的包含度给出目标选择方法.方法的基本思想是先构造理想目标,然后比较理想目标在目标Ai中的包含度,即最大限度地包含理想目标就是最佳目标.

(1)满足约束条件 Cj,Ck…Cp的理想目标,

定义3.1 理想目标在目标方案Ai中的包含度D(Ai)定义为,

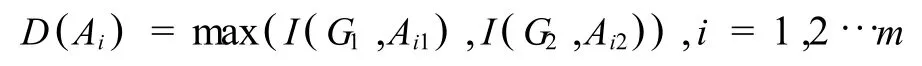
其中,

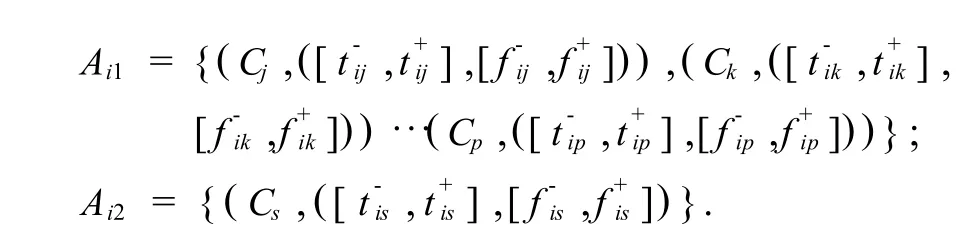
对于上述模糊多目标决策问题的具体算法步骤如下:

(1)分别计算出约束条件 Cj,Ck,…,Cp,或 Cs的理想目标G1与 G2;

(2)计算出 Gj在Aij中的包含度I(Gj,Aij);

(3)计算出理想目标在目标方案Ai中的包含度D(Ai),包含度越大则越好.

例 设决策目标集 A={A1,A2,A3,A4,A5},约束条件集C={C1,C2,C3,C4},决策目标Ai(i= 1,2,3,4,5)在约束条件C下的特征由下列区间直觉模糊集表示(见表1).

表1 决策矩阵

若决策者要在目标集中选择一个同时满足条件 C1,C2,C3或者 C4的最佳方案,其过程如下:

构造满足条件 C1,C2,C3以及 C4的理想目标,

包含度函数 I由定理2.1,取λ1=λ2=λ3= λ4,即,

其中,正常蕴涵θ取Lukasiewica蕴涵,aθb=min{1-a+b,1},∀a,b∈[0,1],求出 Gj在Aij中的包含度I(Gj,Aij)(见表2、表3).

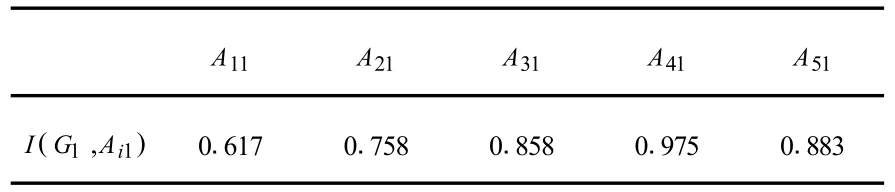
表2 G1在Ai1中的包含度

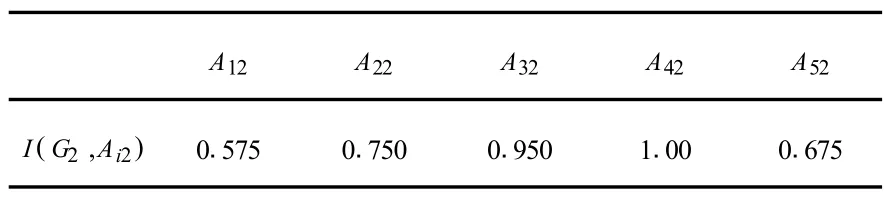
表3 G2在Ai2中的包含度

由此可得出理想目标在目标方案Ai中的包含度D(Ai)(见表4).

由表4可得出:A4≥A3≥A5≥A2≥A1.

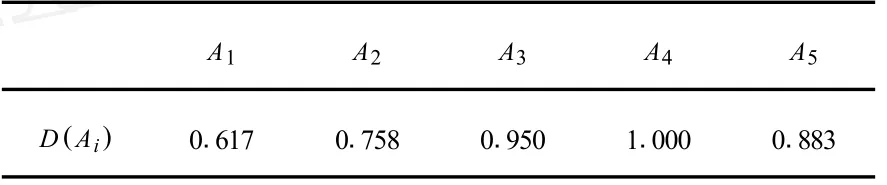
表4 D(Ai)的值

故,A4为最佳目标.

4 结 语

本文将包含度拓展到区间直觉模糊集中,为区间直觉模糊集的多目标属性决策提供了一种新的思路和方法.该方法简洁明了、结构清晰,便于在实际中应用与推广.

[1]Atanassov K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.

[2]Atanassov K,Gargov G.Interval-valued Intuitionistic fuzzy sets [J].Fuzzy Sets and Systems,1989,31(3):343-349.

[3]许泽水.区间直觉模糊信息的集成方法及其在决策中的应用[J].决策与控制,2007,22(2):215-219.

[4]许泽水,陈 剑.一种基于区间直觉判断矩阵的群决策方法[J].系统工程理论与实践,2007,27(4):126-133.

[5]胡 辉,许泽水.基于TOPSIS的区间直觉模糊多属性决策法[J].模糊数学与系统,2007,21(5):108-111.

[6]刘华文.基于Vague集包含度的模糊多属性决策[J].中国管理科学,2004,12(4):89-91.

[7]吴望名.模糊推理的原理与方法[M].贵阳:贵州科技出版社,1994.