用数学建模方法解决哥尼斯堡七桥问题

高中印

(承德民族师专 数学与计算机系，河北 承德 067000)

用数学建模方法解决哥尼斯堡七桥问题

高中印

(承德民族师专 数学与计算机系，河北 承德 067000)

作者介绍了七桥问题的由来，以及用数学建模方法来解决七桥问题。这为我们中学数学建模提供了又一经典范例。

七桥问题；问题解决；经典范例

数学建模方法是把实际问题抽象成数学模型，也就是把实际问题转化成数学问题，然后再用数学的方法加以解决。哥尼斯堡七桥问题的研究就是数学建模中的一个经典。

一、哥尼斯堡七桥问题的由来

哥尼斯堡就是现在的俄罗斯的加里宁格勒。哥尼斯堡在第二次世界大战前属于德国，是东普鲁士的首府，在历史上，哥尼斯堡的归属曾发生过几次变化。二战结束后，根据雅尔塔和波斯坦协议，东普鲁士部分领土划归苏联，是苏联作为战胜国享受的战利品。苏联把哥尼斯堡更名为加里宁格勒。斯大林没有把加里宁格勒划入刚刚并如苏联的立陶宛，而是划入俄罗斯联邦。加里宁格勒风景秀丽，气候宜人。这里有着丰富的自然资源，是重要的军事基地，也是重要的海运港口。1991年苏联解体，波罗的海周边三国的立陶宛、拉脱维亚和爱沙尼亚独立，加里宁格勒就变成了俄罗斯的一块飞地。

普莱格尔河（Pregel）穿过美丽的哥尼斯堡城。普莱格尔河有两个支流，在城市中心汇成大河，中间是岛区，人们在河上建起了七座桥，使这里成为风景优美的人间仙境，如图1所示。

由于岛上有古老的哥尼斯堡大学，有知名的教堂，有大哲学家康德的墓地和塑像，因此城中的居民，尤其是大学生们经常到河岸和上桥散步。在十八世纪初，有一天，有人突发奇想：如何才能走过七座桥，而每座桥都只能经过一次，最后又回到原来的出发点？当地的人们开始沉迷于这个问题，在桥上来来回回不知走了多少次，然而却始终不得其解，这就是著名的哥尼斯堡七桥问题的由来。

二、大数学家欧拉的数学建模

哥尼斯堡七桥问题看起来似乎很简单，其实很多人经过多次尝试，却始终没有找到答案。这个问题很快传到了欧洲，成了著名的数学难题。

大数学家欧拉（Euler）此时受俄国之邀，正在圣彼得堡科学院做研究。他的德国朋友告诉了他七桥问题，引起了欧拉的极大兴趣。他想：经过这么多人的努力都找不到不重复的一次走完七座桥的路径，会不会是这样的走法根本不存在？但是这只是个猜想，还需要证明。

欧拉首先想到的是用穷举法，就是把所有的走法都一一列出来，然后再一个一个的验证是否可行。但是他马上发现这样做太麻烦了，因为对七座桥的不同走法就有7！=5040种，逐一检验太耗时费力了，况且这样的方法没有通用性。如果桥的位置或桥的数量发生变化，岂不又得重新检验？看来此法不可行。

经过反复思考，欧拉想到：岛的形状、大小、以及桥的长短、宽窄并不影响结果，位置才是最重要的。于是他联想到了莱布尼兹(Leibniz)的位置几何学，既然陆地是桥梁的连接地点，不妨把图中被河隔开的4块陆地看成4个点，7座桥看成7条连接这4个点的线，这样将图形简化，于是就画了如图2的图形。

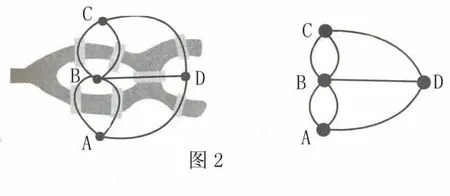
七桥问题就相当于一笔画出此图形的问题。这是把陆地（平面）用点来表示，把桥用线来表示。多么美妙的构思啊！这就是数学大师欧拉对七座桥问题建立起来的数学模型。

三、七桥问题的最终解决

通过数学建模，已经把实际问题转化成了数学问题。这时欧拉注意到，如果一个图形能一笔画成，那么除去起点和终点外，其他的点都是经过点。而经过点是有进有出的点，即有一条线进这个点，就一定有一条线出这个点。不可能有进无出，如果有进无出，它就是终点；也不可能有出无进，如果有出无进，它就是起点。因此，在经过点进出的线总数应该是偶数。我们称在一个点进出线的总数是偶数的点为偶点；总数为奇数的点称为奇点。如果起点和终点是同一个点，那么它也属于有进有出的点，它也是偶点，这样图上的点全是偶点。如果起点和终点不是同一个点，那么它们必定是奇点。因此，能够一笔画的图形最多只有两个奇点。

1736年，欧拉证明了自己的猜想，一次不重复走完七座桥是根本不可能的。随即他发表了“一笔画定理”：

一个图形要能一笔画完，必须符合以下两个条件：

（1）图形是封闭连通的；

（2）图形中的奇点个数为0或2；

七桥问题中的四个点全是奇点，当然不能一笔画，即不可能一次无重复地走完七座桥。一般地说，如果图中的点全是偶点，那么可以任意选择一个点作为起点，当然终点与起点重合，能一笔画成；如果图中有两个奇点，那么可以任意选一个奇点作为起点，另一个奇点为终点，可以一笔画成。

欧拉的这个研究成果，开创了图论和拓扑学这两门新的学科。这两门学科在计算机科学中有着广泛的应用。由此可见，只要善于用数学的眼光、数学的方法去观察事物，分析问题，就能把生活中的一些实际问题转化为数学问题，并用数学的方法来处理和解决。欧拉用数学建模的方法来解决七桥问题，可以说为我们中学数学建模提供了又一经典范例。

[1]姜启源.数学建模[M].北京：高等教育出版社，1993.

[2]唐越桥.中学数学创新实验[M].南宁：广西教育出版社，2006.

[3]李文林.数学史[M].北京：高等教育出版社，2004.

O12

A

1005-1554（2010）02-0014-02

2010-02-05

高中印（1956-），男，河北承德人，承德民族师专数学与计算机系教授。