自调匀整模糊控制系统设计及FPGA实现
2010-01-09朱耀麟李兰君王延年
朱耀麟,李兰君,张 涛,王延年
(西安工程大学 电子信息学院,西安 710048)
自调匀整模糊控制系统设计及FPGA实现
朱耀麟,李兰君,张 涛,王延年
(西安工程大学 电子信息学院,西安 710048)
针对自调匀整系统控制过程复杂、难以建立精确模型的特点,设计了基于现场调试经验的模糊控制算法.为了提高控制性能,采用常规PID与模糊控制相结合的方法.在Altera公司提供的QuartusII开发环境中,利用原理图设计和VHDL设计输入相结合的方式,在FPGA上实现了模糊PID控制算法.根据仿真结果分析,该设计实现了模糊PID控制功能.
自调匀整;模糊控制;FPGA;模糊自整定PID控制器
自调匀整是一种用来控制纱条粗细不匀的自动调节装置,它在现代纺织工业中有着极其重要的地位.该系统是一个强扰动(输入棉条线密度不断变化)、大延迟(匀整点到检测点的延时)的定值(输出棉条的线密度为一定值)系统[1].传统的PID控制方法主要适用于线性控制过程,对于这种滞后比较严重的被控对象控制效果较差.由于自调匀整系统具有非线性、时变性、不确定性的特点,难以建立精确的数学模型,采用经典控制理论中的PI和PID控制规律很难获得满意的效果.而模糊控制不需要控制对象的精确数学模型,它是一种基于规则的控制,依据操作人员的控制经验和专家知识,通过查表就可以得到控制量,实现简单,控制效果好.模糊控制尤其适用于数学模型未知、复杂的非线性系统的控制.采用模糊推理的方法实现PID参数kp、ki、kd的在线自整定,不仅保持了常规PID控制系统原理简单、使用方便、鲁棒性较强等优点,而且具有更大的灵活性,整定性、控制精度更好,是目前较为先进的一种控制系统.分析表明,基于模糊控制与常规PID结合是提高控制性能的有效手段[2].姚杰等[3]分析了高速并条机短片段自调匀整装置,开发出基于开环控制的、带有双自调因子与量化因子优化相结合的智能型模糊控制器.Yueyang guo[4]在梳棉机上运用一套通用可预测理论进行自调匀整,得出了控制模型.李洪兴[5-6]从模糊控制的插值机理出发,揭示出模糊控制器的本质是某种插值器,并介绍了基于论域收缩的一类模糊控制器的设计思想.无论是梳棉机还是并条机,其静态数学模型都比较简单,但设计高质量的能适应高速的自调匀整系统,仅有静态数学模型还远远不够,必须建立能用于控制工程的动态模型.本文从匀整理论入手,结合现代计算机控制理论,主要研究自调匀整机构的实现方案和匀整控制理论,并应用理论设计一种在梳棉机上使用的自调匀整机构.
1 自调匀整系统的数学模型及传统控制方法
自调匀整装置按其控制形式可分为开环、闭环和混合环.混合环是开环和闭环的混合形式,它将快速反应的开环系统与中、低速反应的闭环系统有机结合起来,在控制机构上叠加两方面检测到的讯号,取长补短,使棉条的短中长片段均匀度得到改善.图1为自调匀整混合环控制系统结构图.
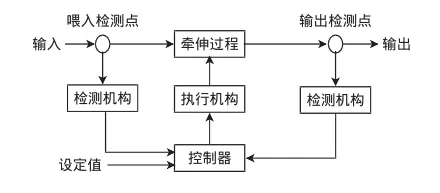
图1 自调匀整混合环控制系统Fig.1 Hybrid loop autoleveller system
由梳棉机的特性,梳棉机的数学模型为[7]:
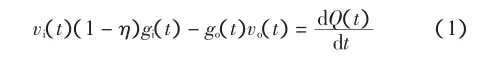
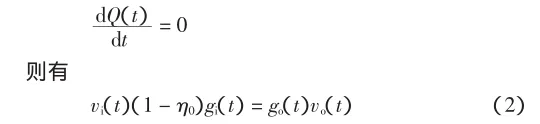
梳棉机自调匀整装置的目的就是使输出条子均匀,即go(t)=gos,gos为输出生条线密度的设定值.由式(2)可得控制律为:
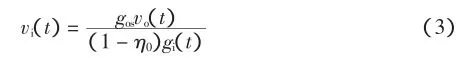
式中:η为落棉率;gi(t)为喂入棉层线密度(g/m);go(t)为输出生条线密度(g/m);vi(t)为喂入棉层线速率(m/ s);vo(t)为输出棉层线速率(m/s);Q(t)为梳棉机内纤维存量(g/m).设落棉率不变为η0,且梳棉机内棉纤维存储量基本不变,即
实际生产中很难精确检测线密度的变化,通常在梳棉机上检测到的是输入棉层厚度和输出棉条的粗细,然后通过调节罗拉的牵伸倍数达到使输出棉条均匀的目的.自调匀整系统复杂,且由于落棉率等一些未知因素的影响,要得到精确的数学模型十分困难,且传统的PID控制有惯性滞后的影响.因此,使用模糊理论对本系统进行控制是十分合适的.
2 自调匀整的模糊自整定PID算法
模糊自整定PID是在PID算法的基础上,通过计算当前系统误差e和误差变化率ec,利用模糊控制规则进行模糊推理,查询模糊矩阵表进行参数调整.模糊自整定PID控制器的离散表达形式如下[8]:
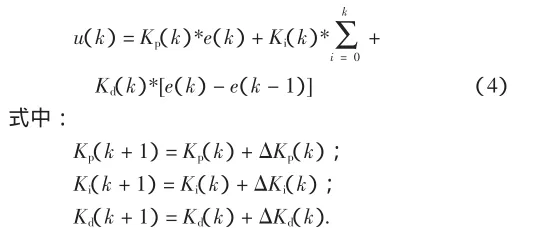
模糊自整定PID控制器以误差e和误差变化量ec作为输入,可以满足不同时刻的e和ec对PID参数自整定的要求.利用模糊控制规则在线对PID参数进行修改,便构成了自适应模糊PID控制器,其结构如图2所示[9].
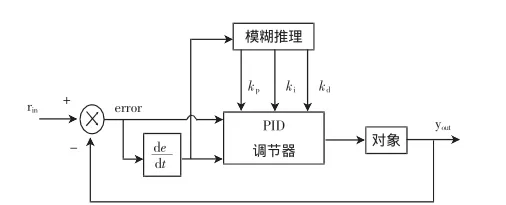
图2 自适应模糊控制器结构Fig.2 Structure of fuzzy self-tuning PID controller
PID参数模糊自整定是找出PID的3个参数与e和ec之间的模糊关系,在运行中通过不断检测e和ec,根据模糊控制原理对3个参数进行在线修改,以满足不同e和ec时对控制参数的不同要求,而使被控对象有良好的动、静态性能.
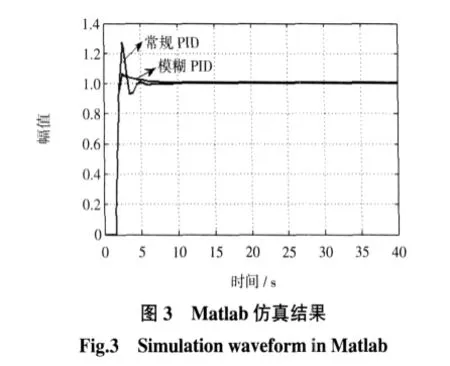
由图3仿真结果可知,常规PID和模糊PID的响应速度、稳定性相当,但是常规PID的超调量为28%,而模糊PID的超调量只有7%,与常规PID相比,模糊PID的超调量更小.
3 模糊PID算法的FPGA实现
模糊控制策略较为理想的实现方式是基于硬件,因此,本文选择FPGA实现模糊自整定PID算法.FPGA最明显的优势在于集成度高、体积小、功耗低、可靠性高、电路设计灵活.通过FPGA技术来实现模糊PID算法控制,把系统的硬件和软件充分结合,可扬长避短,使其最大限度地发挥各自的优点,使得硬件的成本降到最低;同时保证了系统算法模块的简化,减少了处理器对算法的运算,提高了系统的运行速度,在复杂的控制系统中,可以大大地减轻处理器的负担,为算法的优化提供可行的方式;大大降低了由于计算机故障对控制系统的影响,提高了控制模块的可靠性.图4为基于FPGA的模糊自整定PID控制器电路架构.
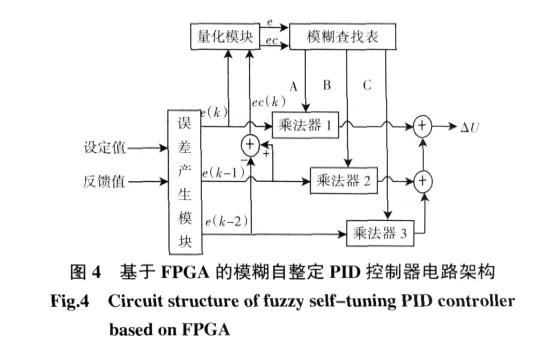
系统分为4个模块:误差产生模块、量化模块、模糊查找表模块以及乘加模块.误差产生模块生成误差(设定值和反馈值的差值)和误差变化率的精确值;量化模块是将误差和误差变化率的精确值量化成为模糊值;该模糊值作为模糊查找表的输入,经模糊查找表之后输出PID参数的值,经乘加运算后输出控制量U值.
3.1 误差及误差变化量模块的设计
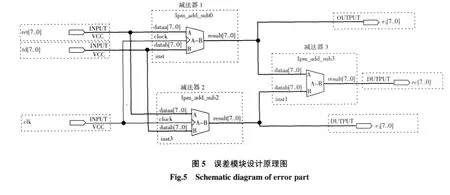
模糊PID算法的输入是误差及其误差的变化率,误差是设定值与反馈值的差值,根据前后两次误差量可以得出误差变化率.在离散化论域中,将当前周期的误差量与上一个周期的误差量进行比较产生误差变化量,利用误差变化量的值来代替误差变化率.本模块的设计通过QuartusII模块库中的LPM_ADD_SUB来实现,但只采用了此模块的减法功能[10].图5为误差模块设计原理图.
3.2 模糊量化等级模块的设计
误差和误差变化量模块输出的是精确值,而模糊控制器的输入必须是经过量化后的模糊值.因此,精确值需经模糊量化后才能作为模糊控制器的输入.此模块的基本思想是:首先将模糊论域范围内输入的精确量进行量化,使其符合论域范围;将模糊论域按基本元素的不同分为若干段,每一段对应于一个论域中的基本元素.当输入精确值落入某个论域范围段时,经过模糊量化后,对应此精确量的输出量即为此论域的基本元素值.本文中将误差大小量化为7个等级,基本论域范围为[-30,30],量化因子为10,采用四舍五入的方法,将基本论域分为7段.利用QuartusII里LPM_COMPARE函数实现精确值与量化值的比较,量化后再通过一片74148对量化值进行编码,使每一个量化值都对应一个编码.假设误差的精确值是12,此精确值在[5,15)的论域段,那么误差的量化值就是1. ec和e的量化过程相同,表1为e/ec的量化地址.

表1 模糊量化后e/ec的量化地址Tab.1 Fuzzy address of e/ec
3.3 模糊查找表模块
模糊查找表是模糊控制器的核心[11],本文采用离线计算得到的控制表来代替模糊化运算、模糊推理和清晰化计算等一系列复杂的工作,而且在实际控制时在线运算量很少.这种离线计算、在线查表的方法大大提高了FPGA的工作效率,而且降低了编程难度.
Matlab的模糊逻辑工具箱提供了建立和测试模糊逻辑系统的一整套功能函数,包括定义语义变量及隶属度函数、建立模糊推理规则、整个模糊推理系统的管理以及交互式地观察模糊推理过程和推理结果.考虑到e和ec都是经过量化的值,即模糊输入的论域是离散的,这就意味着输入量e和ec的数目是有限的,可以在Matlab中建立该模糊逻辑函数的模型,把所有e和ec的组合输入模糊推理模型里,求出在这些输入下kp、ki和kd的值.为进一步降低计算复杂度,可设变量
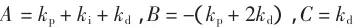
即对kp、ki和kd的值进行线性组合,可以制作出一份以e、ec为输入,以A、B、C为输出的控制表.其中高3位是误差e的量化地址,低3位是误差变化率ec的量化地址.将A、B、C表在QuartusII里制作成.mif文件,分别放入3个ROM里.那么在FPGA上要完成的工作就只剩下计算:

3.4 乘法模块和加法模块
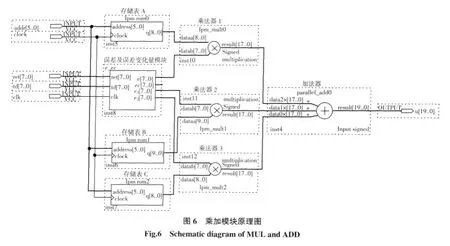
乘法模块调用了函数库里的LPM_MULT实现A与e(k)、B与e(k-1)、C与e(k-2)的相乘,然后调用parallel_add将3个值相加得到控制量Δu.图6为乘加模块原理图.
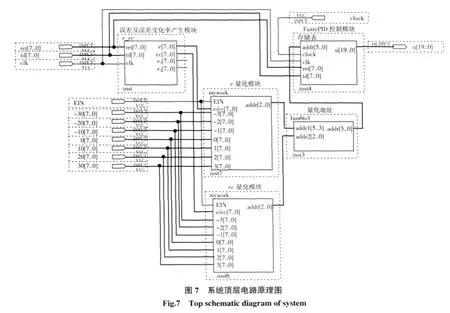
3.5 系统顶层电路原理图及其仿真
系统顶层电路原理图如图7所示.
取一组数据,令ret=21,td=30,那么误差精确值e=-9,e1=-9,e2=-16,误差变化量的精确值ec=7,精确值e属于[5,15)论域段,其量化值是-1,量化编码010.同理可知ec的量化编码100.将e的量化编码作为高3位,ec的量化编码作为低3位,查表可知A=-110,B=219,C=-109,由(5)式计算可得U=763.仿
真结果如图8所示.
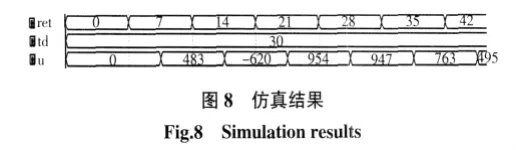
由图8可以看出,仿真与计算结果相同,证明了系统整体设计的正确性,说明此种方法切实可行.
4 结束语
与传统PID控制相比,模糊控制更适用于大滞后、非线性的复杂系统.因此,本文提出用模糊控制方法对自调匀整系统进行控制,使用Altera的FPGA设计实现了模糊自整定PID控制器,设计采用离线计算、在线查表的模糊自整定参数技术和增量式PID算法.仿真结果显示,本设计既降低了FPGA的资源耗费,又改善了传统PID控制器的控制性能,设计方案可行.
[1]郭月洋,陈瑞琪.棉纺设备自调匀整系统发展方向的探讨[J].棉纺织技术,2002,30(5):29-32.
[2]王化祥.一种新型模糊PID调节器的设计[J].自动化仪表,2000,21(5):8-10.
[3] 姚 杰,叶国铭.新型开环自调匀整装置的分析与设计[J].纺织学报,2005,26(3):44-45.
[4] GUO Yueyang.Applying a generalized predictive control theory to a carding autoleveler[J].Textile Res J,2003,73(9):755-761.
[5] 李洪兴.Fuzzy控制的本质与一类高精度Fuzzy控制器的设计[J].控制理论与应用,1995,14(6):868-872.
[6] LI Hongxing,CHEN C L Philip.Relationship between fuzzy controller and PID controller[J].Science in China:Series E,1999,42(2):215-224.
[7] 曾光奇,胡均安,王 东,等.模糊控制理论与工程应用[M].武昌:华中科技大学出版社,2006.
[8] 谢仕宏.MATLABR2008控制系统动态仿真实例教程[M].北京:化学工业出版社,2009.
[9]刘金琨.先进PID控制MATLAB仿真[M].北京:电子工业出版社,2004.
[10]王军伟.基于FPGA的模糊PID控制算法的研究及实现[D].杭州:浙江工业大学,2009.
[11]李昌武,彭良玉.模糊自整定PID控制器的FPGA实现[J].现代电子技术,2007,256(17):116-121.
Design of fuzzy control system in autoleveller based on FPGA
ZHU Yao-lin,LI Lan-jun,ZHANG Tao,WANG Yan-nian
(Electronic Information College,Xi′an Polytechnic University,Xi′an 710048,China)
According to the speciality of complex controlling rule and difficult building of system model,a fuzzy controller based on experiences is designed.In order to improve control performance,the traditional PID is combined with fuzzy control method.The fuzzy PID control algorithm is implemented on FPGA by using the hierarchical modular design and combining the schematic design method with VHDL design method in the QuartusII development environment provided by Altera.According to the result of the simulation analysis,the control chip achieves the desired function of fuzzy PID control algorithm.
autoleveller;fuzzy control;FPGA;fuzzy self-tuning PID controller
TS103.113;TP29
A
1671-024X(2010)06-0063-05
2010-08-30
朱耀麟(1977—),男,博士,副教授,硕士生导师.
朱耀麟(1977—),男,博士,副教授,硕士生导师.E-mail:fz_zyl@126.com
·科研鉴定·
