两级封闭行星齿轮传动系统的设计研究

段福海 钟 勇



两级封闭行星齿轮传动系统的设计研究

段福海 钟 勇

福建工程学院机电及自动化工程系

通过对两类两级封闭行星齿轮传动系统的分析，研究了功率分配系数与系统内部功率流的关系，确定了无功率循环的必要条件，建立了功率分配系数与单元传动比的关系表达式以及效率计算公式。通过分析结合实例绘出的传动比和效率曲线图，说明只要合理地选择单元传动比便可获得高效率的传动，为两级封闭行星齿轮传动系统的高效率设计提供一种有效简洁的分析和处理方法。

行星齿轮 效率 功率流

两级封闭行星齿轮传动系统若在两条传递路径上分配输入功率，则通过双路径传动使其构件上转矩减小，在传递相同载荷条件下结构更加紧凑；另外，通过速度合成，扩大了传动比选择范围，可灵活地选择传动比，尤其对一些严格要求传动比的场合，可精确地得到传动比，如航空加法传动[1]。由于封闭行星齿轮传动的上述优点,广泛地应用于工业机械、起重机械、建筑机械、冶金机械以及航空机械等现代机械传动领域。另外，由于封闭行星齿轮传动可以进行多个动力源的功率分流与汇流、结构紧凑，使其在混合动力车辆传动系统得到了广泛应用，如艾里逊油电混合器、丰田普锐斯的油电混合系统。

每对齿轮副所传递的功率取决于齿数比和轮系结构，即轮系结构和齿数比决定着齿轮副的功率流。然而，如果封闭行星齿轮传动系统各支路的传动比选择不当，将会使其内部存在较大的循环功率[2-6]（封闭功率）。循环功率的存在加大了构件上的载荷,加剧了磨损，产生较大的振动和噪音，严重降低了传动系统的性能。文中通过对两级封闭行星齿轮传动系统的功率流分析，说明合理地选择单元传动比可获得高效率的传动，介绍一种避免功率循环的单元传动比配置方法。

1 两级行星齿轮传动系统

简单的单级行星齿轮传动系统有3个运动的基本构件，为两自由度系统。通过接入一个控制元件，制动一个构件或者使2个构件刚性连接，使其成为具有确定运动的单自由度系统，因此，可通过给定一个构件的运动来实现对其它构件运动的控制[2]。

两级行星齿轮传动系统具有四个自由度，需要接入3个控制元件来形成单自由度传动系统，其中，3个控制元件可以选择性地制动某些构件或者刚性连接某些构件。当构件刚性连接时，其上所产生的转矩和速度直接决定着输入功率在内部路径上的分配，以及在内部路径上的循环。

如表1中(a)所示，若将两个简单的单级行星齿轮传动相互串连，则可形成两级行星齿轮传动系统，不考虑损失，输入功率流经每一个单元（构件A 、B、d、e分别为输入、输出、连接、制动构件）。

如表1(b)(c)所示，若将一个简单的单级行星齿轮传动系统与一个差动行星齿轮传动系统进行封闭式连接，就形成了两级封闭行星齿轮传动系统，其中只有一个固定构件，单元间通过构件刚性连接。很明显，(b)中输入功率in在1利用双路径传递，其中一部分功率1通过2传递给输出轴，另一部分功率2绕过2传递给输出轴。(c)中输入功率in在1利用两条路径传递，其中一部分功率1通过1传递给2，另一部分功率2直接传递给2，然后在2处汇流输出。所有的两级行星齿轮传动系统的连接都可简化为表1结构简图的形式。文中只考虑表1中(b)、(c)具有功率分流形式的两级封闭行星齿轮传动系统。

2 运动学关系

表1(b)中转矩和功率由两条路径输出，称为功率分流输出型两级封闭行星齿轮传动系统；表1(c)中转矩和功率由两条路径输入，称为功率分流输入型两级封闭行星齿轮传动系统[6]。二者广泛地应用于动力传动系统中，文中主要以二者为研究对象。传动系统内将给定方向上功率流定义为正方向，若实际功率流方向与定义的方向相同，则为正；反之，则为负。因此，需要通过计算来判定实际功率流的正负号。

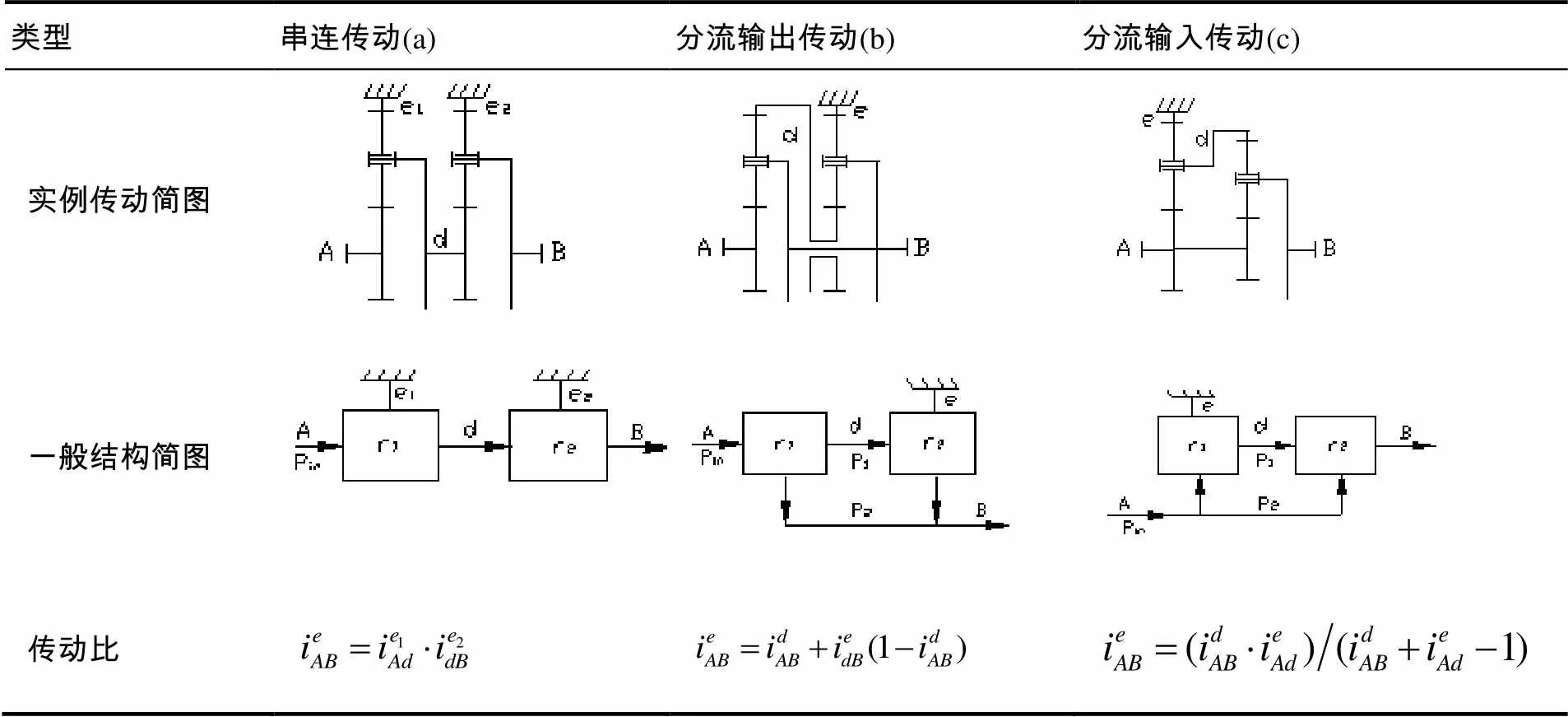
表1 两级行星齿轮传动系统

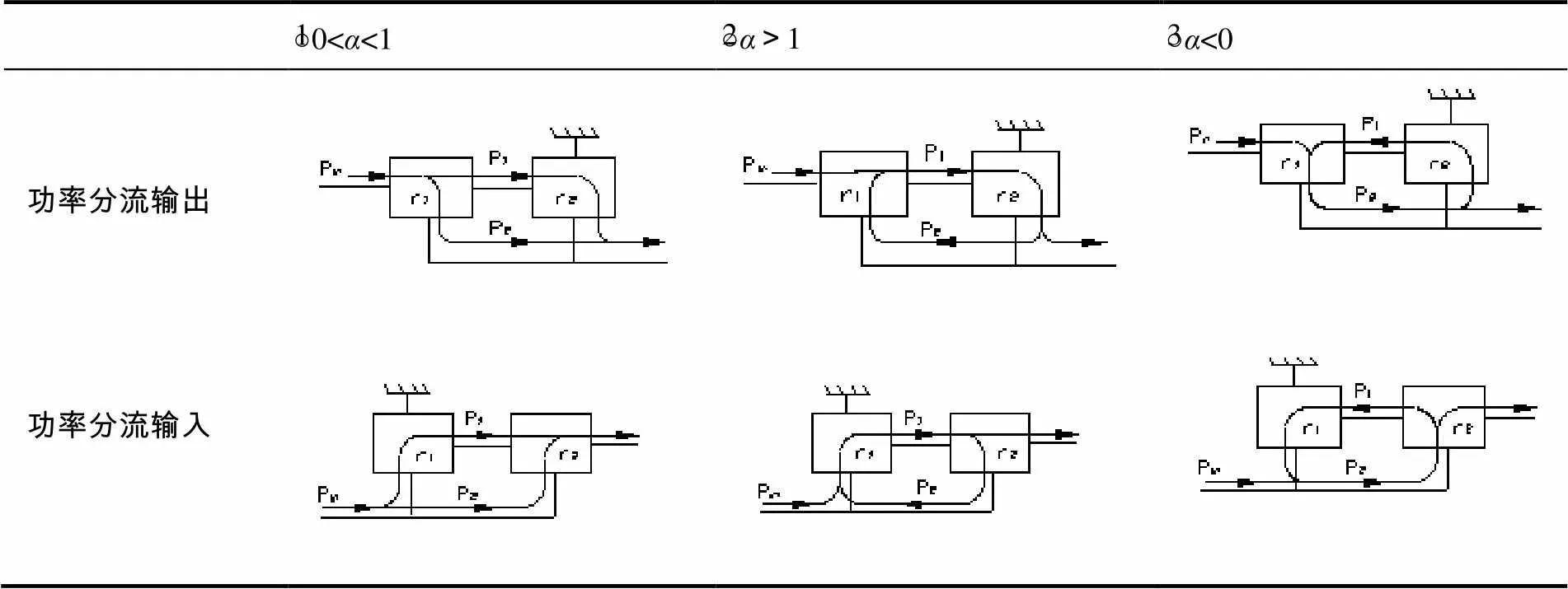
表2 两级封闭行星齿轮传动系统内部功率流方向

定义：传动比为传动系统的输出转速与输入转速之比；单元传动比1为制动连接构件时，输出转速与输入转速之比；单元传动比2为固定构件时，连接构件转速与输入转速之比（功率分流输入型）或输出转速与连接构件转速之比（功率分流输出型）。

系统输入功率与各支路传递功率的关系

in=1+2（1）

支路传递功率为1=dd（2）

式中d、d分别为连接构件的转矩和转速。

是输入功率在各支路上的分配系数，二者满足

表1(b)中传动比和功率分配系数与单元传动比的关系式

构件d的转矩和转速为

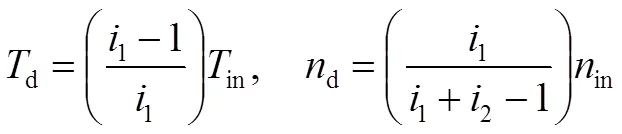
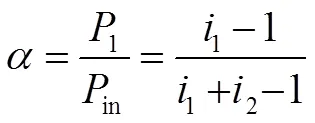
表1(c)中传动比和功率分配系数与单元传动比的关系式

构件d的转矩和转速为

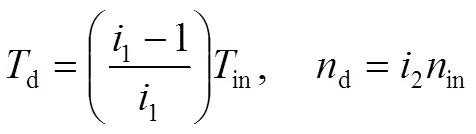
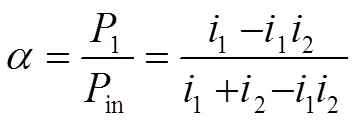
3 系统功率流

两级封闭行星齿轮传动系统内环路出现功率循环将会增加轮齿和轴承上载荷，加剧磨损，从而使其传动效率降低[1]。通过以上分析可知，功率分配系数是单元传动比的函数，单元传动比决定着输入功率在支路上的分配和有无功率循环，因此，通过合理地选择单元传动比1、2，便可实现传动系统无功率循环传动，其必要条件为

4 系统效率分析

文献[1]对传动比与效率的关系定义如下：如果运动传动比（忽略功率损失）取功率流方向的话，那么动力传动比（考虑功率损失）为运动传动比乘以效率；如果运动传动比与功率流方向相反，则动力传动比为运动传动比乘以效率倒数-1，这种理论对于复杂传动也正确。从表2中可以看出，功率1流经两个行星齿轮传动单元，功率2流经一个行星齿轮传动单元。设每个传动单元转臂固定时的效率分别为1、2，只考虑由轮齿间摩擦引起的损失，一般取值为1＝2＝0.96。则两级封闭行星齿轮传动系统传动效率AB的计算公式

由式(14)、(15)可得

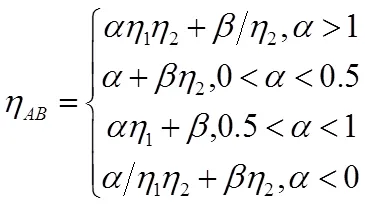
5 实例

图1(1)、(2)为功率分流输出型传动结构，图1(3) 、1(4)为功率分流输入型传动结构，其各齿轮齿数如表3中所示，

图1 封闭行星齿轮传动结构

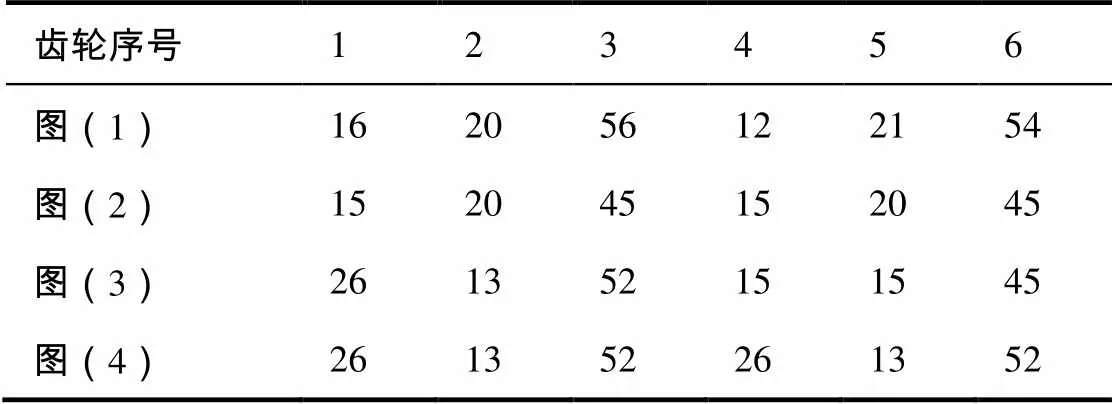
表3 封闭行星齿轮传动系统各齿轮齿数

运动学计算如下：

图1（1）

图1（2）

图1（3）

图1（4）

6 图解说明与分析

结合上述实例，以单元传动比1为横坐标，2为纵坐标，通过给定的传动比，根据公式(5)、(9)建立1与2的函数关系式，并绘出其函数图像，在图中以细实线表示；根据公式(7)、(11)、(12)、(13)，建立与1、2的函数关系式，绘出函数图像，在图中以点划线表示，这些点划线将坐标系划分为无功率循环区、正功率循环区和负功率循环区；在上述基础上，根据公式(16)，建立了系统传动效率AB与功率分配系数的函数关系式，绘出函数图像，在图中以虚线表示。

从图2中可以看出传动比=-0.067的曲线有两支，一支分布在无功率循环区，另一支则分布在功率循环区。曲线上的每一点对应的i、i都满足=-0.067，因此，除传动比约束外，若不考虑其它约束条件，则1、2有无数种选择方案。结合效率曲线可以看出，若1、2在无功率循环区曲线上取值，其效率曲线0<α<1变化平缓且非常接近1，说明传动效率很高；若1、2在功率循环区曲线上取值，其效率曲线η>1、η<0发生显著变化，特别在正负功率循环转变区域附近其急剧变化，传动效率非常低。

实例图1(1)对应的点为m，该点位于正功率循环区，传动效率η=0.884。由于该方案传动效率较低，为获得较高效率的传动，根据前述功率流图解分析理论可知，需要在无功率循环区传动比曲线上选点，通过调整构件连接和齿轮齿数，即实例图1(2)，得到点，该点对应的传动效率为=0.967。

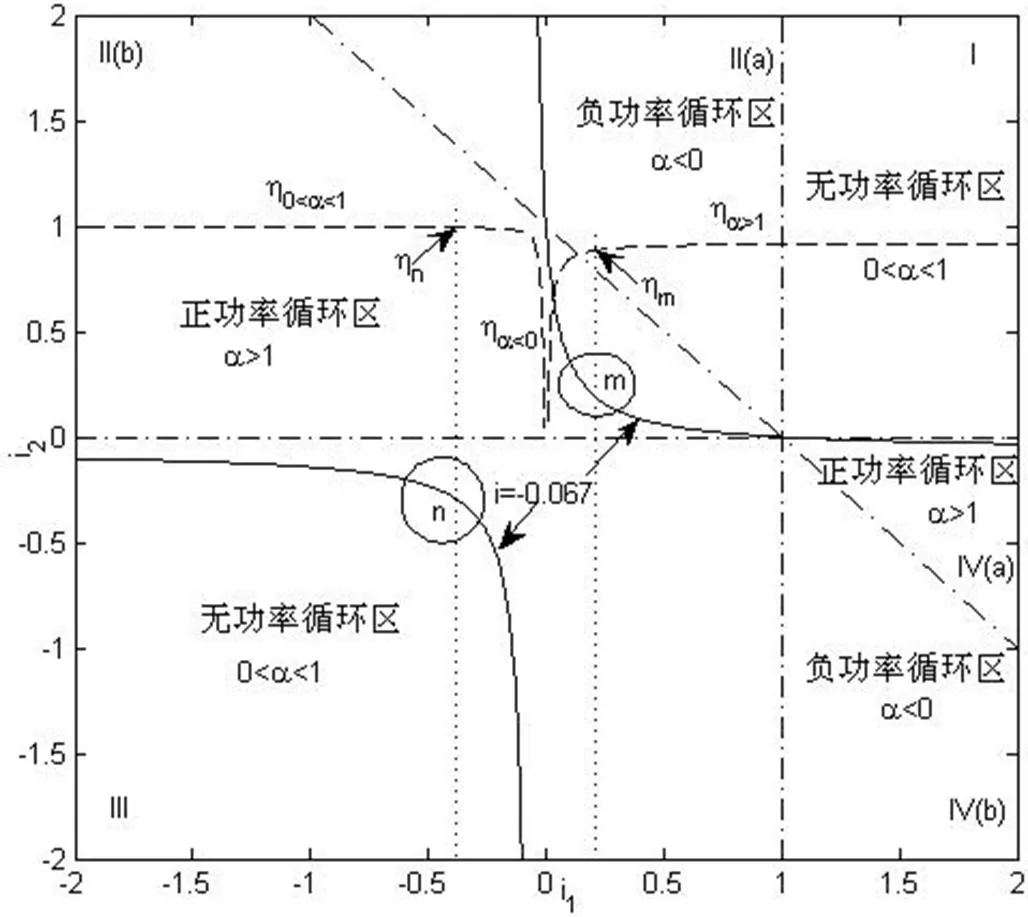
图2 功率分流输出型传动比及效率曲线图

从图3中可以看出传动比=0.555的曲线只有一支，该曲线分布在正功率循环、无功率循环和负功率循环三个区域。同样，曲线上的每一点对应的1、2都满足=0.555。结合效率曲线可以看出，由于该曲线不存在正负功率循环的转变区域，其效率曲线变化比较平缓。

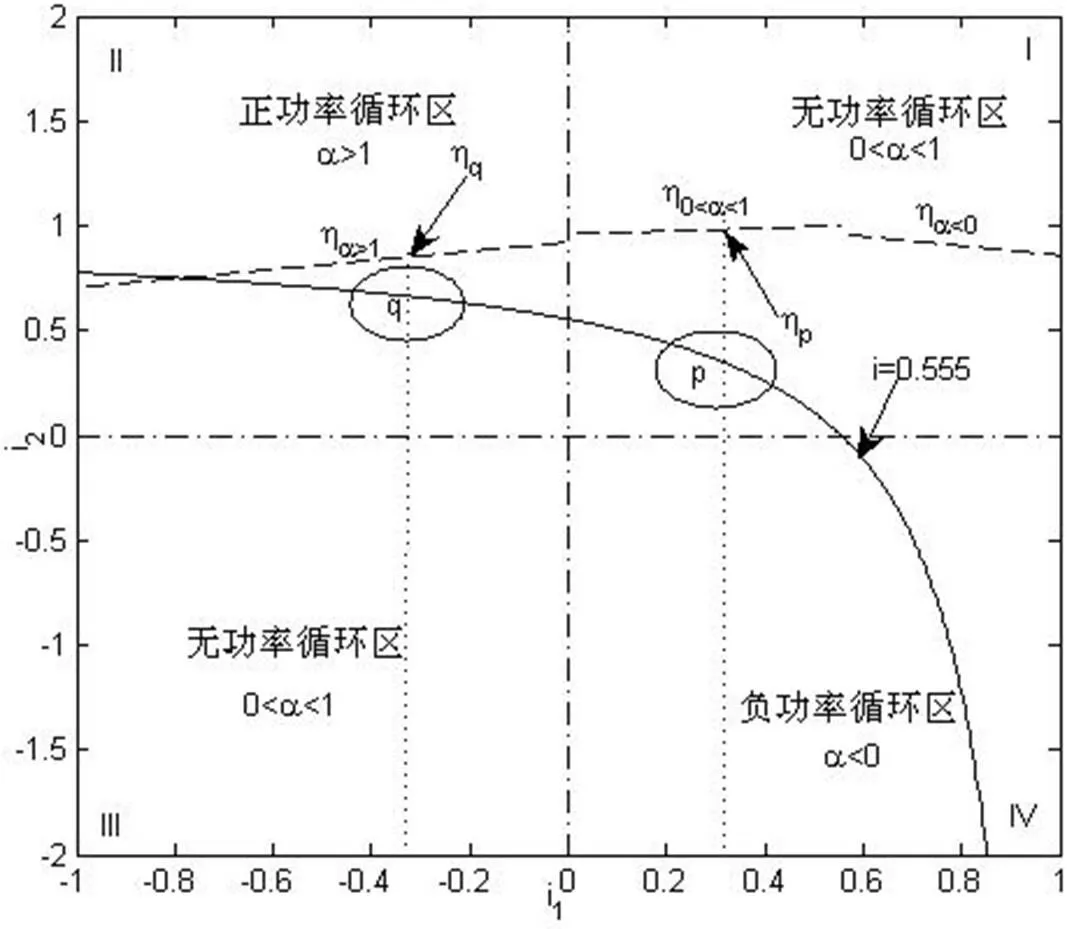
图3 功率分流输入型传动比及效率曲线图

实例图1(3)对应的点为，该点位于正功率循环区，传动效率η=0.849。为获得较高效率的传动，通过调整构件连接和齿轮齿数，即实例图1(4)，得到点，该点位于无功率循环区，对应的传动效率为η=0.976。

通过以上分析，可以看出，当传动比曲线存在正负功率循环的转变区域时，系统传动效率曲线发生急剧变化；当传动比曲线不存在正负功率循环的转变区域时，系统传动效率曲线变化平缓。因此，对于两级封闭行星齿轮传动系统，只有合理地选择单元传动比，才能获得高效率的传动。

7 结论

文中将两级封闭行星齿轮传动系统划分为功率分流输入和功率分流输出两种类型，采用图解分析模型对其内部功率流进行了分析，确定了功率流方向与功率分配系数的关系；通过单元传动比的定义，推导出传动比及功率分配系数与单元传动比的函数关系式，确定了系统内部无功率循环的必要条件，通过给定传动比，以单元传动比1为横坐标，2为纵坐标，绘出一系列传动比及效率函数图像，形成曲线图，通过曲线图可直观地看出循环功率对系统传动效率的影响。

在两级封闭行星齿轮传动系统设计中，应用文中的分析方法可快速地验证传动系统是否存在功率循环，若存在功率循环，则可通过曲线图来选择避免功率循环的单元传动比，然后根据单元传动比合理配置系统中的构件连接和齿轮齿数，获得高效率的传动。

[1] White, G. Derivation of High Efficiency Two-Stage Epicyclic Gears Mech. Mach. Theory, 2003,38:149-159.

[2] Jose M. Castillo. Enumeration of 1-DOF Planetary Gear Train Graphs Based on Functional Constraints. ASME J. Mech. Des., 2002, 124:723-732.

[3] Del Castillo, J. M. The Analytical Expression of the Efficiency of Planetary Gear Trains. Mech. Mach. Theory, 2002, 37(2):197-214.

[4] E.Pennestri, F.Freudenstein. A Systematic Approach to Power-Flow and Static-Force Analysis in Epicyclic Spur-Gear Trains. ASME J. Mech. Des., 1993,115(3):639-644.

[5] David R. Salgado, J. M. Del Castillo. Selection and Design of Planetary Gear Trains Based on Power Flow Maps.ASME J. Mech. Des., 2005, 127:120-134.

[6] 库德里亚夫采夫B.H，Ю.H . 基尔佳舍夫等. 行星齿轮传动手册[M]. 陈启松，张展, 等译. 北京；冶金工业出版社，1986.

[7] E. Pennestri , F. Freudenstein. The Mechanical Efficiency of Epicyclic Gear Trains. ASME J. Mech. Des., 1993,115(3):645-651.

[8] Chia-Pin Liu, Dar-Zen Chen. On the Application of Kinematic Units to the Topological Analysis of Geared Mechanisms. ASME J. Mech. Des., 2001, 123:240-246.

Research on Design of Two-stage Closed Planetary Geared Systems

Duan Fuhai，Zhong yong

(Electromechanical and Automation Engineering Department, Fujian University of Technology, Fuzhou 350108, China)

The relationship between power partition coefficient and power flow in system is studied by analyzing two types of coaxial two-stage closed planetary geared systems. The necessary conditions for non-power circulation are determined. The relationship expression between power partition coefficient and the basic speed ratios is developed. The graphic charts of speed ratios and efficiency are plotted based on practical examples. By analyzing the graphic charts, it shows that the high efficiency transmission can be obtained by properly selecting the basic speed ratios. An effective compact analysis and processing method is presented for design of two-stage closed planetary geared systems.

planetary gear; efficiency; power flow

福建省教育厅项目（JA08166），福建省科技平台建设项目（2008J1002）。