滚动姿态对阳光与卫星向阳面夹角的影响分析
2010-01-08傅伟纯
余 雷 傅伟纯
(北京空间飞行器总体设计部,北京 100094)
1 引言
太阳同步轨道的一个显著特点是:太阳光与卫星轨道面的夹角(即β 角)在一个轨道周期内几乎不变[1-2]。对于三轴稳定对地遥感太阳同步轨道卫星,一般卫星坐标系的+Z 轴是对地, +X 轴为卫星飞行方向,根据右手法则,则卫星Y 轴与轨道面垂直,即卫星Y 面平行于轨道面,因此在一个周期内太阳光与卫星±Y 面夹角保持不变。随着飞行任务的发展,为扩大卫星观测范围,卫星姿态在成像或观测时可能会进行侧摆,即绕卫星滚动轴(+X 轴)在一定角度范围内滚动。此时由于星体姿态的变化,Y 轴不再与轨道面垂直,阳光与向阳面(Y 面)的夹角将发生变化[3-4],导致卫星±Y 和±Z 方向到达的外热流也随之变化,对卫星的温度场分布将造成不同程度的影响,进而对计算分析时高低温工况的选取产生影响。因此有必要针对滚动姿态对卫星外热流的影响及其变化规律进行研究,准确判断全寿命周期内高低温工况[5-7]。图1 为卫星与太阳的位置关系。
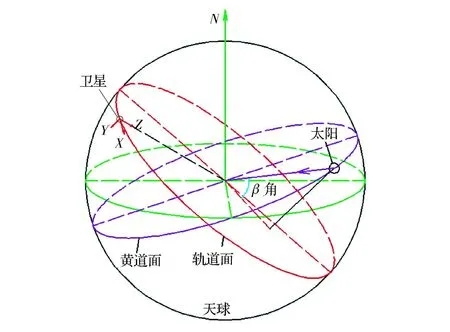
图1 卫星与太阳位置关系Fig.1 Positions of the satellite and the Sun
本文根据太阳同步圆轨道卫星的任务情况,分析了一年中不同时刻、不同滚动角度情况下太阳光与卫星向阳面的夹角变化情况,得出了计算公式,并以某具体型号为例通过了验证。
2 滚动姿态下太阳光与卫星向阳面夹角分析
太阳光与轨道面的夹角[8-9]:
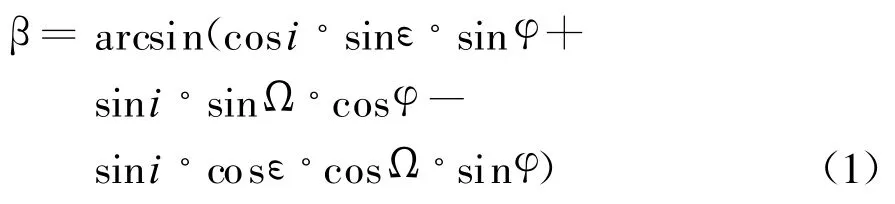
式(1)中:i ——轨道倾角,轨道面法向与赤道面法向的夹角;
ε——天球赤道面与黄道面的夹角;
φ——太阳黄经,黄道面内太阳与春分点的夹角;
Ω——升交点赤经,卫星由南向北通过赤道的点与春分点间的夹角。
根据式(1)可以看出太阳光与轨道面的夹角与4 个参数相关, ε是定值, φ仅与太阳位置有关,与轨道有关的参数仅是i 和Ω。
为便于分析,建立了如图2 所示的天球分析模型。
分析模型图说明:
轨道面——卫星运行所在的平面,此时升交点为点A, 升交点赤经Ω=∠AOV ,轨道面法向为轨道倾角i =∠O′ON 。

图2 分析模型Fig.2 Analysis model
辅助轨道面——卫星在轨道面内以最大赤纬处G 点为起始点运行到点H 时,即θ=∠GOH ,姿态调整为滚动姿态,此时卫星向阳面(-Y 面)将与轨道面成一个夹角,即滚动角ω,卫星向阳面所在的平面将偏离天球中心点,为便于分析, 过天球中心点,作一个辅助轨道面平行于卫星向阳面,此时辅助轨道面的升交点为点B;过O′作一与轨道面平行的平面,该平面与辅助轨道面法向交点为D , 与赤道面法向交点为N, 即辅助轨道面法向为ω=∠O′OD , θ=∠IO′D =∠AOC 。
由于滚动姿态时卫星向阳面与辅助轨道面平行,因此求解太阳光与卫星向阳面夹角即为求解太阳光与辅助轨道面的β′角,亦即求解辅助轨道面的轨 道 倾 角 i′ =∠DON 和 升 交 点 赤 经 Ω′=∠AOV 。
2.1 辅助轨道面倾角i′
根据三角形几何关系可知:

因此
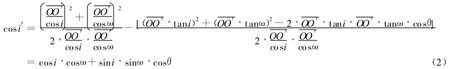
即辅助轨道面的轨道倾角为
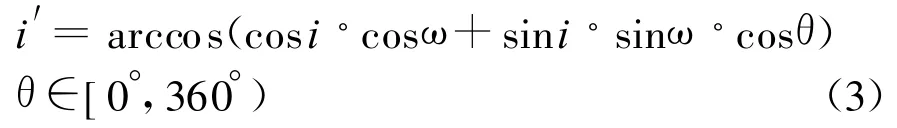
2.2 辅助轨道面升交点赤经Ω′

定义θ′=∠COB ,则

当θ∈[0°,360°)时,式(5)是分段单调变化的,存在两个拐点,即当时所对应的θ1和θ-1值,即

因此
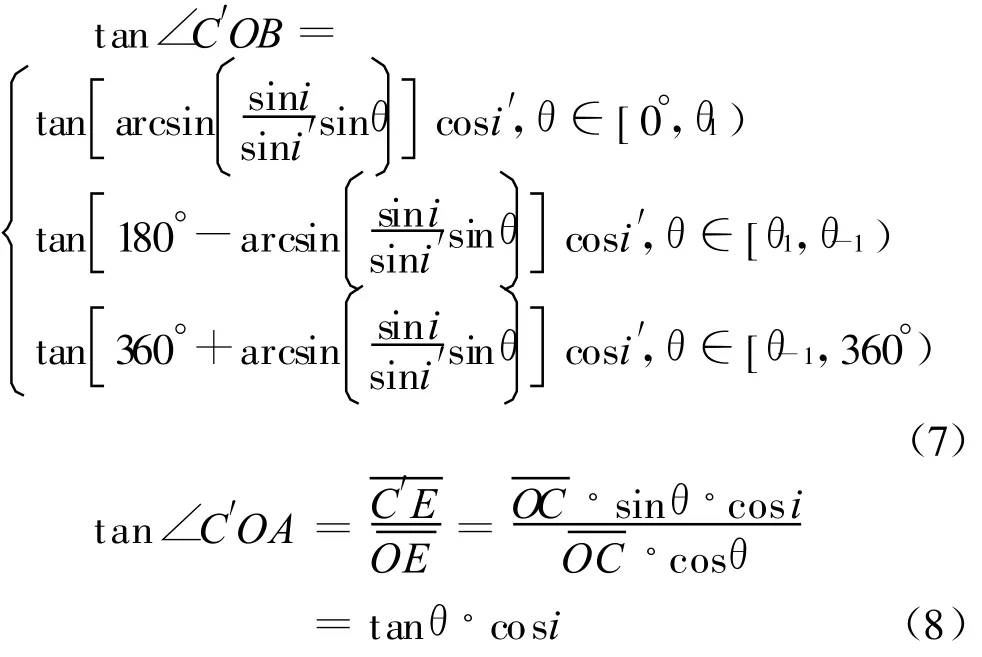
将式(7)和(8)代入式(4)即得[10]

即辅助轨道面的升交点赤经为

2.3 辅助轨道面β′角
根据式(1)、(3)、(6)、(9)可以得到辅助轨道面的β′角,即太阳光与滚动姿态卫星-Y 面的夹角为

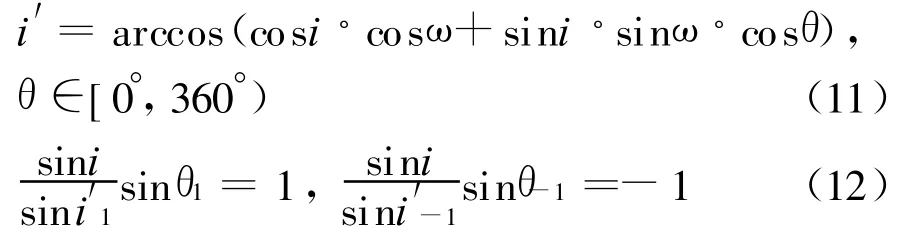
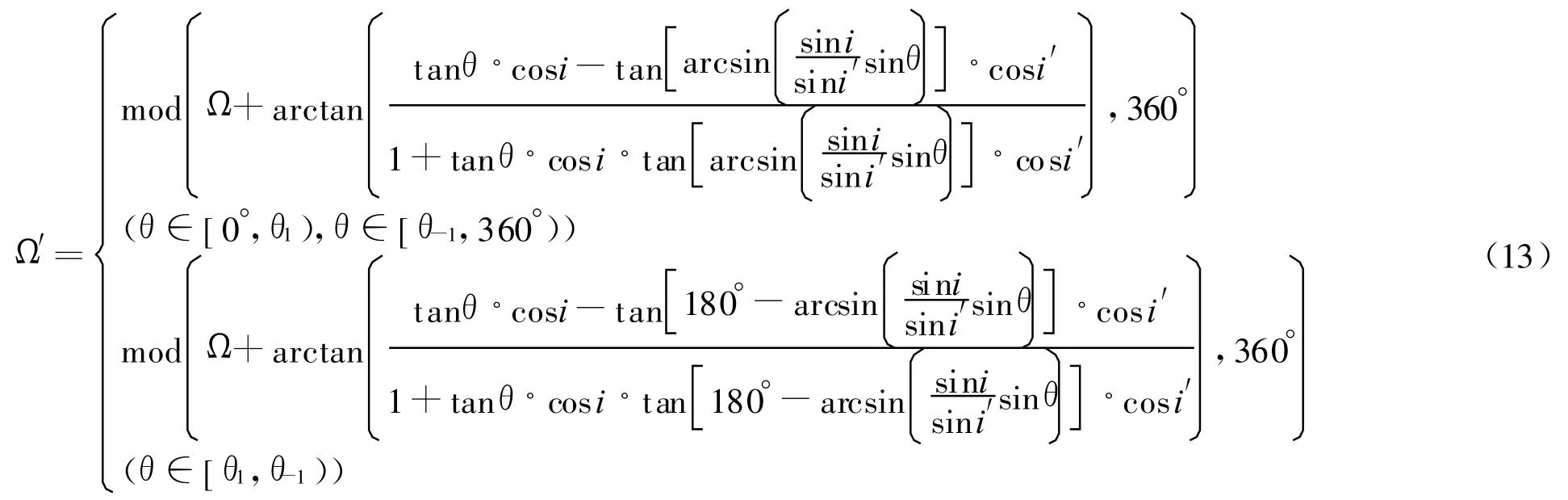
其中:θ——轨道面内从卫星最大赤纬处开始顺卫星运行方向运动的夹角;
ω——卫星滚动角,绕卫星飞行方向(+X 轴)旋转的角度;
i ——轨道倾角,轨道面法向与赤道面法向的夹角;
ε——天球赤道面与黄道面的夹角;
φ——太阳黄经,黄道面内太阳与春分点的夹角;
Ω——升交点赤经,卫星由南向北通过赤道的点与春分点间的夹角。
3 分析结果验证与实例
为验证理论分析结果的正确性,选取某典型太阳同步轨道, 利用常用工程外热流分析软件NEVA DA 计算了侧摆姿态下向阳面的太阳直射外热流,从而反推出卫星向阳面与太阳光的夹角β′。
某太阳同步轨道参数为:
1)太阳同步圆轨道;
2)轨道高度:500 km;
3)轨道倾角:i =97.4°;
4)卫星滚动角范围:ω=±35°;
5)降交点地方时:10 ∶30 am 。
图3 为在该太阳同步轨道下侧摆ω=10°情况下本文理论分析与N EVA DA 数值计算反推结果β′的比较,从图中可看出,理论分析与N EVADA 数值计算反推结果完全一致,从而证明理论推导的正确性。
下面以上述太阳同步轨道为例,按表1 选取几个典型时刻,分析滚动角对辅助轨道面β′角的影响,分析结果如图4~图8 所示。从分析结果可以得出如下结论:
1)卫星姿态绕滚动轴滚动后,阳光与卫星向阳面的夹角将发生周期性变化;
2)在一个轨道周期内,随着滚动角度的增大,阳光与卫星向阳面的夹角变化幅度增大;
3)在一个轨道周期内存在两个特殊的位置,在该处,卫星姿态发生滚动后,阳光与卫星向阳面的夹角不变,即等于β 角;这两个特殊位置随着季节的不同而发生变化;
4)当太阳位于天球南半球,卫星滚动角ω大于0°,卫星运行角θ=0°时,阳光与卫星向阳面的夹角小于β 角;当太阳位于天球北半球,情况正好相反,即当卫星滚动角ω大于0°,卫星运行角θ=0°时,阳光与卫星向阳面的夹角大于β 角。

表1 滚动姿态下β′角Table 1 β′angle in rolling mode
4 结论
本文从理论分析角度研究了滚动姿态对卫星向阳面与太阳光夹角β′的影响,得出了不同滚动角、不同时刻条件下β′的变化规律。并与N EVADA数值计算反推值进行了对比,两者结果完全一致。研究结果对于滚动姿态下卫星外热流分析具有参考意义,对于整星散热面的选取具有现实意义。
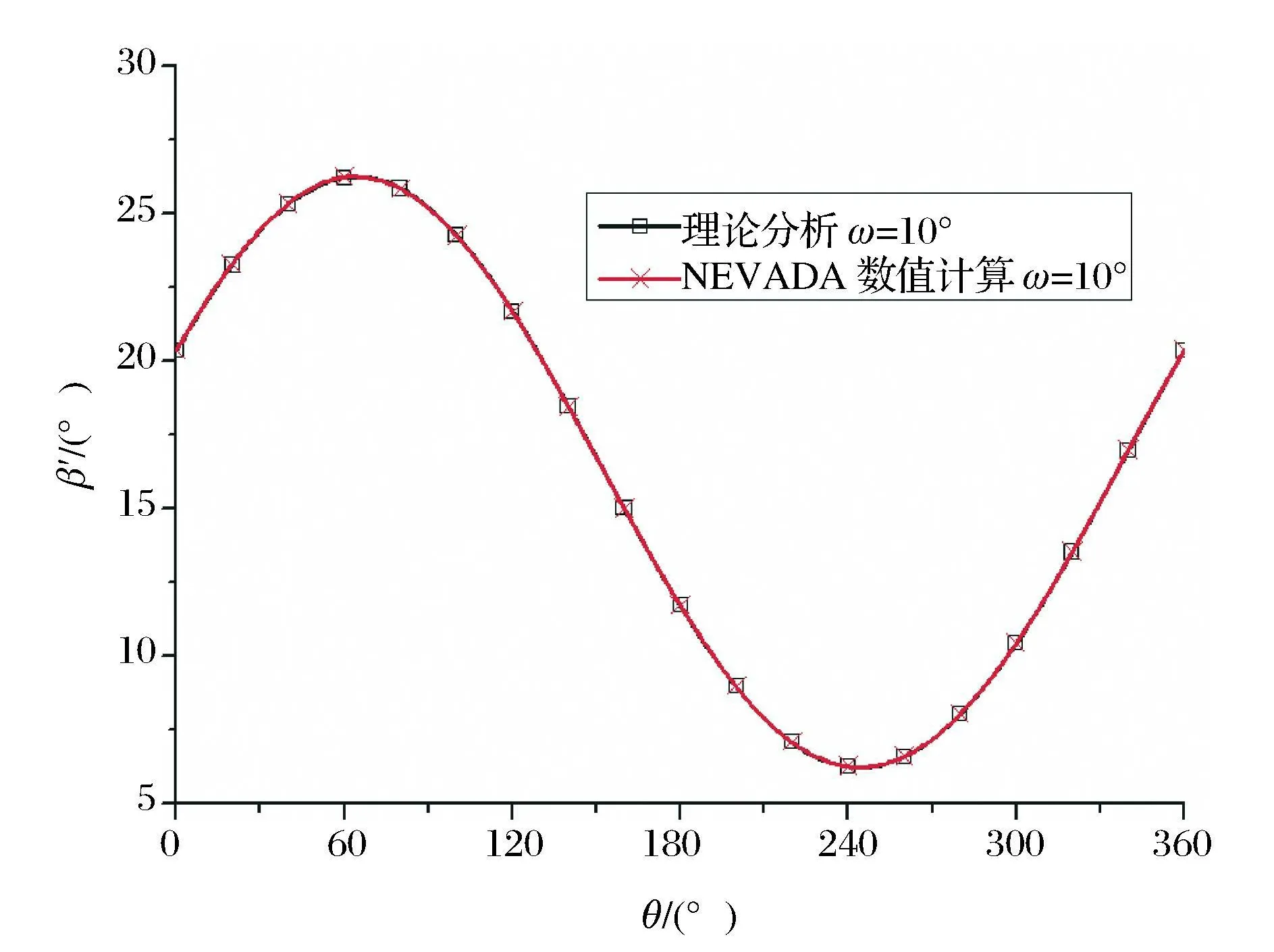
图3 β′角(6月2日)Fig.3 β′angle(2 Jun.)

图4 β′角(1月3日)Fig.4 β′angle(3 Jan.)

图5 β′角(7月6日)Fig.5 β′angle(6 Jul.)

图6 β′角(2月9日)Fig.6 β′angle(9 Feb.)

图7 β′角(6月2日)Fig.7 β′angle(2 Jun.)
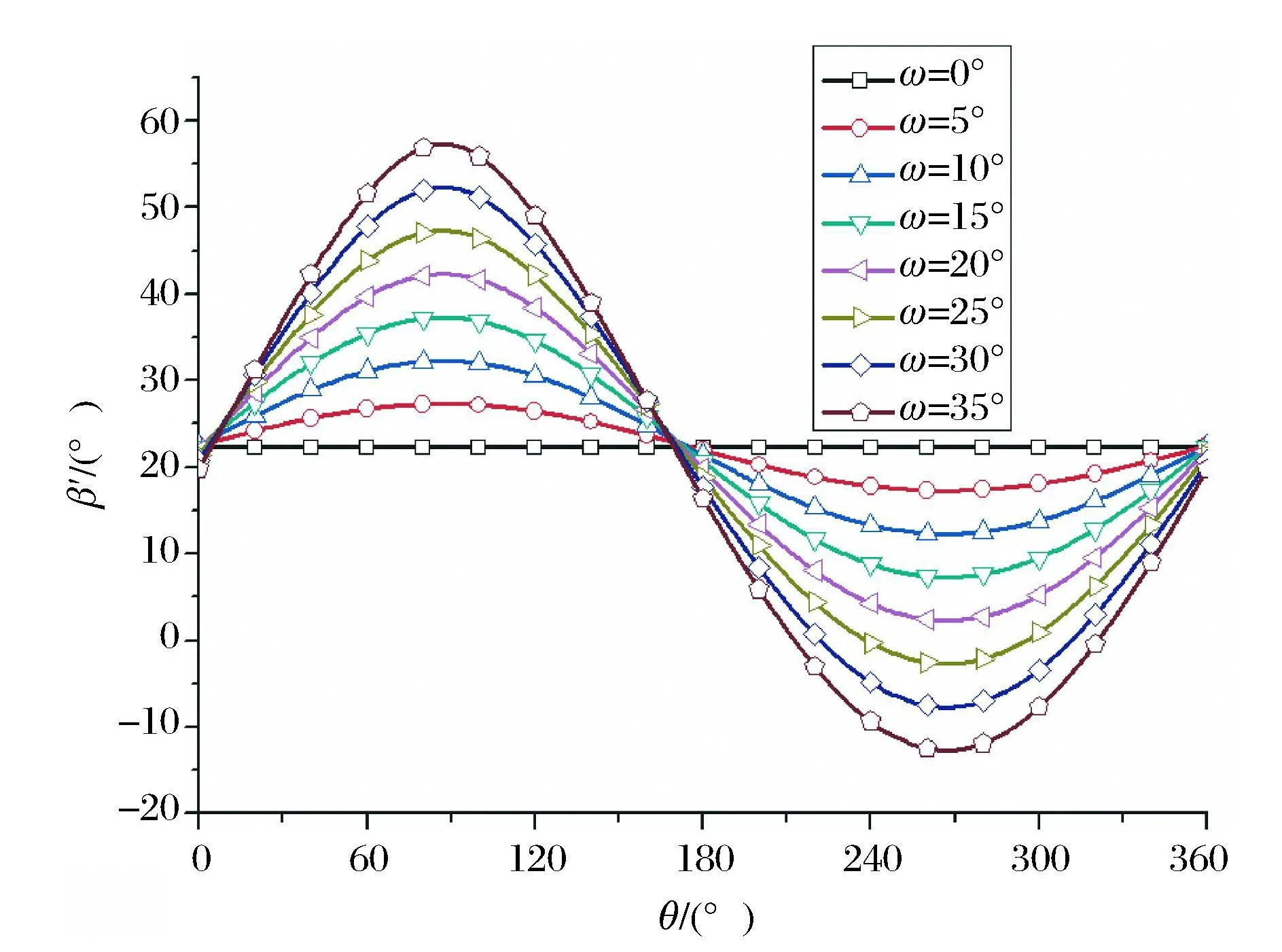
Fig.8 β′角(3月23日)Fig.8 β′angle(23 Mar.)
)
[1]赵欣.卫星热设计中β 角在不同轨道下的变化规律分析[J].航天器工程,2008,17(3):57-61
[2]钟奇, 文耀普,李国强.近地热环境参数对航天器温度影响浅析[[J].航天器工程, 2007,16(3):74-77
[3]江海, 钟奇,刘伟,麻慧涛.大椭圆轨道太阳照射问题研究[C]//江西南昌:第八届空间热物理会议论文集,2007
[4]章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,1998
[5]徐小平,麻慧涛, 范含林.具有强适应性热控技术的概念研究[C]//广西桂林:第六届空间热物理会议文集,2003
[6]Robert D K.Satellite thermal control for systems engineers[M].Virginia:American Institute of Aeronautics and Astronautics, Inc, 1998
[7]Frohlich C, Brusa R W.Solar radiation and its variation in time[J].Solar Phys, 1981(74):209-215
[8]闵桂荣 主编.卫星热控制技术[M].北京:中国宇航出版社, 1991:49-51
[9]Gilmore D G.Spacecraft thermal control handbook[Z].Volume I:Fundamental Technologies, 2ndEdition.The Aerospace Press, EI Segundo, California.2002:40
[10]《数学手册》编写组.数学手册[Z].北京:高等教育出版社, 2002:39
