抛石挤淤机理及其颗粒流数值模拟研究

张明鸣 ，徐卫亚，夏玉斌，周先齐

(1. 河海大学 水利水电工程学院，江苏 南京，210098；2. 河海大学 岩土工程研究所，江苏 南京，210098；3. 中国交通建设集团 水运规划设计院有限公司，北京，100007；4. 厦门理工学院 建筑工程系，福建 厦门，361024)

围海造地具有在不减少现有耕地情况下能使土地面积增大的优点。围海造地的围堤形式通常采用袋装砂或者抛石。如果淤泥较浅时，一般采用抛石(袋装砂)挤淤或者清淤换填袋装砂堤；淤泥较深时，采用爆破挤淤或者排水固结加固淤泥基础袋装砂成堤。本文作者主要研究抛石挤淤深度计算分析方法及其影响因素。对于挤淤深度的计算，杨光煦[1−2]提出了以下卧淤泥极限承载力计算极限挤淤深度的方法；赵简英等[3]在此基础上进行了改进，使公式更加直观；曹阳等[4−7]从压载理论出发结合抛石边坡失稳造成淤泥挤出的原理分析了抛石挤淤地基的挤淤效果。以上方法对于抛石挤淤或者袋装砂挤淤均采用同一算法，没有加以区分。但通过实际检测发现，抛石挤淤深度明显大于袋装砂挤淤深度。为此，本文作者结合大量现场检测数据对压载挤淤计算方法进行改进，并考虑水深的影响。考虑到该方法无法考虑施工控制条件对挤淤深度的影响，引入颗粒流离散元理论(PFC)模拟施工过程及抛填石料散粒体特性，以便得到更符合实际情况的计算挤淤深度的方法，并为常用的施工控制条件提供理论支持。

1 基于压载理论的抛石挤淤深度分析

1.1 压载理论及修正公式

杨光煦[1−2]认为：抛石挤淤是通过压载使下卧软弱土层失稳破坏，使其被挤出，块石下沉，随着深度加大，淤泥层承载力提高，块石与淤泥达到一个平衡态，此即为最终挤淤深度。经赵简英等[3]整理后的承载力公式计算挤淤深度方法为：

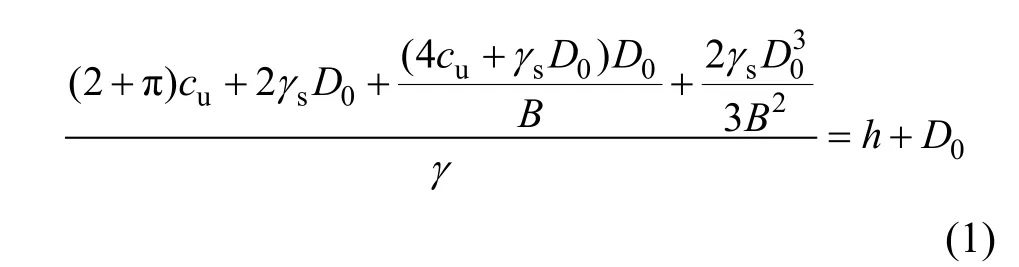
式中：h为堤身原泥面以上高度(m)；D0为堤身自重挤淤下沉量(m)；γs为淤泥重度(kN/m3)；γ为填料重度(kN/m3)；cu为淤泥抗剪强度(kPa)。

1.2 工程实例地质概况

1.2.1 深圳港大铲湾围堤工程

深圳港大铲湾港区位于深圳西部珠江口，覆盖土层主要为第四系全新统近期海相沉积层，含水率较高，均超过70%，强度低，软土层厚度为5～9 m。相关土层主要参数如表1所示。

表1 深圳港大铲湾港区三期工程部分土层参数Table 1 Partial soil layer parameters of tertiary project in Dachan Gulf Region of Shenzhen Haven

1.2.2 海南马村一期工程

海口港马村港区一期工程(后简称马村)位于海口市西部琼州海峡南岸，上覆土层为第四系全新统海相沉积(Q4m)的淤泥及淤泥夹砂层，厚度为0.40～4.40 m，平均厚度为1.93 m。相关地层主要参数如表2所示。

表2 海南马村一期工程相关地层主要参数Table 2 Main parameters of relative layers in 1st project in Macun, Haikou

1.3 计算结果与实测结果比较分析

利用式(1)分别对深圳市大铲湾港区三期造陆工程和海南海口港马村港区一期工程的抛石挤淤深度进行计算，并与实测挤淤深度进行比较，结果如表 3所示。

表3 挤淤深度计算结果与实测平均值Table 3 Calculation result and average depth of measurement of Squeeze out ooze depth

挤淤深度实测结果分别取两堤肩及堤心位置钻孔检测挤淤深度的平均值。由表3可见：挤淤深度计算结果与实际钻探结果相差较大，计算值普遍偏小。挤淤深度计算值与实测值存在较大差异的主要原因主要有：

(1) 抛石具有的动能破坏土骨架，能够使石块进入土层。

(2) 石块为散粒体结构，在局部形成较大压载，刺入淤泥颗粒中。

(3) 施工控制因素使挤淤深度存在差异。

(4) 压载法无法考虑块石直径对挤淤效果的影响。

由极限地基承载力基础发展而来的压载挤淤公式无法体现上述因素的影响。因此，为了更准确地研究抛石挤淤深度，需要引入其他算法。该算法应能够模拟抛石作为散粒体材料以一定速率进入淤泥及局部荷载集中的特性。

2 颗粒流离散元分析方法及其在抛石挤淤工程中的应用

由于模拟抛石挤淤问题存在网格侵入，有限元法难以解决此问题。因此，本文作者采用Cundall等[8−9]提出的颗粒流理论将抛石等效为独立颗粒体，模拟分析大铲湾三期陆域形成工程抛石挤淤成堤的施工过程。

2.1 颗粒离散单元法及PFC2D软件简介

颗粒离散元法是把颗粒材料的力学响应问题从物理域映射到数学域而进行数值求解的方法。与此相对应，物理域内真实的散粒介质微粒(Grains)被数学域内抽象的颗粒单元(Particles)所代表，通过对试样颗粒单元几何形状的设计、相互作用接触类型的选择、试样边界条件和初始条件的确定、试样若干应力平衡状态的迭代分析等，实现对材料受力变形特征的数值模拟。

PFC2D是由Cundall等[8]发明的颗粒流离散元计算软件，它将材料假定为刚体颗粒，允许刚体颗粒可以少量重叠，刚体圆球之间的连接主要表现为法向和切向刚度及抗拉和抗剪强度等参数指标，颗粒之间运动遵循牛顿第二定律。

本文借鉴张翠兵等[9−10]的思路，也利用PFC的刚体圆盘来模拟抛石石块。提出刚体球从高处滚落时将势能转化为动能，同时，少数先进入土体的刚体球可以模拟局部加载较大刺入淤泥的状况。以更细小的颗粒模拟淤泥结构，并通过颗粒的相互接触模拟淤泥宏观强度指标。由于抛石挤淤主要作用时间较短，故淤泥本身的固结在本次模拟中不予考虑，因而，在将细观参数与宏观参数对应拟合时，只考虑强度指标。

2.2 淤泥颗粒细观参数选取

颗粒流的细观模拟原则是通过改变颗粒单元机器集合体的细观力学性质，使之逼近材料的宏观力学参数。采用数值模拟试验对实际材料进行模拟，需要不断调整数值试验的输入参数，使数值模拟结果与物理试验结果相吻合。

针对大铲湾三期陆域形成围堤工程中的淤泥材料进行数值模拟试验，分别进行了无侧限及围压为0.5，1，2和5 kPa的双轴试验。通过不断调整颗粒间的黏结强度及摩擦因数，获得与宏观强度响应的近似淤泥强度曲线(见图1，其中，c为剪切力，φ为内摩擦角)，此时，微观参数法向刚度、切向刚度均取为4 kPa，方差为200 Pa，摩擦因数取为0.5。模拟结果如图1所示。模拟结果与大铲湾工程中流泥与淤泥各宏观参数的平均值较接近。

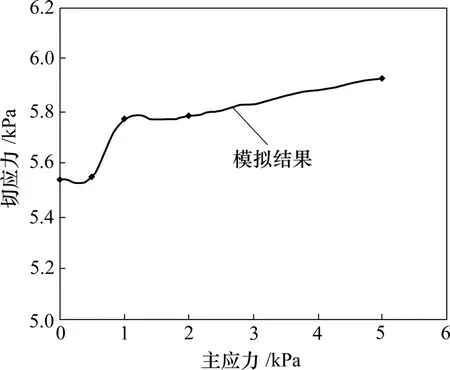
图1 淤泥强度曲线Fig.1 Strength curve of ooze

2.3 模型的建立及计算工况

2.3.1 模型的建立

在计算过程中，首先需要对淤泥材料进行模拟。根据地勘报告，淤泥材料平均孔隙比约为2.0，单个圆盘型颗粒作为基本单元组成的颗粒集合不可能达到该孔隙比，考虑采用CLUMP簇单元模拟淤泥材料，材料微观参数选用数值模拟试验获得。

本文共建立2个模型：一个是据实际典型断面(如图2所示)土层分布建立计算模型；另一个是假定淤泥厚度为15 m，以分析淤泥厚度对挤淤的影响。以PFC提供的WALL结构模拟已有陆域，抛石从已有陆域滚落进入淤泥层。

2.3.2 计算工况

(1) 第 1组工况。为了分析抛填强度对挤淤的影响，分别对上述2个模型计算2次、4次、8次抛填完成1个断面工程量工况的挤淤深度，以分析抛石强度和淤泥层厚度对挤淤深度的影响。完成1个断面需要的次数越少，意味着抛填速度越快，堤头堆载越高。抛石体圆盘直径为 30～50 cm，与施工中采用 100 kg块石的直径较接近。

(2) 第2组工况。采用淤泥厚度为15 m的模型分别分析抛石直径分别为20～30，30～50和50～80 cm分4次抛填的挤淤情况，以分析石块直径对挤淤深度的影响。

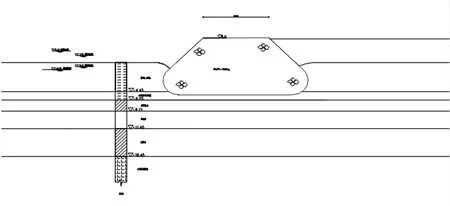
图2 实际典型断面Fig.2 Practical typical section

2.4 模拟结果分析

2.4.1 抛石强度对挤淤深度的影响

经分析，PFC第1组工况计算结果如图3、图4及表4所示。若按照不同的抛填强度施工，则挤淤深度不一样，一次性抛填越多，抛填施工速度越快，挤淤深度越深，且底面高程更平均，此点与史力生[11]关于阳江核电站抛石挤淤陆域形成工程中现场观测结果相吻合。典型断面颗粒流模拟结果(挤淤深度为抛石颗粒底面的平均深度)与实测结果较吻合。

2.4.2 淤泥层厚度对挤淤深度的影响

按照实际土层厚度模拟挤淤结果，抛石下方存在厚度约为1 m的淤泥层，与实际钻孔检测结果相吻合。若采用15 m厚淤泥模型，则相同抛填强度下挤淤深度可达8 m以上，大于实际深度，说明边界约束影响挤淤深度，此现象与文献[2, 12]中提到的“挤淤深度与抛填速度及挤淤不可能完全挤走，总有淤泥残余”的论点吻合。林本义等[13−14]认为蛇口填海工程中挤淤深度达到10 m左右。而蛇口港区与大铲湾港区隔海相望，地质条件相近，只是淤泥深度更深。蛇口填海工程中的实测结果与15 m厚淤泥模型的计算结果相吻合，结合大铲湾港区挤淤模拟结果可得到：挤淤深度越大，块石层下残余淤泥便越厚。

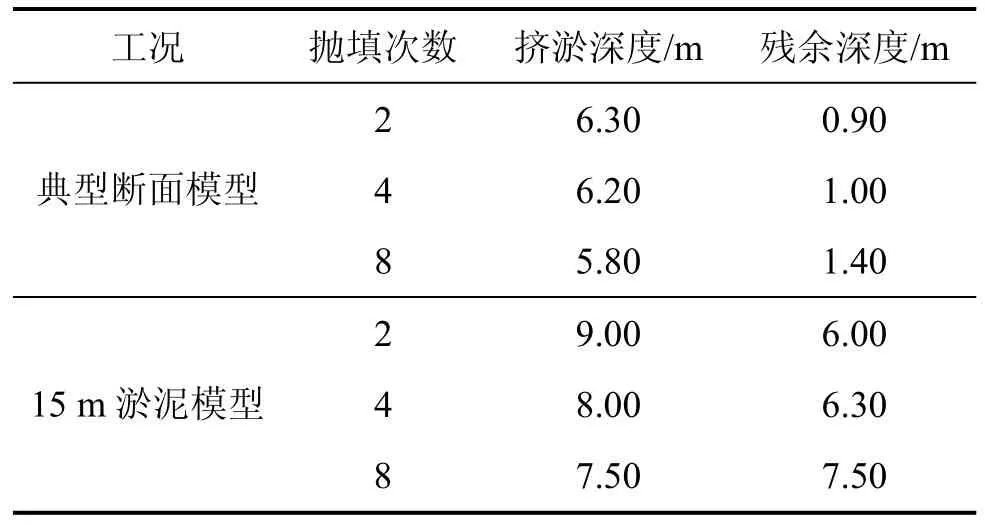
表4 不同抛填次数时的挤淤深度Table 4 Simulating results of different processes

图3 下卧淤泥贝壳混合层工况下不同抛填强度计算结果Fig.3 Calculation results of backfilling rock for subjacent mixture of ooze and oyster shell

2.4.3 抛石直径对挤淤深度的影响

不同直径的抛石挤淤深度结果如图 4(b)、图 5、图6及表5所示。可见：抛石直径越大，挤淤深度越大。这主要是由于直径越大的抛石下落时受到周围颗粒的约束越少，越容易形成局部荷载集中，造成挤淤深度加大。通过记录第1次抛填的块石的位移随时间变化的关系如图7所示。由图7可见：大部分抛石挤淤变形都发生在第1次抛填过程中，后续抛填使底层块石沉降不断增加，但增加幅度较小。图8所示为不同直径石块与最终挤淤深度关系曲线，将其线性拟合(见式(2))可以得到：当块石直径逼近0 cm时，抛砂或抛土挤淤时挤淤深度为4.6 m，与由式(1)所得的计算值接近。由此可以得到：如果不考虑抛石动能及局部荷载集中的影响，则在抛砂、袋装砂挤淤计算中压载理论是适用的，同时，此结果也从另一个侧面证明PFC模拟结果较准确。

图4 不同抛填强度计算结果(淤泥层厚度15 m工况)Fig.4 Calculation results of backfilling for subjacent ooze of 15 m depth

表5 不同直径的抛石挤淤深度Table 5 Simulating depths of different rock sizes

图5 抛填块石直径为20～30 cm抛填强度计算结果Fig.5 Result of backfilling rocks with 20−30 cm diameter

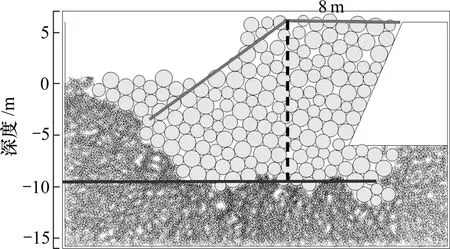
图6 抛填块石直径为50～80 cm抛填强度计算结果Fig.6 Result of backfilling rocks with 50−80 cm diameter

图7 底层块石沉降曲线Fig.7 Curves of settlement of rocks at bottom

图8 挤淤深度与块石直径的关系Fig.8 Relationship between depth of squeeze out ooze and size of rock

挤淤深度与块石直径的线性拟合函数表达式为：

式中：h为挤淤深度；dmax为抛填块石的最大直径。

3 结论

(1) 抛石能够挤淤不仅是压载引起的，而且是抛石体从高处以势能转化的动能进入淤泥体，破坏淤泥结构，局部应力集中造成块石挤开淤泥进入其中引起的。

(2) 颗粒流算法可以较好地模拟抛石挤淤施工过程，计算结果与现场实测结果较吻合。

(3) 抛石挤淤不能完全将淤泥挤出，抛石层下都存在一定泥石混合层。

(4) 一次性抛填较多的石料和连续抛填可加大挤淤深度。

(5) 抛填时采用的块石直径越大，则挤淤深度越大。

(6) 抛填挤淤造成的块石下沉大部发生在第 1次抛填后。

(7) 为了保证抛石堤落底，在抛石围堤设计时要求超高连续抛填，使每次抛填量大，同时，在条件允许和级配合理的情况下，抛填石料直径应尽量大。

[1] 杨光煦. 挤淤[J]. 水利学报, 1992(5): 59−64.YANG Guang-xu. Squeeze out ooze[J]. Journal of Hydraulic Engineering, 1992(5): 59−64.

[2] 杨光煦. 压载挤淤研究[J]. 岩土工程学报, 1992, 14(2): 72−76.YANG Guang-xu. Research on loading squeeze-out ooze[J].Chinese Journal of Geotechnical Engineering, 1992, 14(2):72−76.

[3] 赵简英, 王健, 吴京平. 控制加载爆炸挤淤置换法在工程中应用[J]. 岩土力学, 2006, 27(2): 332−335.ZHAO Jian-ying, WANG Jian, WU Jing-ping. An application of blast method to squeeze mud and replacement with controlled loading[J]. Rock and Soil Mechanics, 2006, 27(2): 332−335.

[4] 曹阳, 颜荣贵, 王广华, 等. 厚层淤泥超载挤淤法建基对策及工程实例[J]. 岩石力学与工程报, 2002, 21(11): 1676−1680.CAO Yang, YAN Rong-gui, WANG Guang-hua. Case study on counter-measure of foundation on thick muck by method of overloading and removing slit[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(11): 1676−1680.

[5] 汪茂冬. 强夯抛填定向挤淤在地基处理中的应用[J]. 工程设计与建设, 2004, 36(5): 26−28.WANG Mao-dong. Application of oriented removing of silt with filling and dynamic compaction in foundation treatment[J].Engineering Design and Construction, 2004, 36(5): 26−28.

[6] 赵渭军, 严盛, 宣伟丽, 等. 涌潮河口桩式丁坝的护滩保塘效果分析[J]. 水利学报, 2006, 37(6): 699−703.ZHAO Wei-jun, YAN Sheng, XUAN Wei-li, et al. Effect of sheet-pile groins on protecting dykes and flats in tidal bore estuary[J]. Shuili Xuebao, 2006, 37(6): 699−703.

[7] 余开彪, 王宗国, 张成顺. 强夯置换技术处理公路软土地基试验研究[J]. 岩土力学, 2006, 27(增刊): 969−972.YU Kai-biao, WANG Zong-guo, ZHANG Cheng-shun. Study on dynamic consolidation method for reinforcing soft foundations of highways[J]. Rock and Soil Mechanics, 2006, 27(Suppl):969−972.

[8] Cundall P A, Hart R. Formulation of a three-dimensional distinct element model[J]. Int J Rock Mech Min Sci & Geomech, 1988,25(3): 117−128.

[9] 张翠兵, 邓志勇, 高凌天. 抛石散体振动密实过程的离散元数值模拟[J]. 岩石力学与工程学报, 2004, 23(1): 95−100.ZHANG Cui-bing, DENG Zhi-yong, GAO Ling-tian, et al.Numerical simulation of vibration compacting process on loose media by distinct element method[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(1): 95−100.

[10] 张昭. 砂土中桩基础沉降机理宏细观研究[D]. 上海: 同济大学土木工程学院, 2007.ZHANG Zhao. Macro-scale and meso-scale study of settlement mechanism of pile foundations in sand[D]. Shanghai: College of Civil Engineering, Tongji University, 2007.

[11] 史力生. 推填挤淤工程实践[J]. 中国水利水电科学院学报,2008(3): 9−12.SHI Li-sheng. Backfilling rocks to squeeze out silt in sea beach[J]. Journal of China Institute of Water Resources and Hydropower Research, 2008(3): 9−12.

[12] 徐学勇, 汪稔, 孟庆山, 等. 深厚淤泥爆破挤淤震动效应测试与控制技术[J]. 岩土力学, 2008, 29(12): 3256−3260.XU Xue-yong, WANG Ren, MENG Qing-shan, et al. Monitoring and controlling technology for vibration effect due to deep and thick silt by blasting compaction[J]. Rock and Soil Mechanics,2008, 29(12): 3256−3260.

[13] 林本义. 挤淤填海造地的几个工程问题[J]. 水运工程,1989(3): 39−42.LIN Ben-yi. Some engineering problems of backfilling rocks to squeeze-out ooze[J]. Port & Waterway Engineering, 1989(3):39−42.

[14] 伍荣官. 填土(石)挤淤效果分析[J]. 水运工程, 1990(12):36−38.WU Rong-guan. Effect analysis of backfilling rocks to squeeze-out ooze[J]. Port & Waterway Engineering, 1990(12):36−38.