基于马尔科夫模型的词汇语义相似度计算
2010-01-05皮慧娟
皮慧娟
(华侨大学 计算机科学与技术学院,福建 泉州 362021)
基于马尔科夫模型的词汇语义相似度计算
皮慧娟
(华侨大学 计算机科学与技术学院,福建 泉州 362021)
在《知网2002》的基础上,充分利用其层次结构,引入了马尔科夫模型来计算词汇语义相似度,实验证明,算法取得较理想的实验结果·
词汇语义相似度;知网;马尔科夫模型
词汇语义相似度有两类常见的计算方法,一种是根据某种世界知识或分类体系来计算[1-3],另一种利用大规模的语料库进行统计[4-6]·
根据世界知识或分类体系计算词语语义距离的方法,一般是利用将所有的词组织在一棵或几棵树状的层次结构中的同义词词典·在一棵树状图中,任何两个节点之间有且只有一条路径,于是,这条路径的长度就可以作为这两个概念的语义距离的一种度量·王斌采用这种方法利用《同义词词林》来计算汉语词语之间的相似度[1]·有些研究者考虑的情况更复杂·Agirre和Rigau在利用WordNet计算词语的语义相似度时,除了节点间的路径长度外,还考虑了其他一些因素·如:概念层次树的深度、高度等[7]·另一种词汇语义相似度的计算方法是用大规模的语料来统计·这里不再详述·
1 研究背景
1.1 马尔科夫模型
(1)马尔科夫特性:若在某随机过程{X(t),t∈T}在某时刻tk所处的状态已知的条件下,过程在时刻t(t>tk)处的状态只会与过程在tk时刻的状态有关,而与过程在tk以前所处的状态无关·这种特性称为马尔科夫特性,亦称之为无后效性·
(2)马尔科夫过程:设{X(t),t∈T}为一随机过程,E为其状态空间·若对任意的时间t1<t2< …<tn<t,任意的x1,x2,…,xn,x∈E·随机变量X(t)在已知条件:X(t1)=x1,X(t2)=x2,…,X(tn)=xn下的条件分布函数,若只与X(tn)=xn有关而与X(tn-1)=xn-1,…,X(t2)=x2,X(t1)=x1无关,即条件分布函数满足等式:
F(X,t|Xn,Xn-1,…,X2,X1,tn,tn-1,…,
t2,t1)=F(x,t|xn,tn)·(1)则称此过程为马尔科夫过程[8]·
1.2 知 网
《知网》里的核心术语主要有:
概念:对词汇的描述,一个词可以表达为多个概念·
义原:用来描述“概念”的最小单位·
《知网2002》知识库包括:中英双语知识词典;义原分类源文件;知网管理工具;知网说明文件(包括词类表和标识符号说明)等·
本文主要用到词典和义原分类文件:
(1)知识词典的记录样式:中英双语知识词典中每个词语用一条或多条记录来表示,记录样式如下所示:
NO.=037070
W-C=关节
G-C=N
E-C=重要~
W-E=key links
G-E=N
E-E=
DEF={part|部件:PartPosition={heart|心},whole={entity|实体}}
其中,NO.是概念编号,W-C、G-C、E-C分别是汉语词语、词性和例子·W-E、G-E和E-E分别表示英语的词语、词性和例子·DEF表示的是概念的定义,表达了主要的信息·DEF可看成一个树状的结构,如图1所示·其中包含义原:部件、心、实体;还有关系义原:PartPosition,whole·

图1 “关节”的义原关系示意图
(2)《义原分类源文件》说明知网词库中的每个词语由DEF来描述其概念定义,DEF的值由若干个义原及它们与主干词之间的语义关系描述组成·义原(semese)是知网中最基本的、不易于再分割的意义的最小单位·知网通过对约6 000个汉字进行考察和分析来抽取·对1 500多个义原总结了上下位、同义、反义、对义、属性-宿主、部分-整体、材料-成品、事件-角色等若干种义原间的语义关系·可以看出义原组成的是一个很复杂的网状体系结构,而不是树状结构·不过义原关系中最重要的还是上下位关系,根据义原的上下位关系,所有的“基本义原”组成了一个义原层次体系,这个体系是一个树状结构,这也是进行语义相似度计算的基础[9]·
2 基于《知网》和马尔科夫过程的词汇语义相似度计算
2.1 词汇语义相似度计算和义原相似度的计算
考虑汉语词语W1和W2,如果W1有n个概念:w11,…,w1n;W2有m个概念:w21,…,w2m·规定W1和W2的相似度是各个概念之间的相似度的最大值:

这样词语相似度归结到了概念相似度·
义原相似度的计算一般依据义原的层次体系(上下位关系)来计算,这种基于树状层次结构计算语义相似度的研究已经十分成熟·本文采用基于义原之间路径长度的计算方法·假设两个义原的距离为d,则定义:
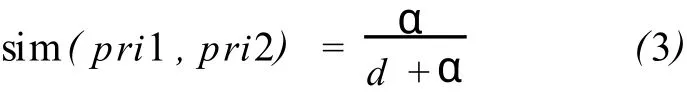
其中,pri1和pri2表示两个义原,d为义原在义原层次体系中的路径长度,α是可调参数·在《知网》系统中义原除了上下位关系还有很多其他关系,本文只讨论上下位关系·
2.2 利用马尔科夫模型计算树状结构的义原体系相似度
2.2.1 关系义原的计算
词语的DEF的义原分为两大类:基本义原和关系义原·笔者认为只有在关系义原相同的条件下才去计算关系义原下的子义原之间的相似度,如果关系义原不同则认为两个关系义原相似度为0·
2.2.2 引入马尔科夫模型的树状义原体系相似度的计算
由1.2中的介绍可知,知网中对词语的定义可看成树状结构,下面先通过对这些树状结构进行分析,从某种程度上分析引入马尔科夫模型来计算词义相似度的合理性;然后提出了义原树之间的相似度求解算法·
(1)树状结构的分析
这是整个工作的核心部分,从前面的分析可以看到词语的DEF是按照义原树的形式表示的,选取“DEF={part|部件:PartPosition={heart|心},whole={entity|实体}}”和“DEF={human|人:Hostof={occupation|职位},domain={education|教育}}”为例,并将后一个序列转换为义原树,如图2所示·

图2 “人”义原树图
如何计算两个义原树的相似度是一个难点,也是整个工作的核心部分·在这里引入一阶马尔科夫模型的方法·
将整个树看作一个序列{x1,…,xn},将义原看成序列中的一个状态,如“部件”就为树1这个序列的最后一个状态;将它的所有子义原作为它的前一个状态·这样义原树形成一个“倒的”状态序列·在图1中:“部件”的前个状态是{“whole”,“PartPosition”},{“whole”,“PartPosition”}的前个状态是{“实体”,“心”}·根据一阶马尔科夫过程,一个状态只和它前一个状态有关而与其他状态无关,那么“部件”只和它的子义原有关而与子义原的子义原无关·这样就将多层的树简化成多个两层的子树了·
由于“人”和“职位”的关系由关系义原“Hostof”相关联,而直接关系不大,所以利用马尔科夫过程来计算是有科学根据的·
(2)义原树的求解过程:
引入一阶马尔科夫模型后,假定一个义原只由它的子节点决定并且和子节点的下层节点无关·然后按照树来递归计算义原树的相似度sim1·这样义原相似度可以定义为两部分:两个节点义原之间的相似度和它们子节点之间的相似度·
如图1和图2所示,两义原树的相似度由“部件”和“人”的相似度和它们的子义原之间的相似度的平均值相加而成·而子义原之间的相似度又是由子义原本身的相似度和子义原的子义原之间的相似度决定,由递归计算可以得到整棵树的相似度·步骤如下:
①计算父节点之间的相似度,这直接化成了义原相似度的计算(公式(3))·在此例中先计算“部件”和“人”的相似度s1·由于是第一义原,可以赋一个比较高的权重m·
②计算两个父节点的子节点之间的相似度,并求其平均相似度s2,可以赋相对低的权重n·但应该遵循m+n=1·最后sim1=m*s1+n*s2·在这个例子中:计算“部件”的子节点(whole,PartPosition)和“人”的子节点(Hostof,domain)之间的相似度·由于子节点都是关系义原而且各不相同,根据上面关系义原相似度的定义·在这里可以认为子节点的相似度为0·
③递归计算s2,由于词语的义原树深度一般不超过4,所以计算复杂度并不大·
3 实验结果及评价
3.1 参数的设定
本文认为两个词之间是否相似,主义原的比重比较大,其他义原的比重按照义原树的层次依次减小,本着此原则,根据多次实验和调整,将参数设置如下:
(1)α=1.6·
(2)如果两个义原存在于不同的义原文件,那么义原的相似度应该是一个比较低的值,设定这两个义原的相似度为0.04·
(3)如果词语是上下位关系,那么它们的相似度会比较高,设定相似度为0.611 1·
(4)在计算树状结构义原中,由于m>n,且m+n=1,设定m=0.6,n=0.4·
3.2 实验结果和比较
根据以上方法,本文实现了一个程序模块·并将计算结果和文献[2]中的算法比较,结果如表1所示·
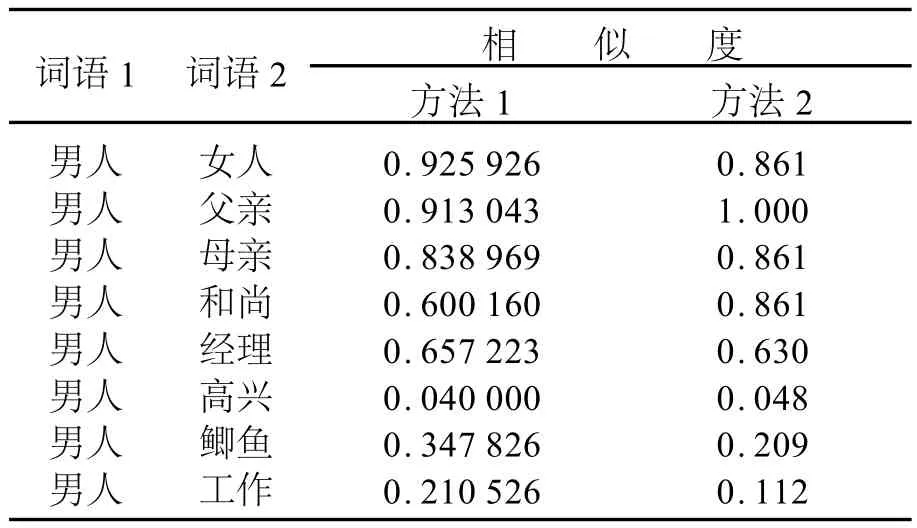
表1 两种方法词义相似度的比较
从表1可以看出本文的算法取得了比较好的结果,而且在某种程度上更科学:如“男人”和“父亲”在方法2的算法中相似度为1,这显然不是很合理的;而“男人”和“女人”的相似度和“男人”和“母亲”的相似度一样,这也是不合理的·本文认为“男人”和“女人”都是一种对人的概述而且形式也一样,所以“男人”和“女人”的相似度应该更高;在方法2的结果中相对于“男人”和“经理”,“男人”和“和尚”的相似度过高,这也是不合理的·“男人”和“鲫鱼”的相似度比“男人”和“工作”高,这和方法2的结果接近·
4 结 论
《知网》采用了1 500多个义原,通过一种描述知识来对每个概念进行刻画·每个词有多个概念,本文计算两个词的概念之间的相似度,并求最大值为词汇语义相似度,从而将词语相似度转化为求概念相似度;为了计算树状结构义原的相似度,借鉴了一阶马尔科夫模型的思想并进行递归计算:每个义原的计算只依赖自己和自己的子节点,和其他的节点不相关·从而将概念相似度转化为义原相似度的计算;最后通过义原的上下位语义距离来求义原的相似度·本文只用到了义原的上下位关系而略去了其他关系,在未来的工作中将加上其他关系使得结果更加精确·
[1] 王斌·汉英双语语料库自动对齐研究[D]·北京:中国科学院计算技术研究所,1999·
[2] 刘群,李素建·基于《知网》的词汇语义相似度的计算[C]∥第三届汉语词汇语义学研讨会论文集·台北,2002·
[3] 李涓子·汉语词义排歧方法研究[D]·北京:清华大学,1999·
[4] 鲁松·自然语言中词相关性知识无导获取和均衡分类器的构建[D]·北京:中国科学院计算技术研究所,2001·
[5] Dagan I,Marcus S,Markovitch S.Contextual word similarity and wstimation from sparse data[C]∥Proceedings of the 31st AnnualMeeting of the Association for Computational Linguistics(ACL).Ohio State University,1993:164-171.
[6] Dagan I,Lee L,Pereira F.Similarity-based models of word cooccurrence probabilities[J].Machine Learning,Special issue on Machine Learning and Natural Language,1999,34(1/2/3):43-69.
[7] Agirre E,Rigau G.A proposal for word sense disambiguation using conceptualdistance[C]∥Proc.ofInternational Conference Recent Advances in Natural Language Processing(RANLP).Tzigov Chark,Bulgaria,1995:258-264.
[8] Rabiner L R.A tutorial on hidden Markov Models and selected applications in speech recognition[C]∥Proceedings of the IEEE,1989,77(2):257-286.
[9] 董振东·知网中文版[EB/OL]·[2009-07-16]http:∥www.keenage.com/html/c-index.html.
Word Similarity Computing Based on Markov Model
PI Huijuan
(College of Computer Science and Technology,Huaqiao University,Quanzhou 362021,China)
Markov Model was applied to compute the meaning similarity of words,on the basis of HowNet 2002.Experiments showed that the algorithm achieved satisfactory results.
word similarity;HowNet;Markov Model
TP 391
A
1008-9225(2010)01-0005-04
2009-09-21
皮慧娟(1971-),女,湖北鄂州人,华侨大学实验师,硕士·
【责任编辑 李 艳】
