发现特殊值 渗透极限思想
2010-01-04方爱斌
方爱斌
“鸡兔同笼”问题作为人教版六年级上册第七单元“数学广角”中的教学内容,教材中先后呈现了列表法、假设法、方程法、抬足法四种不同的解决问题的策略。此问题蕴含着丰富的数学思想方法,适合于小学低中高各年段,每个年段都有不同的侧重方法,与学生的发展思维相适。以“鸡兔同笼”为教学素材,苏教版作为替换策略的练习题,北师大版把课题定位为《尝试与猜测》,而人教版则体现多种策略解决问题。作为“通性通法”的尝试列表法解题策略,在六年级人教版多种策略中如何定位?反复思考之后,我以为,通过引导学生发现特殊值,渗透极限逼近思想,把猜测变成确定的规律,将尝试列表法进行优化,有其独特的教育价值。
教学片断:
例:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”以史激趣,导入新课后,题目化简为:“笼子里有若干只鸡和兔,从上面数,有 8个头,从下面数,有26只脚。鸡和兔各有几只?”
学生尝试猜测,探索规律。
1.任意猜:(交流后,汇报你是怎么猜的,以及猜想的情况)。
2.有序猜:出示表格四个组,同桌合作从四个方向猜。
左起,右起,中间靠左,中间靠右开始猜。
3.发现特殊值,渗透极限逼近思想。
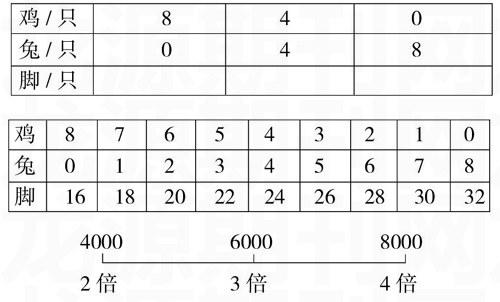
(1)由四种猜法,得一完整表格。(课件出示)
(2)认真观察,从表格中你能不能发现“什么情况下,鸡的只数猜多点,什么情况下,兔的只数猜多点?”(学生独立思考)
(3)需要帮助吗?课件提示:(脚数16,头数8,16是8的2
倍)
(4)再观察,你发现什么?(小组交流)
(5)越靠近2倍,鸡的只数和兔子只数有什么变化?越靠近4倍呢?
(6)现在让你猜兔子和鸡的只数,你会怎么猜?
4.尝试解决例题,并说说你的想法。
片段反思:
教学时,让学生经历尝试、有序列举(填表)、调整,进一步培养了学生有序思考的习惯。通过观察表格,适时地抛出了问题:“什么情况下,鸡的只数猜多点,什么情况下,兔的只数猜多点?”引发学生的认知冲突,突显学生的深刻思考,引导发现特殊值“当兔的只数是0只,全部是鸡时,脚的只数是头数的2倍。当鸡的只数是0时,也就全是兔子,脚的只数是头数的4倍。”探索出:“如果脚的只数越靠近头数的2倍,鸡的只数猜多一点,如果脚的只数越靠近头数的4倍,兔的只数猜多一点。越靠近2倍,鸡的只数越多,越靠近4倍兔子的只数越多,等于2倍,全是鸡,等于4倍全是兔子。”在学生能有序思考基础上,对特殊值进行合理推理,渗透极限逼近思想,探索猜测方向,优化尝试法,产生新的解题策略,渗透假设法的体验。
策略思考:
通过渗透极限逼近的思想,对尝试法进行优化,使学生对尝试的起点有了感性认识,应用这一策略解决问题的几点思考。
1.一一列举法,是一种重要的解题策略,有美中不足。解决“鸡兔问题”中,通过发现尝试起点的规律,可以弥补这一不足。并且学生如果应用假设法解题,此方法也可作为检验答案的依据,锻炼学生推理能力,估算能力。
2.当数据太大,猜测更有难度时,可通过估算,尝试用线段点画出2倍、4倍(端点),3倍(中点)。再取中,或靠左,或靠右,进行尝试猜测,或跳跃式猜测,与列表法有机结合。
例:文化宫电影院有座位2000个,前排每张4元,后排每张2元,前排和后排总价6800元。问该影院前座和后座各有多少个?
6800比6000多,可猜后排多一些,再跳跃式调整。
3.当“脚数”发生变化时,随着“脚数”的变化,调整倍数关系。
例:(P116练习题3)盒子里有大小两种钢珠,共30个,共重266g,已知大钢珠每个11g,小钢珠每个7g。盒中大钢珠、小钢珠各有几个?倍数由鸡兔的2倍、4倍,调整为7倍、11倍。
4.如果已知总脚数差,把问题极端化,使得脚数差最大,通过交换,每换一次,总脚数差减少“2+4”脚数只。
例:鸡兔共有一百只,鸡比兔少70条腿。问鸡兔各有几只?
假设100只全是兔子,则一共有400只脚,鸡有0只,脚数差是400。实际上鸡比兔少70只,两者之间就相差400-70=330只,如果用一只鸡去换一只兔子,每换一次的差就较少6只(注意不是2只),因此需换330÷6=55只,既有55只鸡。
定位于教学多种方法解决鸡兔问题策略,并对尝试列表法进行优化,通过引导发现特殊值,渗透极限逼近思想,寻找尝试规律,培养了学生对尝试起点的敏感性——本质上是对数据的敏感性,并不是为了拔高教学要求,而是将学生可接受的水平结合起来,培养学生推理和探究能力,挖掘并提升问题的教育价值。