基于单调链和STR树的简单要素模型多边形叠置分析算法

陈占龙,吴信才,吴 亮

1.中国地质大学信息工程学院,湖北武汉430075;2.教育部地理信息系统软件开发及应用工程中心,湖北武汉430074

基于单调链和STR树的简单要素模型多边形叠置分析算法

陈占龙1,2,吴信才1,吴 亮1

1.中国地质大学信息工程学院,湖北武汉430075;2.教育部地理信息系统软件开发及应用工程中心,湖北武汉430074

针对简单要素类叠置分析的特点,利用STR(sort-tile-recursive)树索引改进算法能够将尽量多的多边形节点存储在STR树的叶节点中,减少在空间数据库中检索多边形时的磁盘读取次数。算法对多边形边界进行关于坐标轴的单调链分割,并在多边形求交过程中引入平面图的概念,利用平面图元素与各个多边形的拓扑关系来组织叠加后的多边形。该算法能有效减少求交点的时间,在线段求交中加入对连续出入点特殊数据的处理。同时该算法使用单调链减少多边形求交过程的比较次数,与其他使用双链表或单链表的算法相比具有占用空间少及处理速度快的特点。

简单要素模型;单调链;STR树;平面图;空间叠置

1 引 言

矢量图形叠加算法是 GIS空间分析中各种功能的基础。自从1999年OGC提出简单要素模型以来,在当今各主流地理信息软件中,大部分都引入了不维护拓扑信息的数据模型,如ArcGIS中的shapefile数据格式和Map GIS 7.0简单要素类模型等。拓扑模型的矢量叠置分析要求在操作前每一层都是平面增强的,即已经建立了完整的拓扑关系,操作后的结果也是平面增强的[1]。因此,在拓扑模型的叠置分析中,如果叠置前数据层中的数据无完整的拓扑关系,则应首先建立完整的拓扑关系。当数据量过大时,构建拓扑关系的操作需要较多时间,且新数据层中的拓扑关系并不为用户所关心。矢量数据的空间叠置分析能够生成用户感兴趣的新数据层。如果能够将复杂要素模型中的分析功能在简单要素模型下实现,则可免除构建数据拓扑关系这一约束条件,使操作更简单快捷。因无需构建全局拓扑信息,处理速度将比原来的复杂要素模型分析更快[2]。

简单数据模型的叠置分析的核心算法思想是任意多边形裁剪,文献[3]中介绍了基于拓扑模型和简单数据模型的两类算法,比较了两者的优劣并提出可实际应用的基于交点搜索的多边形叠加分析算法。现有的多边形裁剪算法或者局限于解决某类多边形,或者算法结构复杂、时间消耗大,如Sutherl-Hodgeman、梁-Barsky、NLN算法要求裁剪多边形是凸多边形[4-6]。而在GIS的矢量数据的实际应用中,只有对于一般多边形的裁剪才有普遍意义。在一般多边形的裁剪算法中,普遍认为只有Weiler算法和近年出现的Vatti算法及 Greiner-Hormann算法可以在合理的时间内处理一般的情况[8]。在文献[8]中,刘勇奎等提出用单线性链表数据结构的一般多边形的裁剪算法并给出与Vatti算法及Greiner-Hormann算法的比较结果。

本文中提出的算法首先采用单调链算法对输入的多边形进行单调处理以减少多边形比较的次数,然后计算两个多边形的交点,同时将交点插入到相对应的多边形中,该算法引入平面图的概念,通过计算各个平面图元素相对于两个多边形的拓扑关系来得到形成结果多边形的各个平面图元素,最后形成结果多边形。该算法没有运用传统的引入、引出交点交替配对的生成原则进行结果多边形的构建,这样做的好处是简化实现的过程和对异常交点的处理。最后引入STR树空间索引的空间数据高效存取机制,对算法进行改进,进一步提高运算速度。实践结果表明,该算法快速、有效,具有较强的应用价值。

2 相关概念

2.1 平面图与拓扑位置

平面图由一系列的平面图构成元素组成。平面图构成元素主要包括节点(nodes)、边(edges)和有向边(directed edges)。节点记录该节点的位置以及在该节点处的有向边的集合,边则记录组成多边形的边界的坐标串的结构,该结构还是正反两个有向边的组合,有向边记录了由边结构的坐标串形成的顺时针和逆时针的两个方向边。在本文介绍的算法中,参与运算的两个任意多边形通过其记录的坐标串组成两个平面图。拓扑位置是指两个平面图的各个平面图构成元素与这两个平面图的位置关系。各个平面图构成元素中记录了其与两个平面图的拓扑位置关系,拓扑位置的属性是由三元组〈on,left,right〉组成,on表示平面图元素是在(on)平面图的什么位置,left表示该平面图元素的左边是平面图的什么位置, right表示该平面图元素的右边是平面图的什么位置。拓扑相对位置的值由三元组〈interior, boundary,exterior〉组成,分别记录了该元素是在平面图的里面、边界和外部。本算法正是利用这些拓扑位置关系,建立拓扑规则,从候选边集合中找到构成结果多边形的边,从而形成结果平面图,最终形成结果多边形。

例如,对于如图1所示的两个多边形 A和B,其中多边形 A(A1,A2,…,A5)与 B(B1,B2,…,B4)相交于点 I1、I2、…、I4。多边形A和B分别组成平面图 P1和 P2,其中 P1由多边形的 A的边界(A1,A2,…,A5)构成的边组成,P2由多边形的B的边界(B1,B2,…,B4)构成的边组成。多边形A和多边形B的交点I1、I2、…、I4将多边形A和B的边界分割,组成结果多边形的候选集。关于候选集的计算在后面详细介绍。如图1,候选集由 E1、E2、…、E5组成,其中 E1由点 I4、A1、A2和 I1组成,E2由点 I1、A3和 I2组成,以此类推。由上述对拓扑位置概念的定义,在图1中, E1相对于平面图 P1的表达式 E1(P1,on)= boundary表示 E1在平面图 P1的边界上; E1(P1,left)=exterior表示 E1边的左边是平面图 P1的外部;E1(P1,right)=interior,表示 E1边的右边是平面图 P1的内部;E1(P2,left)= exterior和 E1(P2,right)=exterior表示无论是E1的左边还是 E1的右边都在平面图 P2的外部,因此 E1(P2,on)没有意义,以此类推。对于 E2,其拓扑位置如下式所示

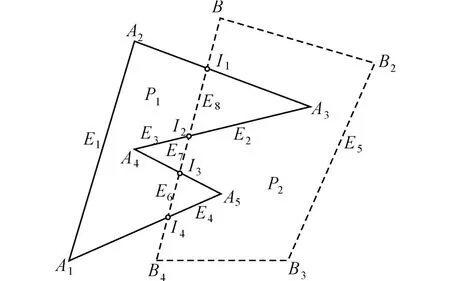
图1 多边形平面图示例Fig.1 The plane graph of two polygons

2.2 STR Tree和单调链

Leutenegger等在 1997年提出一种 STR (sort-tile-recursive)压缩算法[9]。该算法易于实现。其基本思想为:假设在2维空间中有N个矩形,M是R树结点的最大容量,用矩形中心点的x坐标对数据矩形排序,用S= N/M个垂直切片切割数据空间,使得每个切片包含足够的多边形从而压缩个节点。其中每个切片具有S个结点和S×M个矩形(最后一个切片会少于S×M个矩形)。然后在每一个垂直切片中,用矩形中心点的y坐标对数据矩形排序,每M个矩形一组依次压入结点,自下而上一次一层递归生成整个R树。

由STR的压缩算法可知,在压缩R树中的每一层中,除了最后一个结点可能不满外,其他所有结点都是满的。因此可以获得几乎100%的空间利用率。这种索引树的方式正好满足简单要素类叠加分析中一次建立索引的需求,即一次建立,不需要动态构建索引树,而经典的R树大都是动态建立,空间利用率不高。

链(或称多边形链)C=(u1,u2,…,un)是一个具有顶点集{u1,…,un}和边集n-1}的平面图。若正交于 l的一条直线恰好交C于一点,则称折线 C关于直线l是单调的,如图2。下面介绍单调链的概念。将折线C上的各个顶点ui投影到直线l上,得到投影点 l(ui),若l(ui)(i≠0)距离 l(u0)以递增的顺序出现,则称折线C关于直线l单调[10]。单调链主要有以下两个性质:①不相交性质,属于同一个单调链的各个线段不会相交;②端点组成外包矩形性质,在一个单调链中连续的线段的外包矩形为这些线段组成的子单调链的端点组成的外包矩形。图2是单调链的定义图,图3是多边形分割的各个单调链的示意图。

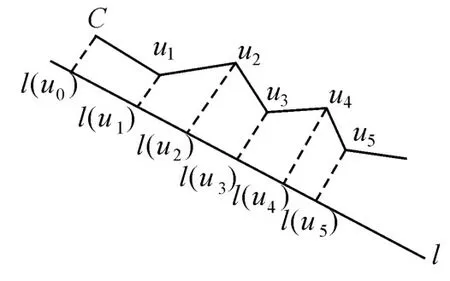
图2 C对l的单调链Fig.2 Monotone chain

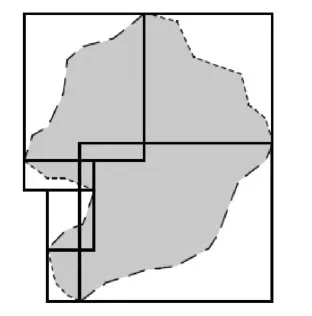
图3 多边形的单调链[11]Fig.3 The monotone chains of polygons

3 算法的数据结构

多边形相交算法需要适当的数据结构来存储多边形及交点,并能够在其上进行正确的操作。现介绍本算法中用到的数据结构。本算法采用基于点坐标存储的方法来存储区、线的坐标序列,多边形的边界用点坐标串表示,如图4表示的是两个多边形及其交点的存储结构。polygon1由坐标串v1,v2,…,v8组成,且该多边形根据多边形单调链分割算法把多边形边界分割为 mc1,mc2,…,mc4,其中单调链只是记录了坐标序列的指针以节省存储空间。

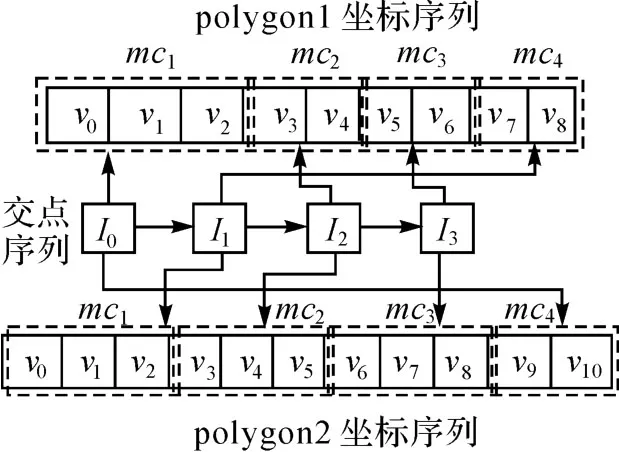
图4 多边形及其交点数据链图Fig.4 The data structure of intersection point and polygons

值得一提的是,该算法的交点数据结构中并没有记录经典算法中的出点和入点等数据结构,只是记录了该交点在两个多边形边界坐标串的插入位置,以便生成结果多边形的候选边集合。

与经典的双向链表结构 (如 Greiner-Hormann算法)相比,该存储结构不仅由于少用了一个指针域而节省了存储空间,而且还进一步降低了数据结构的复杂性。该算法中交点存储结构无需修改双向链表或者单链表的指针,因此对该结构的操作变得简单并且更加节省计算时间。

4 算法的设计与实现

该算法主要分为以下四个阶段:第一个阶段计算两个多边形的交点,并根据交点计算相交结果多边形的候选边(edges)集;第二阶段计算候选边集中各个边相对于两个多边形的拓扑位置关系;第三阶段根据第二阶段计算的两个多边形的拓扑位置关系来从候选边集中挑选组成结果多边形的边,最终生成结果多边形;第四阶段结合简单要素类区多边形叠加分析的特点,利用STR树索引进行大规模计算,用来提高大数据量多边形叠加分析运算的效率。

4.1 候选边集的计算

在候选边集的计算过程中,首先将参与叠加运算的多边形A和多边形B的边界分割成各个单调链。如图5,多边形 A由坐标串{v1,v2,…, v21}和{v22,v2,…,v31}组成,其中 Edge1{v1,v2,…,v21}为多边形 A的外圈,Edge2{v22,v2,…, v31}为多边形 A的内圈。单调链的计算过程如下:以多边形A的外圈为例,首先计算 v1v2所在的象限,象限的计算是根据向量v1v2与 x轴的角度确定;然后计算v2v3的象限,如果相同则继续比较,如果不相同则要进行处理,如v3v4开始与计算的象限不同,则{v1,v2,v3}组成一个单调链 mc1,然后从 v3开始计算,可以得到{v3,v2,…,v8}组成一个单调链 mc2,在单调链的存储结构只存储了起始终止顶点号,并没有存储实际的坐标值以节省存储空间。在求交点的过程中,参考文献[12],利用上述方法求得的各个单调链,根据单调链的两点基本特性,在扫描线算法中,仅将单调链的左端点定义为事件点,参与排序的单元的数目就是实际单调链的条数。这里使用堆排序方法对单调链时间进行排序。连接线段集分解为单调链后,几何中元的数目会极大地减少,提高了线段求交点是速度。利用上述求交点的算法可以求得多边形 A和多边形B的交点{I1,I2,I3,I4,I5,I6},如图5所示,计算出的交点则将多边形A和多边形B的边界分割成各个离散的边。如表1所示。

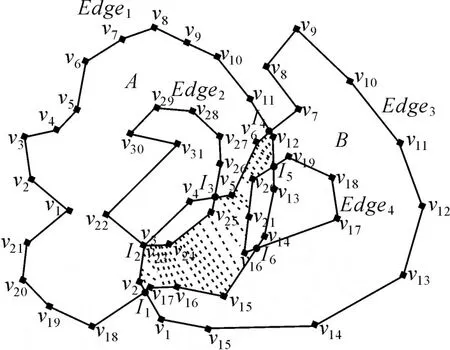
图5 多边形A与B相交示意图Fig.5 The figure of intersection of polygonAand polygonB

表1 离散子边表Tab.1 The table of sub edges

在子边(subEdgei)中的数据结构中,只存储了其父亲边的指针和组成该边的起始顶点号和交点号以节省存储空间,这些边组成了结果多边形边的候选集。

4.2 候选边拓扑位置的计算

由平面图及拓扑位置的定义,以图5为例介绍上一节计算出的各个子边(S ubEdgei)的拓扑位置的计算过程。该过程主要分为两步。

第一步:计算组成多边形的各个边相对于自己的拓扑位置。例如,计算组成多边形 A的边(Edge1和 Edge2)相对于多边形A的拓扑位置的过程为:假设多边形A的外圈Edge1以顺时针方向存储坐标点序列,多边形A的内圈Edge2以逆时针方向存储坐标点序列,则可以判断多边形A的边(Edge1和 Edge2)的拓扑位置为

同理可以计算多边形B的两个圈边界的拓扑位置为

第二步:计算各个子边的拓扑位置。子边(subEdgei)的拓扑位置首先继承了其父类边的拓扑位置,然后计算该子边相对于另外一个多边形O(Other)的拓扑位置。其计算过程如下:因该子边没有组成多边形O,所以其拓扑位置的取值不可能是boundary,所以只需取子边中的一顶点v,判断该顶点v是在多边形O的内部和外部即可。以子边(subEdge2)为例,因其父亲边为 Edge1,所以其继承了 Edge1相对于 A的拓扑位置,即: subEdge2(A,on)=boundary,subEdge2(A,left) =exterior,subEdge2(A,right)=interior,只需计算子边(subEdge2)相对于 B的拓扑位置即可。取子边(subEdge2)的顶点v12,根据点与多边形的位置关系的经典算法可以判断,v12在多边形B的内部(interior)。因此可以判断子边(subEdge2)的对于B的拓扑位置为:subEdge2(B,on)=interior,subEdge2(B,left)=interior,subEdge2(B, right)=interior。同理计算其他子边的拓扑位置如表2所示。

表2 各子边的topology表Tab.2 The topology of sub edges

表2中,i代表interior;e代表exterior;b代表boundary;“/”符号前面是相对于多边形 A的拓扑位置关系,“/”符号后面是相对于多边形 B的拓扑位置关系,例如subEdge1(on)=b/e表示subEdge1对于多边形A是在A的边界(b)上,对于多边形B是在多边形B的外部(e)。

4.3 结果多边形的计算

在完成以上的计算后,计算结果多边形就比较容易了。根据叠加操作的类型从表3的候选集中挑出子边组成结果集。挑选的规则如表3所示。

由以上定义的规则,以多边形交操作为例,参考表3中计算出的拓扑位置关系,可以得出组成结果多边形子边集合为{subEdge2,subEdge4, subEdge7,subEdge11,S ubEdge15,S ubEdge17},如图5阴影部分所示。

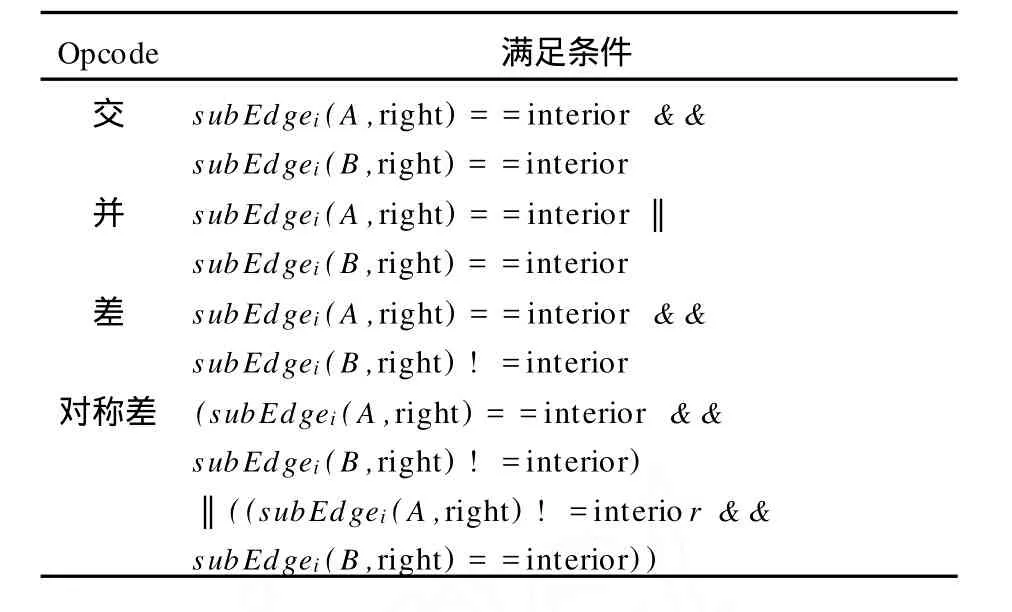
表3 叠置操作规则表Tab.3 The operation rule table of overlay

4.4 利用STR树索引进行计算

如果考虑利用STR树对整个图层的图元创建索引,即将图层中的所有图元的MBR按STR树的层次形式来组织[13]。这样,就可以通过STR树本身的高效访问机制,在叠加操作之前,对空间数据进行快速查询和筛选,减少参与叠加处理的图元数目,从而提高空间操作的效率。

具体操作步骤如下:

1.比较叠加分析操作两个图层的图元数目,对图元较多的那个图层创建STR树索引。

2.遍历图元较少的图层中的每个图元,并用该图元的MBR作为查询窗口矩形,对索引图层进行STR树窗口区域查询,这样,利用STR树索引快速地查找出仅与查询窗口相关(相交或包含)的索引图层中的图元。

3.将作为查询窗口的图元(叠加图元)与查找出来的这些相对较少的图元(被叠加图元)进行遍历叠加操作(调用前面介绍的两个多边形叠加算法)。

5 算法分析及试验结果

与经典的算法相比,本算法无需对生成的出点、入点作判断,无需对多边形的各个边界点都实施计算操作以形成结果多边形,只需要从生成的边中根据叠置操作的规则找到形成结果多边形的边。这使得在实际处理异常交点时变得非常简单。

对基于单调链的求交点算法性能分析如下:设平面线段集的线段条数为 n,分解后的单调链条数为m。初次过滤只涉及简单的点在矩形内的判断,只需对每条线段遍历一次即可完成,这一步处理的时间复杂度为O(n)。对单调链分解可以在O(n)时间内完成,然后对单调链进行排序,这一步处理的时间复杂度为O(mlgm)。根据文献[12]中对基于单调链的线求交性能分析,每一次单调链的过滤处理可以在O(milgmi)+O(mi)时间内完成。设一次粗扫描的单调链过滤最多处理M条单调链,整个扫描处理需处理 T条线段,K为整个平面线段集的交点个数,则扫描求交的总时间复杂度的上限可表示为

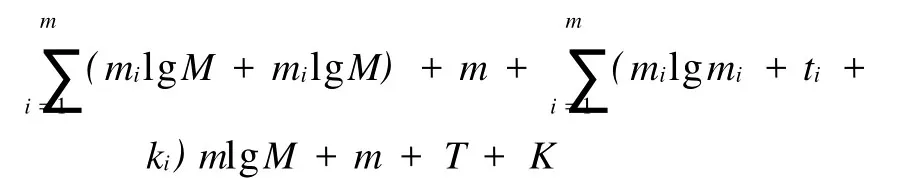
所以扫描求交的时间复杂度为O(mlgM+m+T+ K),相关详细信息请参看文献[12]。

简单要素模型下的多边形叠置分析,其规模是线性增长的,线段求交操作对算法效率的影响最大,本算法通过空间数据索引和空间数据内存管理调度机制保障算法的效率。拓扑模型下的叠置分析除了线段求交外,还要重新构建拓扑关系,因此当线段求交效率接近时,拓扑模型的叠置效率略差于简单要素模型。本文以MapGIS 7.0平台为基础,按照算法的设计思想实现了简单要素模类的叠置分析,在对实际数据的处理中得到了较好的应用,并与拓扑模型下的叠置分析进行对比试验。实验的结果分析如表4所示。

表4 各个数据量级别下该算法与要素模型的执行时间比较T ab.4 The comparison of the simple data model and the topological data mode

6 结束语

本文的多边形叠置算法不仅适用于凹多边形,也适用于带孔洞的多边形,不仅可以求多边形的“交”(多边形裁剪),还能够求多边形的“并”和“差”。该算法无需对生成的交点进行出点和入点的判断,无需把所有的两个多边形的各个边界点都读出来进行计算来形成结果多边形,只需要从生成的候选边中找到结果边生成结果多边形,因此该算法比同类算法实现简单。本文还提出一些新的技术和方法如利用单调链求交点和利用拓扑位置计算结果多边形等。最后,以MapGIS 7.0平台为基础,将该算法与拓扑模型的算法进行比较,实验结果表明该算法性能优于其他同类算法。由于简单要素类模型下的各个多边形之间没有拓扑关系,因此该模型较拓扑模型更易于实现叠置分析算子的并行化操作[2]。大规模数据量下的并行化操作的实现将进一步提高简单要素模型下叠置运算的效率。将该算法进行并行化处理将是作者今后研究的方向。

[1] WU Xincai.Geographic Information System Principles,Methods and Applications[M].Beijing:Electronics Industry Press, 2002.(吴信才.地理信息系统原理、方法及应用[M].北京:电子工业出版社,2002.)

[2] XIE Zhong,YE Zi,WU Liang.Polygon Overlay Analysis Algorithm Using the Simple Data Model[J].Geography and Geo-Information Science,2007,23(3):19-23.(谢忠,叶梓,吴亮.简单要素模型下的多边形叠置分析算法[J].地理与地理信息科学,2007,23(3):19-23.)

[3] XUE Sheng,PAN Mao,W ANG Yong.Research of the Algorithms of Polygon’s Overlay[J].Computer Engineering and Applications,2003(2):57-59.(薛胜,潘懋,王勇.多边形叠置分析算法研究[J].计算机工程与应用,2003(2):57-59.)

[4] SUTHERLAND I E,HODGEMAN G W.Reentrant Polygon Clipping[J].Communications of the ACM,1974,17(1): 32-42.

[5] LIANG Y,BARSKY B A.An Analysis and Algorithm for Polygon Clipping[J].Communications of the ACM,1983,26 (11):868-877.

[6] FOLEYJ D,DAM A,FEINER S K,et al.Computer Graphics, Principles and Practice[M]. Boston: Addison-Wesley,1990.

[7] MAILLOT P G.A New,Fast Method for 2D Polygon Clipping:Analysis and Software Implementation[J].ACM Transactions on Graphics,1992,11(3):276-290.

[8] LIU Yongkui,GAO Yun,HUANG Youqun.An Efficient Algorithmfor Polygon Clipping[J].Journal of Software,2004,14 (4):845-856.(刘勇奎,高云,黄有群.一个有效的多边形裁剪算法[J].软件学报,2004,14(4):845-856.)

[9] LEUTENEGGER S,EDGINGTON J M,LOPEZ M A.STR: A Simple and Efficient Algorithm for Rtree Packing[C]∥Proceedings of the 13th IEEE ICDE.Birmingham:IEEE Computer Society,1997:497-506.

[10] ZHOU Peide.Computational Geometry[M].Beijing:Tsinghua University Press,2000.(周培德.计算几何[M].北京:清华大学出版社,2000.)

[11] VIVID.VIVID Solutions:J TS T opology Suite Technical Specifications[EB/OL].[2008-05-12].http:∥www.vividsolutions.com,2003.

[12] YANG Chongjun,REN Yingchao,LI Jinping.Red-Blue Sweep Line Algorithm Based on Monotone Chains for Connected Line Segment Intersection Problems[J].Geomatics and Information Science of Wuhan University,2006,31(9): 835-838.(杨崇俊,任应超,李津平.基于单调链的Red_ Blue扫描线求交算法[J].武汉大学学报:信息科学版, 2006,31(9):835-838.)

[13] DONG Peng,YANG Chongjun,LIU Donglin,et al.A Dual Loop Map Overlay Algorithm Based on R+Tree[J].Journal of Image and Graphics,2003,6(8A):703-710.(董鹏,杨崇俊,刘冬林,等.基于R+树的地图叠加分析双重循环算法[J].中国图象图形学报,2003,6(8A):703-710.)

Polygon Overlay Analysis Algorithm Based on Monotone Chain and STR Tree in the Simple Feature Mode

CHEN Zhanlong1,2,WU Xincai1,WU Liang1
1.Faculty of Information Engineering,China University of Geosciences,Wuhan 430075,China;2.China GIS Software Research and Application Engineering Center of the Ministry of Education,Wuhan 430074,China

An improved overlay analysis algorithm based on monotone chain and STR(sort-tile-recursive)tree index is introduced.The algorithm can save the time for vertex listing and intersection point computation,also the memory space.Making full use of the function of overlay analysis for simple features,as many as possible nodes of the polygon can be filled in the STR tree index structure.The algorithm reduces the access times when querying the polygons in the spatial database.The algorithm splits the edges in the polygon by the monotone chain algorithm to compute the intersect point firstly.Secondly,the concept of plane graph is used in this algorithm.The algorithm organizes the result polygons by computing the topology location between the plane graph components of the two polygons.It has been reduced the computing intersect point time and emphasizes on the solution of the problem of the entry point or exit-point successive and the alternative searching of the intersected polygon.

simple feature model;monotone chain;STR tree;plane graph;polygon intersection

CHEN Zhanlong(1980—),male,PhD,majors in theory and method of GIS.

1001-1595(2010)01-0102-07

P208

A

国家863计划(2006AA12Z218);国家自然科学基金(40771165);中央高校基本科研业务费专项资金(CUG L090251)

(责任编辑:丛树平)

2008-07-22

2009-07-06

陈占龙(1980—),男,博士,研究方向为地理信息系统研究与应用。

E-mail:chenzhanlong2005@126.com