用“五问法”分析几何题

2009-11-17刘化雷

中国校外教育(下旬) 2009年14期

刘化雷

【摘要】本文介绍一种对初学几何者简单易学、行之有效的分析方法——“五问法”。所谓“五问”是指:一问已知什么,二问求什么,三问由已知能得到什么,四问要得结果需知什么,五问收获了什么。

【关键词】五问法几何题分析方法

初中生学几何,难在入门;入门难,难在对题意的理解;理解难,难在缺少正确的方法。新课程标准降低了对欧几里德几何学的要求,对初学者我们不必对其逻辑思维的严密性做太高的要求,而培养正确的理解题意、分析解题思路的方法才是当务之急。方法对路了,逻辑性就培养出来了,这是水到渠成的事儿。

那么怎样培养学生正确的理解题意、分析解题思路的方法呢?笔者在多年的教学实践中,总结出了简单易学、行之有效的“五问法”分析几何题的方法。所谓“五问”是指:一问已知什么,二问求什么,三问由已知能得到什么,四问要得结果需知什么,五问收获了什么。下面,以一道几何题为例,详细解释“五问法”的操作步骤,题目为:“如图1,CD=BE,DG⊥BC,EF⊥BC,垂足分别为G,F,且DG=EF.判断下列结论是否正确,并说明理由:(1)BG=CF;(2)BD=CE.”

一问已知什么,就是要求学生结合图形认真审题读懂题意,将题目的“已知”与图形中的信息“对号入座”。在教学实践中可以发现,大部分对几何题的分析能力较差的学生都是没有过好审题这一关:要么不知题目的已知条件,要么题意与图形相脱离。当学生遇到不会做的题目过来请教老师时,经常上来就问:“老师,这道题目怎么解?”我的习惯是立即反问一句:“题目已知哪些条件?”并要求学生结合图形把已知条件说出来给我听,同时要求他(她)在图形上标注必要的符号。这样做的目的有两个:一是检查一下这位学生认真审题了没有,二是让学生重温一下题目的情景,以利于下面的分析。如例题中,我要求学生首先读出题目的“已知”,并在图中加上必要的记号,如CD=BE,则在线段CD、BE上各加相同的短横;DG=EF,则在线段DG、EF上各加相同的双短横以区别于CD、BE上的短横;DG⊥BC,EF⊥BC,则分别标出垂足(见图2)。标注完毕,要求学生脱离题目只看图形,完整地说出题目的“已知”。这样,学生对题目的已知条件做到了熟知于心,印象于形,接下来的分析才会相对严密,而不是丢三落四。

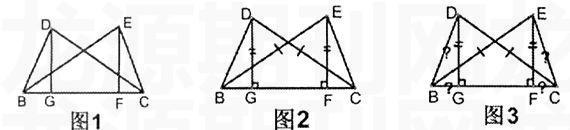
二问求什么,求什么当然很重要,要不然连现在该干什么都不知道了,还谈何解题呀?话虽如此,初学几何者弄不清题目要求他干什么的大有人在。当然,“求什么”不仅是文字上的理解,还要知道“求什么”在图形中的对应信息,我通常要求学生把“求什么”在图形中用“?”予以标注,如本题是要求求证(说理)(1)BG=CF;(2)BD=CE,学生只需在线段BG、CF、BD、CE上分别标上“?”。

三问由已知能得到什么,这是分析几何题的关键。学生每得到一个已知条件,大脑中能否快速地、准确地、系统地、完整地闪现出与之相关的数学信息就是其数学知识积累程度的具体体现。这就需要学生注意对数学知识的日积月累,也需要教师经常帮助学生系统地整理数学知识。分析题目时,学生把相关的信息在图形中得以体现,并在草稿纸中做好相关记录。其实这样做就是在为综合法解题作铺垫。例题中,学生容易由图2中的已知信息得出Rt△CDG≌Rt△BEF(HL),同时进一步得到全等三角形的对应元素相等,如CG=BF、∠DCB=∠EBC等。

四问要得结果需知什么,与“三问”类似,要得结果需知道什么就是在为分析法解题作铺垫。学生只有懂得去分析“欲知结果,必先如何”,才能与由已知得到的信息挂上钩,让思路连通,使题目得解。更是要知道为了得到所求的内容,需要先知道什么条件,即执果索因,这就要求学生对所学的几何定理有比较全面的理解。学生要结合已知与求证的内容做合理联想,如:“以前做过或见过类似的问题吗?当时是怎样想的?题中的一部分(条件或结论或式子或图形)以前见过吗?在什么问题中见过?解这类问题通常有几种方法?哪种方法较简便?与这个问题有关的知识(基本概念、定理、公式等)有哪些?”等等。

本题中,学生由图3可发现,要说明BG=CF,只需要知道BF=CG,因为BG=BC-CG,CF=BC-BF,这恰与前面分析得到的结论BF=CG相吻合,得证;学生或者会想到要说明BG=CF,只需证明Rt△BDG≌Rt△CEF,但是显然缺少使之全等的直接条件,两者相比较,选择第一种方案比较合适。第二问要证明BD=CE,需知什么?学生通过对图3的观察分析,可能会发现可以证明Rt△BDG≌Rt△CEF或者△BDC≌△CEB,与前面的分析和证明结果相结合,这两种途径都容易获得成功。

五问收获了什么,一般地,把前面的四问解决好,几何题就迎刃而解了,为什么还要设置这第五问呢?这其实是一个解题反思过程,是数学解题的“第二过程”。如果我们把暴露结论的发现过程、暴露思路的探求过程、暴露方法的提炼过程称为“第一过程”,那么,在暴露结论发现、思路探求的基础上,继续反思数学解题的过程称为“第二过程”。这“就象黑夜摸进一座大楼的新房间,撞在墙上、碰倒桌椅、甚至摔跤都是有可能的,但进去之后,就不要老是在黑房间里摸索了,就应该拉开黑房间的电灯,看清房间的结构并反思当初的摸索”。学生在解完几何题后要及时反思解题的结论发现过程、思路的探求过程、方法的提炼过程并总结自己的收获以发展自己的数学思维。同时,学会回头看对培养学生良好的学习、做事习惯很有好处,是促使学生进步的重要举措。

下面,把用“五问法”解几何题中这“五问”之间的联系用框架图表示出来:

其中“桥——联系”是指当由已知不能直接得到所求的结果,由所要求证的结果不能直接找到已知条件时产生的一些中间过渡性结论的总称,它在几何题的分析中起承上启下的作用,如例题中的中间结论BF=CG、Rt△BDG≌Rt△CEF等。